多传感器信息融合的典型应用_多传感器最优信息融合卡尔曼滤波器

摘要：

本文提出了一种新的基于线性最小方差意义的矩阵加权的多传感器最优信息融合准则，它等效于正态分布假设下的最大似然融合准则。基于该最优融合准则，针对具有多个传感器和相关噪声的离散时间线性随机控制系统，给出了一种具有两层融合结构的通用多传感器最优信息融合分散卡尔曼滤波器。第一融合层具有网状平行结构，以在每个时间步长确定每对无故障传感器之间的交叉协方差。第二融合层是确定最佳融合矩阵权重并获得最佳融合滤波器的融合中心。与集中滤波器进行比较，结果表明，在所有传感器均无故障的情况下，融合滤波器的计算量减轻了，融合滤波器的精度也比集中滤波器的精度低；但是当某些传感器出现故障时，融合滤波器具有容错性和鲁棒性。此外，融合滤波器的精度高于每个局部滤波器的精度。将其应用于具有三个传感器的雷达跟踪系统证明了其有效性。

关键词：多传感器信息融合；线性最小方差；最大似然;最优信息融合卡尔曼滤波器；容错能力；雷达追踪系统

Multi-sensor optimal information fusion Kalman filter

Shu-LiSun∗,Zi-LiDeng 2004

Department of Automation, Heilongjiang University

黑龙江大学自动化系

1.简介

信息融合卡尔曼滤波理论已经被研究并广泛应用于飞机，轮船，汽车和机器人等机动目标的集成导航系统中。当多个传感器测量同一随机系统的状态时，通常我们有两种不同类型的方法 处理测量的传感器数据。 第一种方法是集中式过滤器（Willner,Chang,＆Dunn,1976）,在该过滤器中，所有测得的传感器数据都被传送到中央站点进行处理。 此方法的优点是它所涉及的信息丢失最少。 但是，由于过滤器过载而导致的数据超出其处理能力，可能导致严重的计算开销。因此，当出现严重的数据故障时，整个集中式过滤器可能不可靠或准确性和稳定性较差。第二种方法是分散滤波器，其中来自局部估计器的信息可以根据某些信息融合准则产生全局最优或次优状态估计。该方法的优点在于，融合中心的通信和存储空间的要求得到了拓宽，并且并行结构将导致输入数据速率的提高。此外，分散可轻松实现故障检测和隔离。然而，当没有数据故障时，分散滤波器的精度通常低于集中滤波器的精度。卡尔曼滤波器的各种分散和并行版本及其应用已有报道（Kerr,1987;Hashhmipour,Roy,＆Laub,1988）,包括卡尔森的联合平方根滤波器（1990）。但是在某种程度上，他的滤波器具有保守性，因为它使用过程噪声方差矩阵的上限而不是过程噪声方差矩阵本身，并且假定初始估计误差是不相关的。Roy and Iltis（1991）给出了线性线性系统的分散静态滤波器，具有相关的测量噪声。Kim（1994）在正态分布的假设下，基于具有多个传感器的系统的最大似然意义，给出了一个最佳融合滤波器，并假设过程噪声与测量噪声无关。 Saha（1996,1998）讨论了稳态融合问题。 Deng和Qi（2000）给出了一个多传感器融合标准，由标量加权。 但是，局部子系统之间的估计误差不相关的假设与一般情况不符。 Qiang和Harris（2001）讨论了两种测量融合方法的功能等效性，其中第二种方法要求测量矩阵的大小相同。

在本文中，由Kim（1994）提出的在正常密度函数下的最大似然融合准则的结果被重新推导为在线性最小方差意义上由矩阵加权的最优信息融合准则。基于融合准则，具有容错性和鲁棒性的最优信息融合分散滤波器可提供具有多个传感器和相关噪声的离散时变线性随机控制系统。它具有两层融合结构。第一融合层具有网状平行结构，以在每个时间步长确定每对无故障传感器之间的交叉协方差。第二融合层是融合中心，其融合所有局部子系统的估计和方差，以及来自第一融合层的局部子系统之间的交叉协方差，以确定最佳矩阵权重并产生最佳融合滤波器。

2.问题公式化

考虑带有l个传感器的离散时变线性随机控制系统

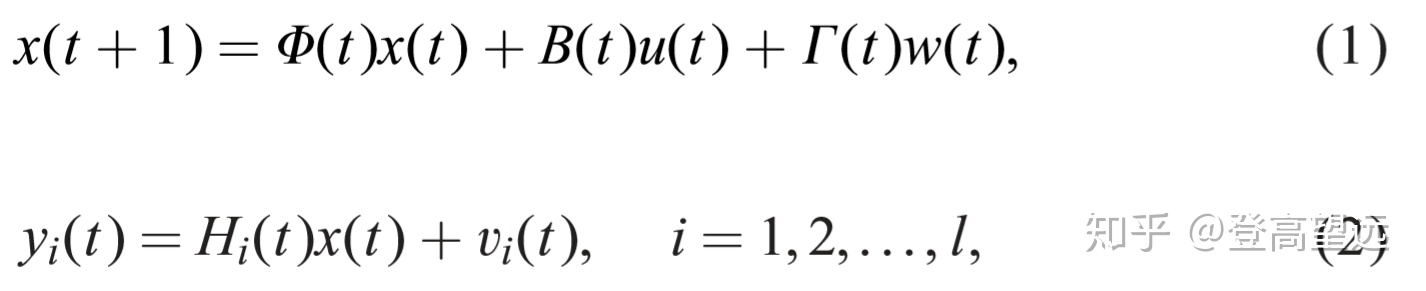
其中

是状态，

是测量值，

是已知的控制输入，

是白噪声，并且

是时变矩阵，且维数兼容。

在下文中，

表示n×n单位矩阵，0表示具有兼容尺寸的零矩阵。

假设1.

和

是相关的白噪声，均值为零，且

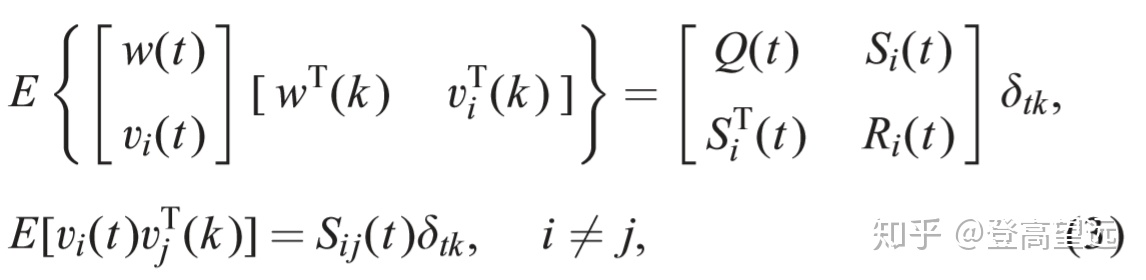
其中符号E表示数学期望，上标T表示转置，

是克罗内克脉冲函数。

假设2.初始状态

与

和

无关，且有

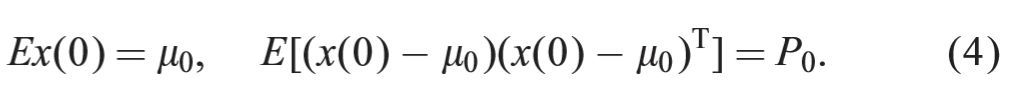
我们的目标是基于测量

来找到状态

的最优（即线性最小方差）信息融合卡尔曼滤波

，它将满足以下性能：

(a)无偏，即

；

(b)最优性，即找到最优矩阵权重

以最小化融合滤波误差方差的迹，即tr[Po(t|t)]=min{tr [P(t|t)]}，其中符号tr表示矩阵的迹，[Po(t|t)]表示具有矩阵权重的最优融合滤波器的方差，P(t|t)表示具有矩阵权重的任意融合滤波器的方差。

3.线性最小方差意义上的最优信息融合准则

1994年，Kim在标准正态分布的假设下提供了最大似然融合准则。在这里，我们将在线性最小方差意义上得出相同的结果，其中避免了正态分布的限制性假设。为简单起见，在以下推导中将时间t删除。

定理1.令

为n维随机向量x的无偏估计量。假设估计误差为

。假设

和

相关，并且方差和交叉协方差矩阵分别由Pii（即Pi）和Pij表示。然后给出具有矩阵权重的最优融合（即线性最小方差）估计

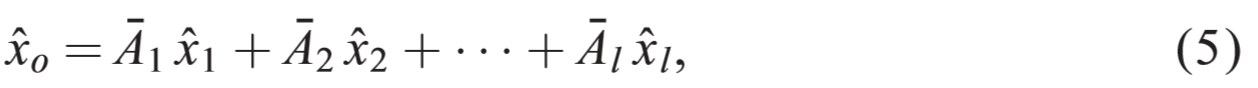
这里的最优矩阵权重

计算为

其中

是nl×nl对称正定矩阵，

和

都是nl×n矩阵。最优信息融合估计量的相应方差由下式计算：

我们有结论：

证明：引入综合无偏估计量

。。。

。。。

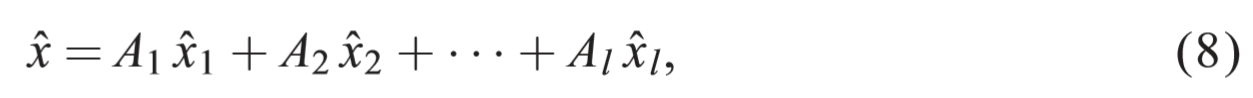
推导结论。

4.具有两层融合结构的最优信息融合分散卡尔曼滤波器

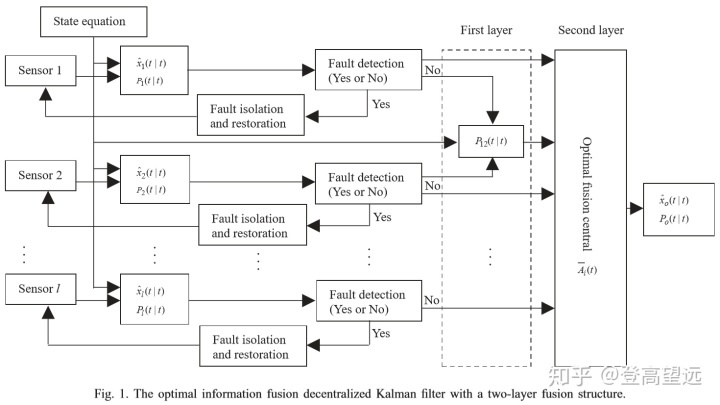
在假设1和2下，具有多个传感器的系统(1)-(2)的第i个局部传感器子系统具有局部最优卡尔曼滤波器（Anderson＆Moore，1979）

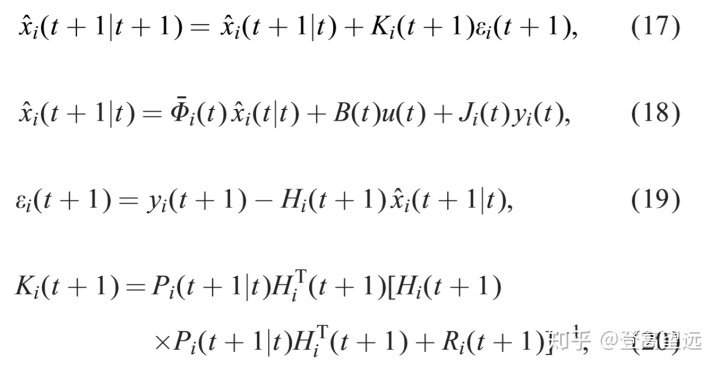
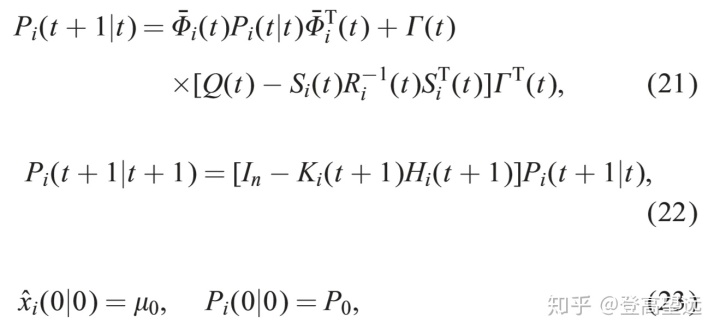
这里

。对于第i个传感器子系统，

,

和

分别是滤波和第一步预测误差方差矩阵，

是滤波增益矩阵，

是新息过程。

由于第i个子系统和第j个子系统的滤波误差是相关的，因此我们有以下定理2。

定理2.在假设1和2下，第i个传感器子系统和第j个传感器子系统之间的局部卡尔曼滤波误差交叉协方差具有以下递归形式：

其中，

是第i个和第j个传感器子系统之间的卡尔曼滤波误差交叉协方差矩阵，以及初始值Pij（0 |0）= P0。

证明：

。。。

。。。

推论1：在定理2中，如果Si（t）= 0，Sij（t）= 0，则交叉协方差Pij（t +1 | t +1）可以简单地由

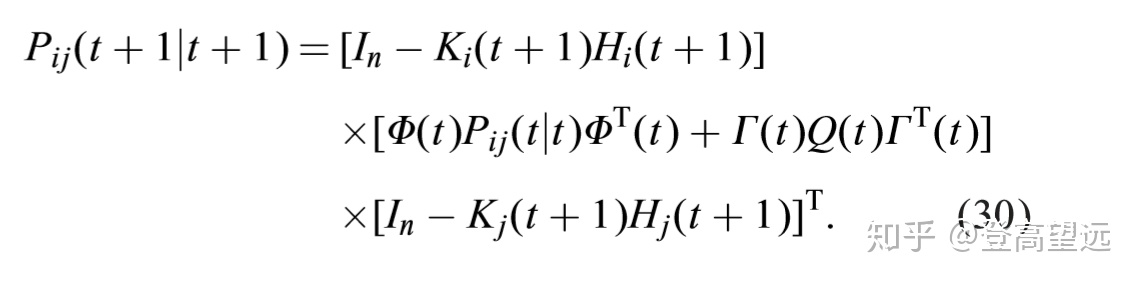
证明：

。。。

。。。

基于定理1和定理2，可以容易得到下面的推论。

推论2：对于假设1和2下的系统(1)-(2)，我们得到最优信息融合分散式卡尔曼滤波器为

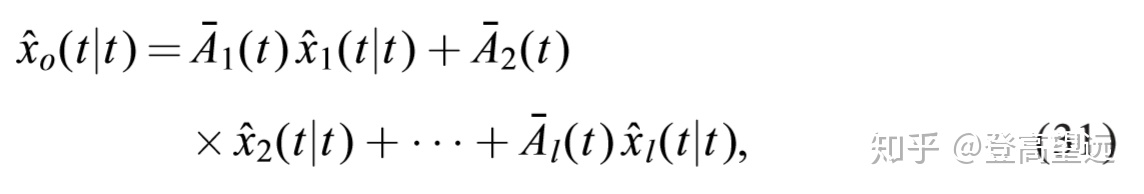
其中，

由式(17)-(23)计算得到；

由式(6)计算得到;

由式(7)计算得到。局部子系统的滤波误差方差

和交叉协方差

分别由式(22)和(24)计算。

证明：

。。。

。。。

5.仿真示例—最优融合分散卡尔曼跟踪滤波器

考虑具有三个传感器的雷达跟踪系统

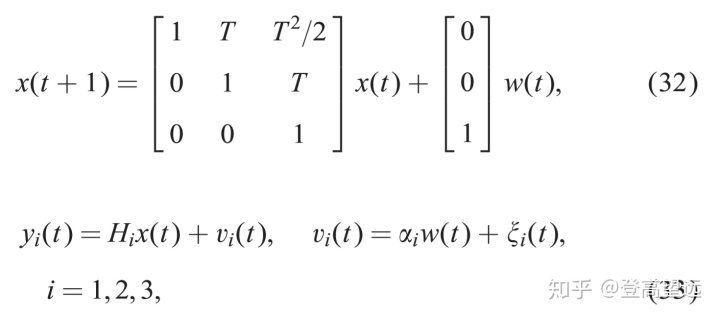
其中，T是采样周期。状态为

，其中

分别是目标在时间t的位置，速度和加速度。

是三个传感器的测量信号，

分别是三个传感器的测量噪声，它们与均值为零且方差为

的高斯白噪声w(t)相关。系数

是常数标量，而

是具有均值为零和方差矩阵

的高斯白噪声，并且与w(t)无关。我们的目的是找到最优的信息融合分散卡尔曼滤波器。

在仿真中，设置

初始值

,我们使用300个样例。

对于每个传感器子系统，分别应用(17)-(23)，我们可以获得局部最优卡尔曼滤波器

和相应的方差

。在第4节应用两级融合结构，我们有最优的信息融合

和相应的方差

。为了与集中滤波器进行比较，还计算了集中滤波器的方差

。我们选择适当的坐标以清楚地显示它们的差异。从图2中我们可以看到，最佳融合分散滤波器的精度高于每个局部滤波器的精度，但是当所有传感器都完好无损时，其精度低于集中滤波器的精度。尽管局部滤波器1和2的精度较低，但分散式过滤器的精度更高，并且接近集中式过滤器。

为了计算融合滤波器的容错性和鲁棒性，我们假设第一个传感器有故障，以使测量方程式为y1(t)= H1x(t)+ v1(t)+ f(t)，其中f(t)满足

;

。f(t)的值表明，第一个传感器出现故障故障值t=100，并在t = 200时恢复。

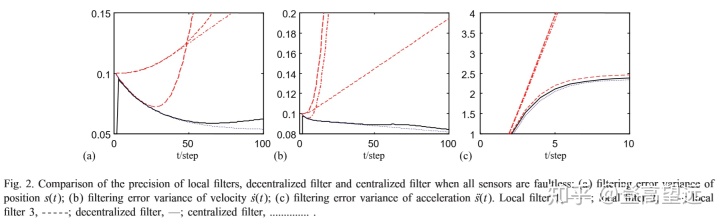
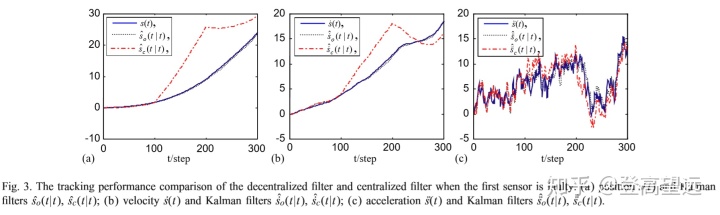
应用第4节中的两层融合结构和WSSR（Willsky，1976）验证，在图3中，融合点用虚线表示，集中点用虚线表示，而实际值则用实线表示。从仿真数据可以看出，由于第一个传感器在

时出现故障，因此集中式滤清器会发散。但是分散的过滤器仍然可以跟踪目标。结果表明，当传感器出现故障时，具有两层融合结构的信息融合分散滤波器具有更好的容错性和鲁棒性。

6.结论

对于Kim（1994）提出的标准正态分布假设下的最大似然融合准则，本文使用拉格朗日乘数法和线性最小方差意义上的新解释给出了新的推导。 基于该融合准则，针对具有多个传感器和相关噪声的离散时变线性随机控制系统，给出了具有两层融合结构的多传感器最优信息融合分散卡尔曼滤波器。 它具有以下属性：

（i）线性最小方差意义上最优融合准则的新推导避免了正态分布的假设（Kim，1994）。

（ii）它可以解决带有多个传感器和相关噪声的系统的最优融合问题。

（iii）对于具有相关噪声的系统，给出了第i个传感器子系统和第j个传感器子系统之间的交叉协方差。

（iv）避免保守地使用过程噪声方差的上限而不是过程噪声方差本身（Carlson，1990）。

（v）当测量矩阵大小不同时，它可以处理融合问题，从而避免将测量矩阵大小限制为相同大小（Qiang＆Harris，2001）。

（vi）避免了来自融合中心的反馈信息的交流。

（vii）给出了具有容错性和鲁棒性的两层融合结构。提出了确定每对传感器之间的交叉协方差的网状并行结构。