正弦定理和余弦定理_正弦定理、余弦定理

1.  正弦定理(Law of Sines)

在一个三角形中，各边和它所对角的正弦的比值相等。

证明：在△ABC中，CD是AB边上的高，则 CD = a · sinB = b · sinA，可得

同理，作其他边上的高又可得

 
用另外一种方法来证明：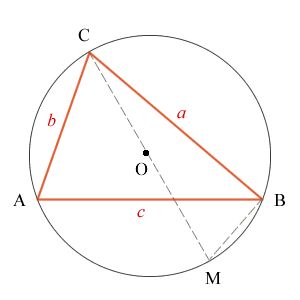
作△ABC的外接圆，圆心为点O. 连接CO并延长交⊙O于点M，连接BM. 可得∠A = ∠M，则 BC = CM · sinM
即 a = 2r · sinM = 2r · sinA
同理可得 b = 2r · sinB, c = 2r · sinC
∴

一般地，把三角形的三个角A，B，C和它们的对边a，b，c叫做三角形的元素。已知三角形的几个元素求其它元素的过程叫做解三角形(Sloving Triangles)。

2.   余弦定理(Law of Cosines)

三角形中任何一边的平方 = 其它两边的平方和减去这两边与它们的夹角的余弦的积的两倍。

a² = b² + c² – 2bc · cosA

b² = a² + c² –2ac · cosB

c² = a² + b² – 2ab · cosC

证明：通过向量的数量积

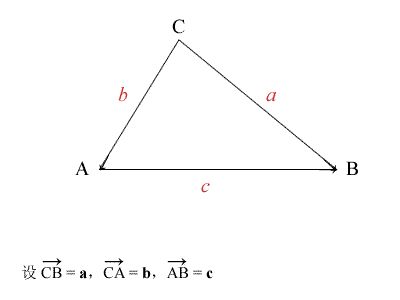
则 c = a – b

| c | ² = (a – b) · (a – b)

= a·a + b·b – 2a·b

= a² + b² – 2ab · cosC

从余弦定理，可以得到

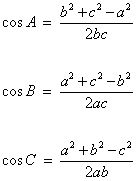
与正弦定理和余弦定理相关的其他公式 

1.  模尔外得公式：此公式可以对计算结果的验证

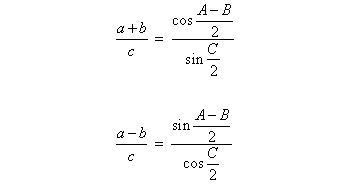
2.  设三角形外接圆的半径是R，则 a = 2R sinA， b = 2R sinB， c = 2R sinC

3.  

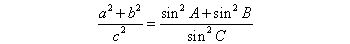
练习：

1. △ABC中, ∠C = 30°, 在下列条件中，△ABC有两解的是( )
( A ) a = 5, b = 2
( B ) b = 2, c = 5
( C ) c = 4, a = 3
( D ) a = 4, c = 3

 
2. 解△ABC，
( 1 ) 已知∠A = 30°, b = 8, a = 3.
( 2 ) 已知∠A = 30°, b = 8, a = 4.
( 3 ) 已知∠A = 30°, b = 8, a = 5.

3. △ABC中, a = b = c + 2, cosA = 3 / 5, 求a、c.

来源 | 玄数，清纯世纪尊重原创，如涉及版权问题，请联系我们删除。

不是我说， 在看的各位都是神仙