三角函数及其之间的关系

正弦函数:sin x

余弦函数:cos x

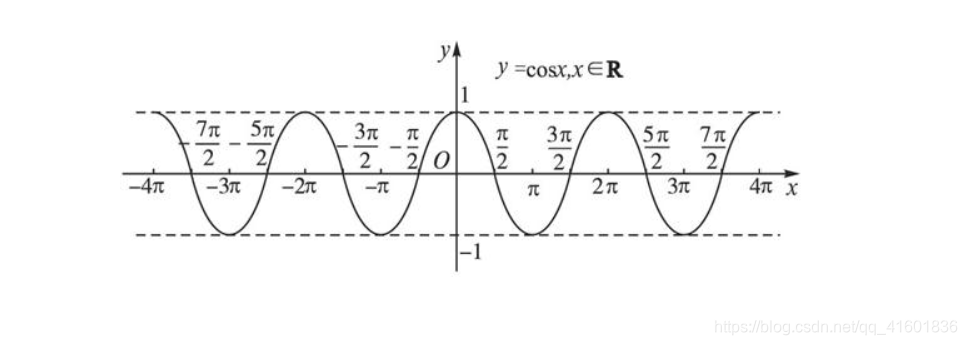
正切函数:tan x

余切函数:cot x

正割函数:sec x       读音:[si:kent]

余割函数:csc x       读音:[keu'si:kent]

 

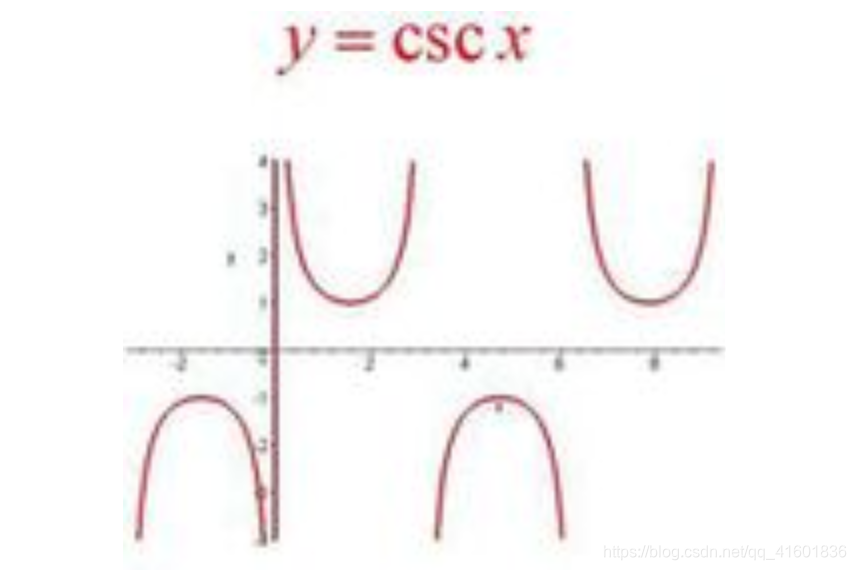
其中

tan x = sin x/cos x

cot x = cos x/sin x

sec x = 1 / cos x

csc x = 1 / sin x

 

 

 

同角三角函数间的基本关系式： 
·平方关系： 
sin^2(α)+cos^2(α)=1 
tan^2(α)+1=sec^2(α) 
cot^2(α)+1=csc^2(α) 
·商的关系： 
tanα=sinα/cosα 

cotα=cosα/sinα 

·倒数关系： 
tanα·cotα=1 
sinα·cscα=1 
cosα·secα=1 
三角函数恒等变形公式： 
·两角和与差的三角函数： 
cos(α+β)=cosα·cosβ-sinα·sinβ 
cos(α-β)=cosα·cosβ+sinα·sinβ 
sin(α±β)=sinα·cosβ±cosα·sinβ 
tan(α+β)=(tanα+tanβ)/(1-tanα·tanβ) 
tan(α-β)=(tanα-tanβ)/(1+tanα·tanβ) 

·倍角公式： 
sin(2α)=2sinα·cosα 
cos(2α)=cos^2(α)-sin^2(α)=2cos^2(α)-1=1-2sin^2(α) 
tan(2α)=2tanα/[1-tan^2(α)] 

·三倍角公式： 
sin3α=3sinα-4sin^3(α) 
cos3α=4cos^3(α)-3cosα 

·半角公式： 
sin^2(α/2)=(1-cosα)/2 
cos^2(α/2)=(1+cosα)/2 
tan^2(α/2)=(1-cosα)/(1+cosα) 
tan(α/2)=sinα/(1+cosα)=(1-cosα)/sinα 

·万能公式： 
sinα=2tan(α/2)/[1+tan^2(α/2)] 
cosα=[1-tan^2(α/2)]/[1+tan^2(α/2)] 
tanα=2tan(α/2)/[1-tan^2(α/2)] 

·积化和差公式： 
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)] 
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)] 
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)] 
sinα·sinβ=-(1/2)[cos(α+β)-cos(α-β)] 

·和差化积公式： 
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2] 
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2] 
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2] 
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]