变换矩阵的意思_线性代数(Gelbert)复对称矩阵

    上文书说到复对称矩阵，不只是转置，而是共轭转置才相等。其实可以统一一下，因为实数的共轭就是自己。这里就需要解释一下为什么需要取其共轭了。

    之前有提到过向量的长度，也就是模长，在元素不都为0的情况下，模长是不应该为0的。但是，如果有复数就不一样了，例如：a = [1 i]^T 向量，如果与自己做点积 aa^T = 1² + i² = 1 - 1 = 0，模长是零这事儿就比较尴尬了。不过，说实在的，这点尴尬对我来说，说服力还是有点不太够，我来补充个我的证明。

    其实要说说服力，应该还是足够的，因为可以举个反例，比如这个对称矩阵：

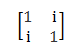
    求它的特征值 λ² - 2λ + 1 - i² = λ² - 2λ + 2 = 0，它的判别式 b² - 4ac < 0，所以它没有实数特征值(说白了，关注的并不是对称矩阵的特征值和特征向量是不是好，而是关注什么矩阵特征值和特征向量好)。观察 b² - 4ac 可以发现这个矩阵如果是三角阵的时候就刚好是实数和虚数特征值的临界线，判别式等于零。那么只要反对角线上的值不出现多出来的正数就有实特征值。

    以二阶对称阵为例，因为三、四阶的太复杂了，五阶以上群论我还没学明白，也不敢乱说，不过形式就是那么个形式，二阶的可以，其他阶至少心理上就能接受了。反正行列式的值就是那么个求法，还有反例，我想也凑合了，要啥自行车(还是有点心虚的，不过以后再说了，上班路上空想也就想到这个程度)。

    下面这三段纯属我路上胡思乱想，完全可以不看，主要是想了这么多，不写上总觉得不开心。

    首先，由于是对称矩阵，共不共轭，对称轴也就是对角线肯定是实数，因为对称轴不能因为翻转就变了。既然对称轴是实数，那么根据中学学的因式分解可知，特征值一定是实数，不知道的参考《特征向量》的求法或者找我讨论。

    提到二阶方程的根，韦达定理是跑不掉的，设a、b、c是二次方程系数，由于是特征向量，a 就可以等于1不考虑了，于是b =  - (λ₁ + λ₂)、c = (λ₁ × λ₂)，b² - 4ac ≥ 0，其中 b 是矩阵的迹的相反数，c 是行列式。接下来，需要把 b 和 c 联系起来，那最简单的就是均值不等式了(对了，三阶不知道会不会用到调和平均数)：几何平均数小于等于算数平均数。这里很明显 b 和 c 异号，先假设两根是正数(其实负数也是一样的，符号换一边而已，不等号总是要变方向的)，有 -b /2 ≥ c 的平方根。当几何平均数取最大值，也就是 λ₁ = λ₂ 时，几何平均数等于代数平均数，不等式两侧平方 b² / 4 = c。也就是说，对称矩阵中只有实数的情况下，最接近虚数的是判别式为零的时候。如果让对称矩阵出现虚特征值，就需要让判别式小于0，而矩阵的对角线很难动手脚，但是行列式可以。只要让行列式非对称轴的元素，对于二阶矩阵就是反对角线上的数，越减越大就好了。反对角线上的两个数相等，如果是实数，无论正负积一定是正数，但是如果包含虚部，再加上反对角线的负号，那么得到的 c 一定会比预期的大，在极端情况中，例如两根相等时，就会出现判别式小于0的情况，就会出现虚根。

    而要避免出现这种情况，复对称矩阵的对角线两边的虚数部分就不能是完全一样的，而是应该共轭。就是说，复对称矩阵不是转置以后与原矩阵一样，而是转置再共轭以后一样。在《对称矩阵》结尾处，我列了的内容中，本来以为Gelbert会忽略过去的一个概念，Hermitian 矩阵就是这个意思，自共轭矩阵，没想到他这节课讲了。共轭转置可以用H简单表示：

Z^H = Z^*T

Z^HZ = |Z|²(模长的平方)

    于是，对于复数向量、矩阵的内积就不是简单的 Z^TZ，而是 Z^HZ了，多了一个共轭的过程。对于对称矩阵，有了埃尔米特矩阵这个概念(H不发音)，然后上一篇结尾处另一个我以为会忽略的概念，Gelbert也在这一课讲了：酉矩阵。如有了复数的对称矩阵对应自共轭矩阵，酉矩阵对应复数的标准正交矩阵，列向量正交，《标准正交矩阵》是酉矩阵只有实数的特例，U^HU = I、U^H = U^-1。U 中的向量 u_i^Hu_j 与 实数时 Q 中的 q_i^Tq_j 一样，当 i = j，是同一个向量，结果为模长平方 1；当 i ≠ j，两向量垂直，结果为零。

    最著名的酉矩阵，语音识别跑不掉的，其实只要和波有关，很振动有关就能拉上关系的，来源于傅里叶变换(离散的，DFT)的矩阵，接下来要讲的(定语超长的)傅里叶矩阵。

    傅里叶矩阵的形式是：

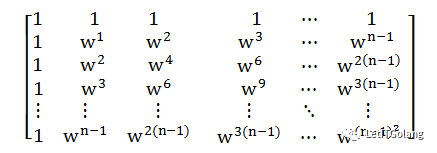
    形式是这个形式，不过有一点问题，因为它不是标准正交矩阵，看第一行和第一列就知道，于是还得乘个n的平方根倒数在前面：

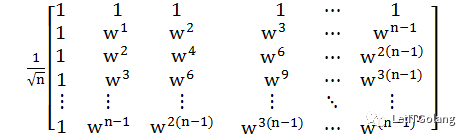
    这个计数方式，作为程序员会比较熟悉，Gelbert也特地提到了，从0开始。从0开始的好处，我觉得是wº = 1，这样可以用行标和列表统一的表示矩阵元素(e) w^i×j = e_ij，i ∈ 0...n-1。

    这里的w是n次单位根，就是说 wⁿ = 1。

   求n次单位根，就涉及到了棣莫弗定理，先从复数的乘法开始。前面看的a+bi形式是复数的代数形式，它还有三角形式，在三角行驶中，复数的模长就相当于极坐标系中的极径，想象一条极径扔到直角坐标系中，实数部分就是它到x轴的投影a = rcosθ，虚数部分就是到y轴的投影b=rsinθ。于是，两个复数的乘法就可以表示为：

(r₁cosθ₁+ir₁sinθ₁)(r₂cosθ₂+ir₂sinθ₂) 

= r₁cosθ₁r₂cosθ₂ + r₁cosθ₁ir₂sinθ₂ 

+ ir₁sinθ₁ir₂sinθ₂ + ir₁sinθ₁r₂cosθ₂

= r₁r₂cosθ₁cosθ₂ - r₁r₂sinθ₁sinθ₂

+ ir₁r₂cosθ₁sinθ₂ + ir₁r₂sinθ₁cosθ₂ 

    由于：

cos(θ₁+θ₂) = cosθ₁cosθ₂ - sinθ₁sinθ₂

sin(θ₁+θ₂) = sinθ₁cosθ₂ + cosθ₁sinθ₂

r₁r₂cosθ₁cosθ₂ - r₁r₂sinθ₁sinθ₂

+ ir₁r₂cosθ₁sinθ₂ + ir₁r₂sinθ₁cosθ₂

= r₁r₂cos(θ₁+θ₂) + ir₁r₂sin(θ₁+θ₂)

    也就是模长相乘，幅角相加。求单元根 (rcosθ+irsinθ) ⁿ = 1 ，就相当于上式中由第一个 rcosθ+irsinθ 开始累乘 rcosθ+irsinθ，由于模长 rⁿ = 1，θ角每次累加一个θ:

(rcosθ+irsinθ) ⁿ = rⁿ[cos(nθ) + isin(nθ)]

=cos(nθ) + isin(nθ) = 1

    由于cos(nθ) + isin(nθ)  = 1 = 1 + 0i，所以cos(nθ) = 1，于是 nθ 角的斜边一定在x轴的正半轴上，sin(nθ) = 0的 nθ 可以有两种取值，但是符合cos 的只有 0°。由于是周期2π的周期函数，nθ一定是2π的整数倍，设k是整数，于是：θ = 2kπ / n。Gelbert没有用2kπ，直接用的2π，因为反正也相等吧，或者简单之类的原因。

    结合《幂级数和欧拉公式》中提到过的欧拉公式，可得：

cos(nθ) + isin(nθ) = e^(2π/n)i = 1 

    这里只有n是变量，于是单元根就有n个取值，它们将2π等分成了n份，其中的第一个，在x正半轴上的是原根。

    说了这么多，终于可以开始稍微介绍一下正主了：快速傅里叶变换( Fast Fourier Transform, FFT )。这东西应用广泛，比如我最近在搞的 Kaldi 中，提取音频特征，计算功率谱就用了，其它还有很多地方。它借助傅里叶矩阵可以将 n×n 阶的矩阵乘法运算从 O(n²) 优化到 O(nlog₂n)，在大规模运算中有作用巨大。

    然而，我想了好久怎么写这一块，Gelbert只是简单的介绍了下如何用，总结一下就是：

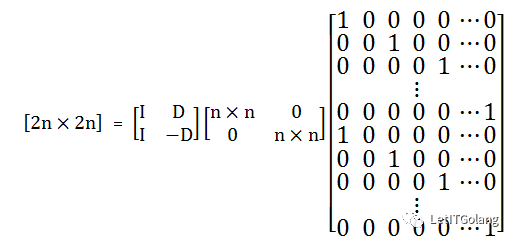
    其中：

    做这个分解是因为2n×2n的矩阵参与运算的计算量太大，而分解之后计算量小了很多。本来一个边就是2n个元素，但是分解之后矩阵稀疏了，相对需要乘的元素少了，有些计算分块以后变成了加法，原来需要做4n²次运算较少为2n²+n次。并且n还可以继续分为n/2直到1，由于每次规模减半，那么其中一个2n就简化为了以2为底的对数，常系数什么的，大O渐进意义下忽略就好了。

    本来作为一个程序员，我对逻辑更感兴趣，推导证明数学公式还挺开心的，套公式复述一遍就实在提不起兴趣了。不过，这个要推导就太长了，简单来说，离散傅里叶变换在信号比较弱的时候算法复杂度很高，为了解决这个问题，通过数学推导，将 类似(e^(2π/n)i)² = e^(π/n)i、 (e^(2π/n)i)ⁿ = -1等指数和e的性质带入公式，进行一些指数的二项式分解、化简、代换，然后通过对0、1分别讨论奇偶信号的离散傅里叶变换，这里的计算奇偶序列会重新排序，这可能就是上面公式里的奇偶置换矩阵。这都是复变函数、信号系统等科目的内容。

    要是想细细的讲明白可能得从傅里叶级数开始(可不是我写的傅里叶级数那么简单的内容，从分段可导函数开始、狄利克雷积分什么的)，如果我哪天突然劲头上来了的话，倒是也说不定，可能就写一个系列。不过这就和这课没啥关系，感觉严格来说都不像是一类内容(我这一系列里写的傅里叶级数感觉也不像)。

---

公众号：