从像素坐标到相机坐标_多视图几何基础——深入理解相机内外参数

上一篇：前言（comming soon）

关键词：相机模型，多视图几何，相机内参数，相机外参数，skew畸变

1. 针孔相机模型

Figure 1

针孔相机模型是一种理想化的简单相机模型，也是成像的最基本原理，在这种模型中，有一个暗室，暗室中有一个足够小的针孔，外部世界的光线通过这个针孔进入暗室盒子，光线投射到暗室盒子中的二维平面，即将一个三维的场景（Scene）映射成了一张二维的影像。

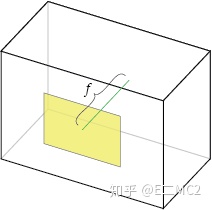
这个针孔到成像平面的距离，叫做焦距（focal length）f：

Figure 2

由于在上述过程中像平面中的图像和实际场景中的影像是镜像的。为了让成像的过程更加直观，我们假象一个平面，这个平面位于相机针孔前距离针孔f的距离，在这个平面上场景的成像没有被镜像，拥有和真实场景相同的方向，我们把这个假象的平面称为像平面（image plane），这个假想的平面上的成像避免了数学计算时的正负号反转，如Figure 3所示

Figure 3

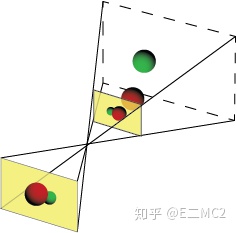
然而，通过理论上的这个无穷小的针孔进入的光线是极其有限的，我们可以通过扩大这个“针孔”来增加进光量，但是三维世界中的不同的位置通过这样的较大的一个孔会投射到成像平面上的同一个位置造成模糊的成像。解决这个问题的一种办法是采用一个透镜在聚焦通过这个较大的孔的光线，然而即使最优秀的透镜也只能保证在三维世界中一定的距离范围的光源投射到成像平面清晰，这个成像清晰的范围被称为景深（depth of field），在这个景深范围内的三维物体的成像几何接近于上述的针孔相机模型，这里提到的“针孔”我们将其称为投影中心（center of projection）或相机中心(camera center)。这个理想的模型的投影过程，我们将其称为透视投影（perspective projection）。顺便提及一点，为了减小成像形变使成像的几何更加的接近针孔相机模型，现实中这里所述的透镜通常是一系复杂的透镜的组合，而不是一个简单的凸透镜。

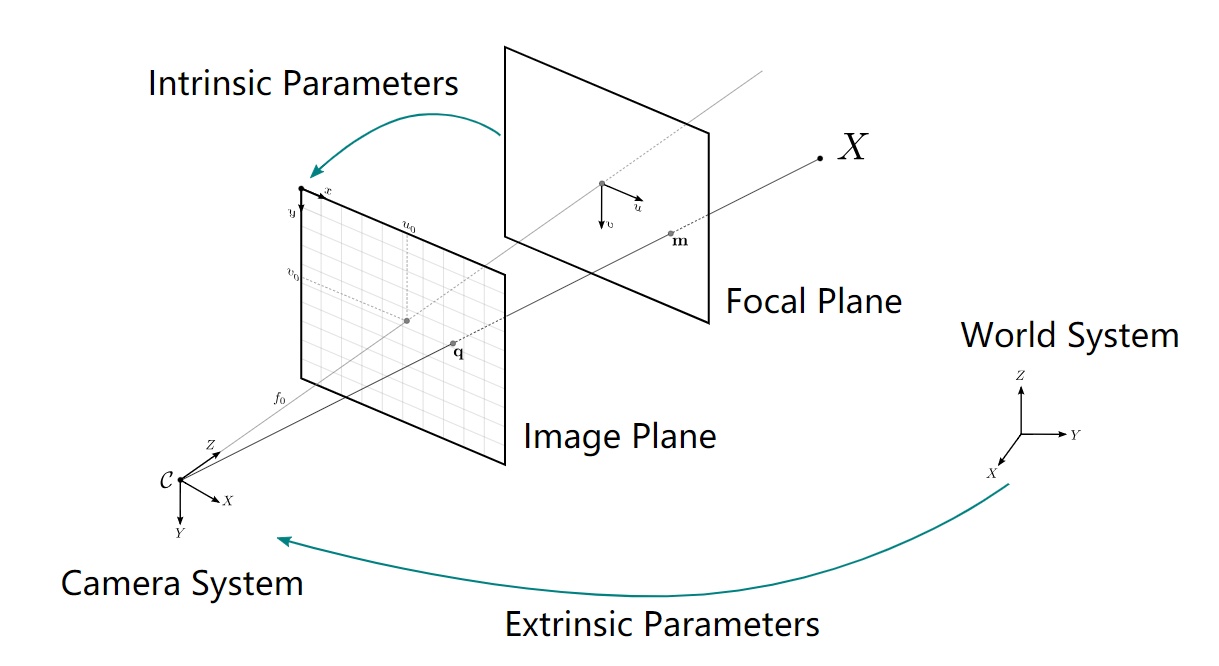
2. 以相机坐标系为参考的针孔相机的成像几何

Figure 4

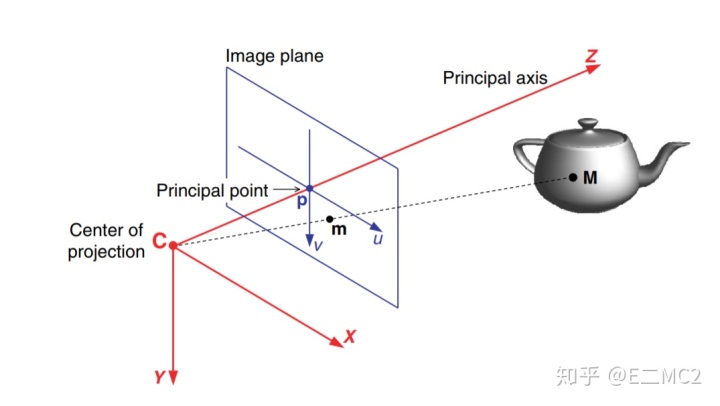
为了将三维世界的场景映射到二维影像的过程建立数学模型，我们先考虑将相机自身的坐标系作为参考来建立投影过程的数学关系，如Figure 4所示为一个以相机为中心的坐标系（camera-centered reference frame）,这是一个右手坐标系，其坐标原点为之前所述的投影中心。它的Z轴为相机的主光轴——通过投影中心并且垂直于像平面的直线，在这样的坐标定义下，像平面的表达式为

，其中f为相机的焦距，主光轴与像平面的交点被称为像主点（principal point）。在相机坐标系中还包括一个互相正交的像平面坐标系

，三维空间中的一个点M在像平面坐标系上的成像为m，即通过投影中心与三维点M的直线与像平面的交点。若点M在相机坐标系中的坐标为

，则位于直线

上的任意一点的坐标为

,其中

为一实数，直线与像平面的交点必须满足公式

,可得

，进而有点M的像m的坐标为

，其中，

。 （1-1）

在上述过程中，我们所采用的像平面坐标都是基于公制单位（metric unit）的（即以米为单位），坐标

都是可以无限细分的长度，然而，现实中我们无法用无限的精度来表示像平面上的坐标，在影像数字化的过程中，传感器由一个栅格化的物理单元组成，构成感光元件的最小单元称为图像元素（picture elements），简称像素（pixels）。这些像素通常规整的在成像平面上排布成规则矩形，如图Figure 5所示。

Figure 5

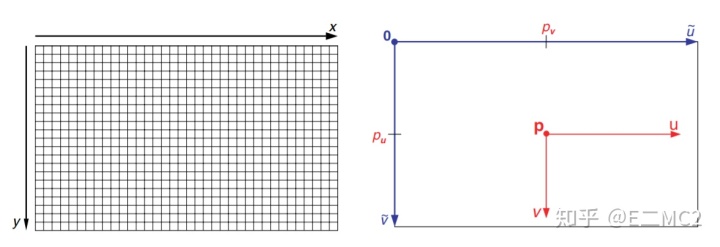
在计算机视觉的大多数约定中，像素的位置可以通过像素在像平面上所处的行列来索引，并且将影像的左上角规定为坐标系的原点，这里所说的用来索引像素位置的行列的数字被称为图像的像素坐标（pixel coordinates），我们将其表示为

，其中， 规定

沿水平方向，向右为正，

沿竖直方向，向下为正。这样的坐标定义有以下优点：

1. 像素被赋予的
   坐标数值递增的顺序与数码相机内部的传感器的像素的读取(read out）顺序一致：从图像的左上角开始，逐行的读取；
2. 相机坐标系通常采用的右手坐标系，这样的坐标规定意味着相机坐标系的Z轴由相机的位置指所摄三维场景，在这样的坐标定义下，场景中的点的Z坐标即为该点相对于相机的深度（depth），这个深度即是三维重建中很多过程中试图求解的未知数；

由于我们无法用无限的精度来表示像平面上的坐标，我们在影像处理及三维重建的过程中并不关心某一像点的公制坐标

,而是更多的关注其像素坐标

，这个坐标是我们可以直接从一张影像上获取的，而公示（1-1）中得到的像平面坐标是公制的，下面我们将介绍两者之间是如何转换的。

在上述两种定义在像平面的坐标系中，坐标轴

和坐标轴

的方向定义是一致的，但像素坐标的原点的定义是影像左上角，而公制的像平面坐标的原点定义为像主点，在进行这两个坐标系的转换之前我们首先将其坐标的定义统一到影像的左上角，我们将像平面坐标的定义进行一个平移，我们将像主点的

相对于图像左上角的公制单位表示为

，分别表示像主点相对于图像左上角在水平方向和竖直方向的公制距离，于是平移原点后的公制像平面坐标变为：

接下来要将上述公制的坐标转换为像素坐标值需要将其除以一个像素的公制的长宽，我们用

分别表示一个像素的长宽的倒数，于是有：

等价的，

（2-1）

其中，

是焦距在

两个方向上以像素为单位的焦距，

为以图像左上角为原点的像素坐标系下像主点的坐标，比例

表示像素的比例，称为像素纵横比（aspect ratio）。顺便一提，在opencv中的相机内参

均是指以像素为单位的分别与这里的

对应。在一个理想的针孔相机模型中，像素为单位的焦距

具有相同的值：

然而在现实中，由于以下一些原因数值上会有一些不同：

1. 相机传感器的制造缺陷；
2. 影像在后期处理中经过了非等比缩放；
3. 相机镜头引入了非预期的畸变；
4. 相机采用了某种带有长宽比变形的格式，在这种格式中镜头将一个宽场景压缩到了标准的画幅；
5. 相机标定中产生的误差；

以上各个因素均导致最终的像素变形为非标准正方形。

采用来个不同方向的焦距值来表示相机的焦距并不是很直观，因为他无法与一个物理的焦距的概念对应起来（物理焦距只有一个，无法分为水平和竖直两个方向），一些教科书中采用一个焦距值

和一个描述非标准正方形像素变形的纵横比

来表示两个焦距，这样更方便的将非正方形像素表达为一中形变，避免产生两个焦距的概念。

3. 相机坐标系下投影的矩阵表达

如果我么借助齐次坐标系，我们可以将上述公式（2-1）更加优雅的表达为矩阵的形式，齐次坐标系可以简单的理解为在原始的坐标下添加一个维度并将其值为数值1，同时我们将其坐标采用列向量来表示，这样原来像点m的坐标

可以表示为

，则其矩阵的表达如下：

通过上述矩阵可以得到，如果我们将像点的齐次坐标

认为是三维空间中的一条直线，

即为三维点

在相机坐标系下的深度，上述的3X3的矩阵

表示了从一个三维世界中的物理量测单位（m，cm或mm）是如何映射到以像素为单位的数字影像上的。这个矩阵被称为相机矩阵（calibration matrix），也称为相机内参矩阵（camera instrinsic），其更加通用的表达是一个上三角矩阵：

其中的参数

被称为

，这个参数用来建模像素是平行四边形而不是矩形，这个参数同样可以认为是传感器的安置不严格与相机主光轴垂直造成的变形的近似，事实上

与像素坐标系的X，Y轴之间的夹角

的正切值

成反比，因此当

时，表示像素为矩形。

为更加直观的理解相机内参矩阵可以将其拆分为几个连续的2D变换：

同样，为了更加直观的理解

对成像的影像，以下图为例进行说明：

为零的成像示意图及所成影像如下：

Figure 6

不为零的成像示意图及所成影像如下：

Figure 7

有了上述基础，我们可以更加简单的矩阵形式将投影关系表示为：

其中

是三维空间中的点M在相机坐标系中的坐标，

是一个正实数，表示了某一个点在相机坐标系下的深度，由于矩阵

的最后一行为

有

,因此

被称为对应于像点m的物方点M的投影深度（projective depth）。

4. 基于任意坐标系为参考的成像几何

当我们的场景中有多余一个相机或者我们的场景需要表示在某一指定的全局唯一的世界坐标系（world frame）下时，相机的位置和姿态将有一个相机中心

和一个旋转矩阵

表示相机坐标系相对于世界坐标系的平移和旋转，旋转矩阵

中的每一列

是相机坐标系的坐标轴在世界坐标系中的方向向量，如Figure 8所示，相机中心

和相机旋转矩阵

唯一确定了相机坐标系在世界坐标系中的位置姿态，我们将其称为相机外参（external parameters）。

Figure 8

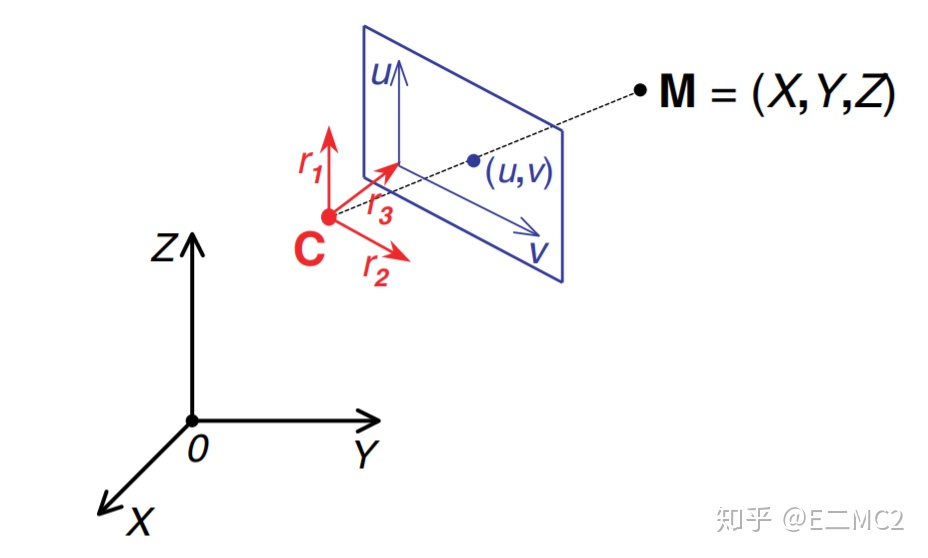
世界坐标系中的一个三维点M要转换到相机坐标系下去，我们只需要将表示两个坐标系之间的相对平移的向量

正交地投影到世界坐标系下表示相机坐标轴的三个方向向量

上，即向向量

分别与相机坐标轴的三个方向

点乘（向量的内积），等价的以矩阵的形式可以表示为

，于是之前所述的投影映射关系变为：

其中，

为世界坐标系下的三维点的坐标列向量，

为像素坐标系下的其次坐标的列向量，

分别表示相机坐标系相对于世界坐标的平移和旋转。

一些教科书中也会将场景中的点M也采用齐次坐标来表示，即

,可得映射关系如下：

令

，矩阵

是一个3X4的矩阵，由于其包含了一个物方三维点映射到像素坐标系下的相机内外参数，矩阵

被称为相机的投影矩阵（projection matrix），顺便一提，如果矩阵

是已知的，我们可以从其中分解出相机的内外参数：投影矩阵的前三行三列由

构成，其逆为

，其中旋转矩阵

为正交矩阵，矩阵

为非奇异的上三角矩阵，根据线性代数的知识：任意的3X3的矩阵都有可以通过QR分解，唯一的分解为一个正交矩阵和一个非奇异的上三角矩阵的积，我们就可以分别求出矩阵

,进而结合投影矩阵的第四列求出相机中心

，这里在分解前先将

求逆是因为QR分解是唯一的，而RQ分解不唯一。与相机内参矩阵及旋转矩阵对矩阵有诸多的限制不同的是，任意的一个3X4的矩阵，只要其前三行三列的矩阵为非奇异矩阵他就可以被视为一个投影矩阵。

5. 非线性畸变

截至目前为止，上述所讨论的所有成像几何中都认为相机中心

，场景中的三维点

，及

在像平面的成像

三点共线，这三点处于同一条直线的几何关系在摄影测量中采用共线方程来描述，可以说这是多视图几何的基础。然而在现实中由于相机需要镜头来汇聚光线，镜头使得成像的过程并不完美的遵从这个理想的共线关系，我们以径向畸变为例，讨论加入镜头畸变因素后的映射关系，我们将为考虑畸变的像平面坐标加上下标_u加以区分：

像点

到像主点的距离为：

于是考虑畸变的像平面坐标变为：

最总终的像素坐标为：

我们这里将相机的畸变置于相机的外参数与内参数之间，也可以将畸变参数应用在像素坐标系的坐标之上。实际中相机畸变的建模通常还会有非径向的非对称的切向畸变，Brown-Conrady镜头畸变模型是一种常用的畸变模型，关于相机畸变更多的内容可以参考Distortion。如果镜头的畸变参数已知我们可以计算出影像上各个像素畸变前的位置，这个过程叫做畸变矫正(undistort)，畸变校矫正后的影像可以近似的认为其满足相机中心、三维空间中的点极其成像三点共线。后续我们的介绍中均认为影像已经经过了畸变矫正。

下一篇: 三维重建（comming soon）