怎么判断要用左右极限_函数左、右极限简介

分三个小节简单介绍一下左、右极限。

一、极限与左、右极限的联系

二、如何求左、右极限

三、左、右极限的常见应用

一、极限与左、右极限的联系

比较这三个定义我们会发现：

也就是说我们平时所求的极限，其实本质上都是先求了左、右极限，然后二者相等，才得到了我们的函数极限。

即：

二、如何求左、右极限

但实际上，我们发现我们很少这样做。很少先求左右极限，然后再比较得到极限。

这是因为我们数学分析研究的基本上都是连续函数，而连续函数在定义域内，左右极限（非区间端点处）都是存在且相等的，且等于这一点的函数值。

上面这句话，就意味着我们求连续函数在一点左极限、右极限、极限时，就是求得这一点的函数值。

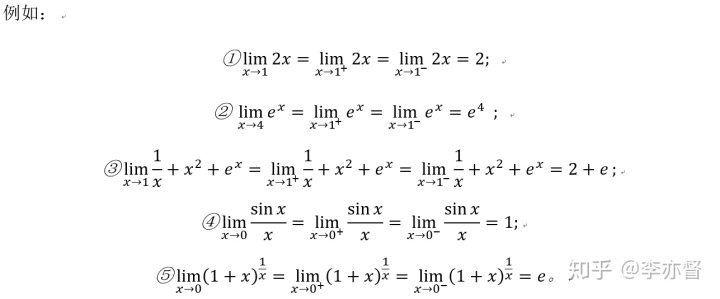
所以我们在求连续函数的左右极限时，就是把这点带入即可。

三、左、右极限的常见应用

我们考查左右极限的题目，挑选的都是一些有可能左右极限不同的（含有不连续点）函数：如分段函数、含绝对值的函数、自变量趋于无穷的指数函数…

（一）判断这些特殊函数的极限是否存在

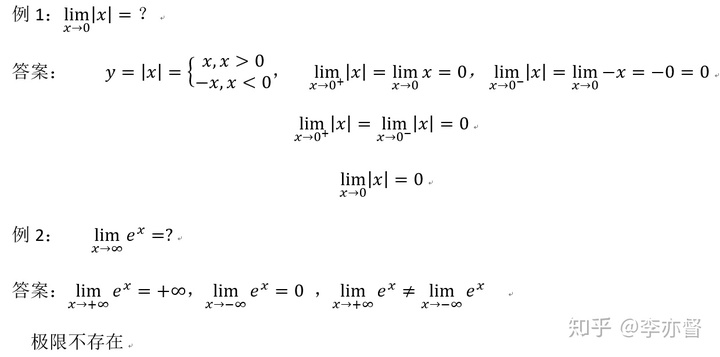
（二）判断函数在某点的连续性

根据定义判断连续性时，需要用到左右极限。

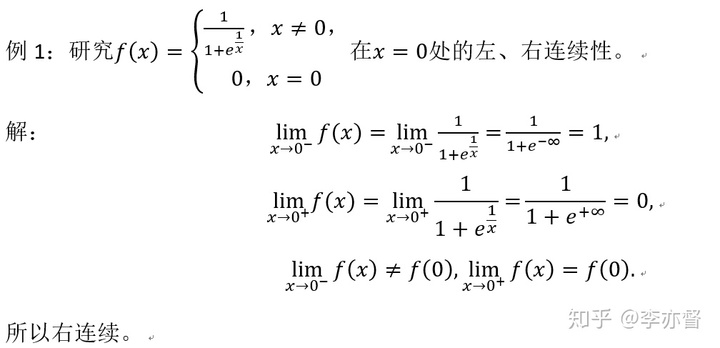
后续再据情况补充。