梯度下降算法_用人话讲明白梯度下降Gradient Descent

文章目录

1.梯度

2.多元线性回归参数求解

3.梯度下降

4.梯度下降法求解多元线性回归

梯度下降算法在机器学习中出现频率特别高，是非常常用的优化算法。

本文借多元线性回归，用人话解释清楚梯度下降的原理和步骤。

1.梯度

梯度是什么呢？

我们还是从最简单的情况说起，对于一元函数来讲，梯度就是函数的导数。

而对于多元函数而言，梯度是一个向量，也就是说，把求得的偏导数以向量的形式写出来，就是梯度。

例如，我们在用人话讲明白线性回归LinearRegression一文中，求未知参数β0 和β1 时，对损失函数求偏导，此时的梯度向量为：

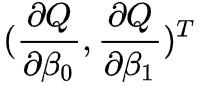
其中：

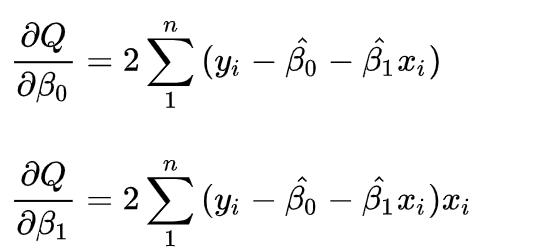
那篇文章中，因为一元线性回归中只有2个参数，因此令两个偏导数为0，能很容易求得β0 和β1 的解。

但是，这种求导的方法在多元回归的参数求解中就不太实用了，为什么呢？

2.多元线性回归参数求解

多元线性回归方程的一般形式为：

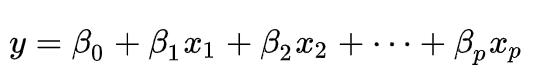
可以简写为矩阵形式(一般加粗表示矩阵或向量)：

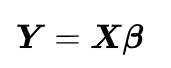
其中，

之前我们介绍过一元线性回归的损失函数可以用残差平方和：

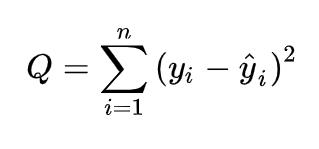
代入多元线性回归方程就是：

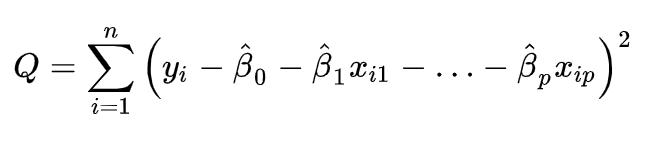
用矩阵形式表示：

上面的展开过程涉及矩阵转置，这里简单提一下矩阵转置相关运算，以免之前学过但是现在忘了：

好了，按照一元线性回归求解析解的思路，现在我们要对Q求导并令导数为0(原谅我懒，后面写公式就不对向量或矩阵加粗了，大家能理解就行)：

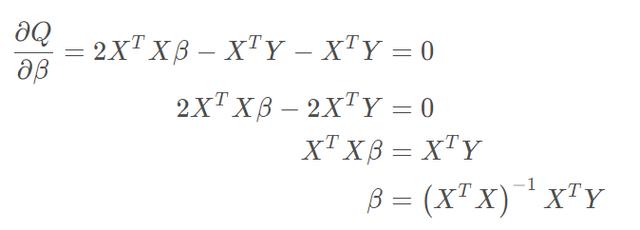
上面的推导过程涉及矩阵求导，这里展开讲下，为什么

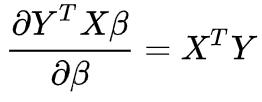
其他几项留给大家举一反三。

首先：

为了直观点，我们将YTX 记为A，因为Y是n维列向量，X是n×(p+1)的矩阵，因此YTX是(p+1)维行向量：

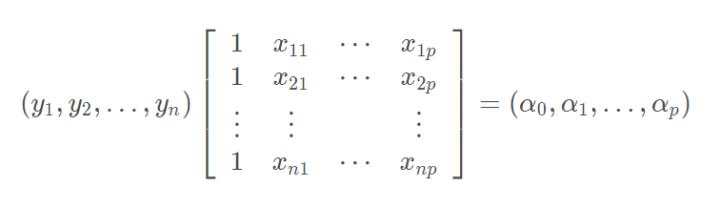
那么上面求导可以简写为：

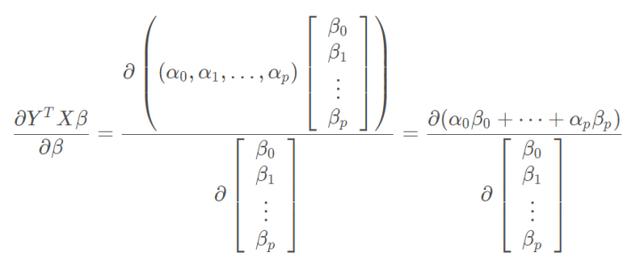
这种形式的矩阵求导属于分母布局，即分子为行向量或者分母为列向量(这里属于后者)。

搞不清楚的可以看看这篇：矩阵求导实例，这里我直接写出标量/列向量求导的公式，如下(y表示标量，X表示列向量)：

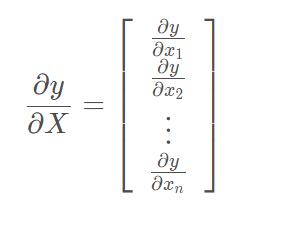
根据上式，显然有：

前面我们将YTX记为A，那么上面算出来的结果就是AT ，即

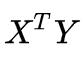
说了这么多有的没的，最终我想说是的

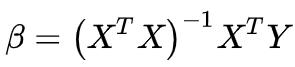
里面涉及到矩阵求逆，但实际问题中可能X没有逆矩阵，这时计算的结果就不够精确。

第二个问题就是，如果维度多、样本多，即便有逆矩阵，计算机求解的速度也会很慢。

所以，基于上面这两点，一般情况下我们不会用解析解求解法求多元线性回归参数，而是采用梯度下降法，它的计算代价相对更低。

3.梯度下降

好了，重点来了，本文真正要讲的东西终于登场了。

梯度下降，就是通过一步步迭代，让所有偏导函数都下降到最低。如果觉得不好理解，我们就还是以最简单的一元函数为例开始讲。

下图是我用Excel简单画的二次函数图像(看起来有点歪，原谅我懒……懒得调整了……)，函数为

y=x^2 ，它的导数为y=2x。

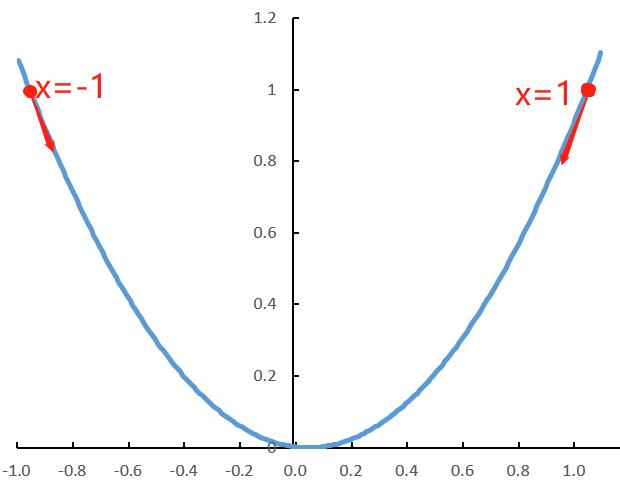
如果我们初始化的点在x=1处，它的导函数值，也就是梯度值是2，为正，那就让它往左移一点，继续计算它的梯度值，若为正，就继续往左移。

如果我们初始化的点在x=-1处，该处的梯度值是-2，为负，那就让它往右移。

多元函数的逻辑也一样，先初始化一个点，也就是随便选择一个位置，计算它的梯度，然后往梯度相反的方向，每次移动一点点，直到达到停止条件。

这个停止条件，可以是足够大的迭代步数，也可以是一个比较小的阈值，当两次迭代之间的差值小于该阈值时，认为梯度已经下降到最低点附近了。

二元函数的梯度下降示例如上图(图片来自梯度下降)，对于这种非凸函数，可能会出现这种情况：初始化的点不同，最后的结果也不同，也就是陷入局部最小值。

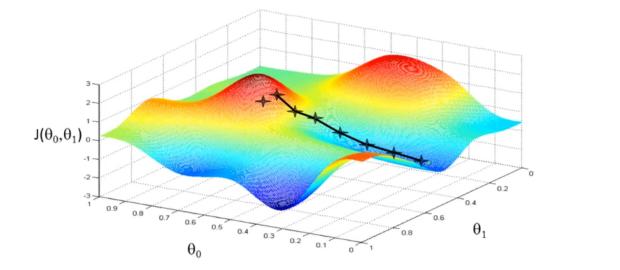
这种问题比较有效的解决方法，就是多取几个初始点。不过对于我们接下来讲的多元线性回归，以及后面要讲的逻辑回归，都不存在这个问题，因为他们的损失函数都是凸函数，有全局最小值。

用数学公式来描述梯度下降的步骤，就是：

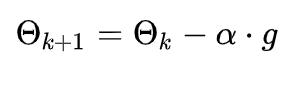
解释下公式含义：

• θk 为k时刻的点坐标，θk+1 为下一刻要移动到的点的坐标，例如 θ0就代表初始化的点坐标， θ1就代表第一步到移动到的位置；
• g代表梯度，前面有个负号，就代表梯度下降，即朝着梯度相反的反向移动；
• α 被称为步长，用它乘以梯度值来控制每次移动的距离，这个值的设定也是一门学问，设定的过小，迭代的次数就会过多，设定的过大，容易一步跨太远，直接跳过了最小值。

4.梯度下降法求解多元线性回归

回到前面的多元线性回归，我们用梯度下降算法求损失函数的最小值。

首先，求梯度，也就是前面我们已经给出的求偏导的公式：

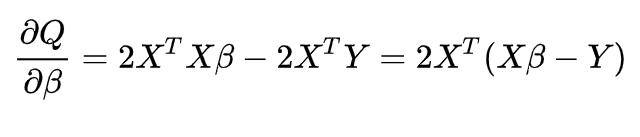
将梯度代入随机梯度下降公式：

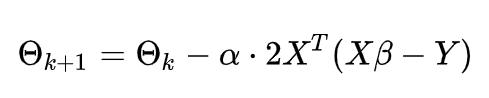
这个式子中，X矩阵和Y向量都是已知的，步长是人为设定的一个值，只有参数β是未知的，而每一步的

θ 是由β 决定的，也就是每一步的点坐标。

算法过程：

1. 初始化β 向量的值，即θ0 ，将其代入导函数得到当前位置的梯度；

2. 用步长α 乘以当前梯度，得到从当前位置下降的距离；

3. 更新θ1，其更新表达式为

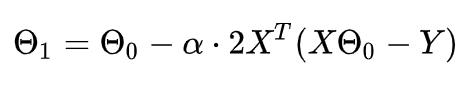
4. 重复以上步骤，直到更新到某个θk，达到停止条件，这个θk就是我们求解的参数向量。

参考链接：

深入浅出--梯度下降法及其实现

梯度下降与随机梯度下降概念及推导过程