机器学习算法（二）：因子分解机FM算法（Factorization Machine）

目录

1 背景

2 poly2算法

3 FM

3.1 FM原理

3.2 FM求解

3.3 度为 2 的因子分解机（FM）模型

3.4 FM 模型交叉项参数的求解详细推导

3.5 用随机梯度法对 FM 模型参数求解

4 时间复杂度 

5 代码

---

1 背景

        Steffen Rendle于2010年提出Factorization Machines（下面简称FM），并发布开源工具libFM。FM的提出主要对比对象是SVM，与SVM相比，有如下几个优势 
（1）对于输入数据是非常稀疏（比如自动推荐系统），FM可以，而SVM会效果很差，因为训出的SVM模型会面临较高的bias。 
（2）FMs拥有线性的复杂度, 可以通过 primal 来优化而不依赖于像SVM的支持向量机。

        因子分解机(Factorization Machine, FM)是由Steffen Rendle提出的一种基于矩阵分解的机器学习算法。目前，被广泛的应用于广告预估模型中，相比LR而言，效果强了不少。是一种不错的CTR预估模型，也是我们现在在使用的广告点击率预估模型，比起著名的Logistic Regression, FM能够把握一些组合的高阶特征，因此拥有更强的表现力。

2 poly2算法

       在做点击率预估时，我们的特征往往来自于用户(user)、广告(item)和上下文环境(context)，在线性模型中，这些特征不进行组合的话，就会发生一个很尴尬的情况，因为：

        所以，对所有用户--我们将得到相同的排序。

        因此我们需要引入一些组合特征作为输入模型，然而仅二阶特征组合的可能性就是原始特征的平方之多，但是由于很多特征其实是相互独立的，他们的组合并没有什么价值。

        LR模型在推荐系统中具有不能对特征进行组合、表达能力不足的问题，ploy2针对这个问题进行了改进，将LR公式的线性部分  改为：

         

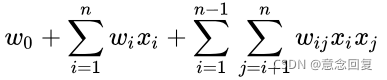
        从上述公式可以看出，ploy2在线性部分增加了二阶特征组合项， 表示组合特征  的权重。对特征进行了两两交叉组合，增加了模型的非线性，提升了模型的表达力。但也不可忽视ploy2的弊端：

        1、特征组合容易引起维度灾难，参数数量从n级别提升至  ，导致模型训练效率极低，甚至可能内存溢出，并且组合的特征大部分并没有效果。

        2、组合特征的样本非常稀疏（样本中找不到某些特征组合），组合特征的权重得不到有效得训练。

        3、增加样本特征而不增加样本数量，易导致模型过拟合。

3 FM

3.1 FM原理

        FM就是一种能够自动把握一些高阶特征的点击率预估模型，可以自动帮助使用者选择合适的高阶输入。

        我们先写出带有所有二阶组合特征的目标函数，其中矩阵W中有n^2个参数，求解非常复杂：

        

        这里每两个特征有一个参数w要学习。

        这里仍有问题：

（1）对于二项式回归来说，如果有n个特征，那么要学习到两两之间的关系，有n(n−1)/2个参数要去学习，对于实际中的复杂任务来说，n的值往往特别大，会造成要学习的参数特别多的问题。 

（2）同时，又由于实际数据会有稀疏性问题，有些特征两两同时不为0的情况很少，当一个数据中任何一个特征值为0的时候，那么其他特征与此特征的相互关系将没有办法学习。

        受到矩阵分解的启发，为了解决上述两个问题，引入了因子分解机。

        如果训练的输入数据有n个特征，设 i, j 两个特征的相互关系用参数 wi,j 表示，那么有wi,j=wj,i这样所有w的参数值会形成一个对称的矩阵，

none     w1,2     w1,3     w1,4   … w1,n 
w2,1    none       w2,3    w2,4    … w2,n

……
wn,1      wn,2      wn,3     wn,4   …  none

3.2 FM求解

        缺失了对角线的矩阵，正因为如此，我们可以通过给对角线任意设定值来保证矩阵为半正定矩阵，自然想到了矩阵分解。

        基于矩阵分解的思想，将以上矩阵分解为两个低阶矩阵的乘积，那么在分解过程中，不仅仅减少了数据存储的复杂度，而且多了一个特别神奇的功能，预测功能。

        矩阵分解基于一个假设，即矩阵中的值等于学习到的两个隐向量的乘积，认为每个特征分量 xi 都可以用一个K维的特征向量vi表示，那么所有特征之前的相关性就也就可以用两个矩阵的相乘进行表示了。

        从上面的式子可以很容易看出，组合部分的特征相关参数共有个。但是如第二部分所分析，在数据很稀疏的情况下，满足都不为0的情况非常少，这样将导致无法通过训练得出。

       为了求出，我们对每一个特征分量引入辅助向量。然后，利用 对进行求解。

 

        那么组成的矩阵可以表示为:

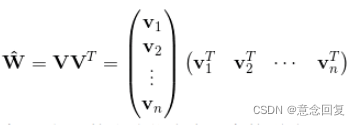
         上面的表达形式，就对应了一种矩阵的分解。对 k 值的限定，就反应了FM模型的表达能力。

3.3 度为 2 的因子分解机（FM）模型

        2-way FM(degree = 2)是FM中具有代表性，且比较简单的一种。 因子分解机的形式为： 

        其中：w_0 为R，W为R^n，v属于R^(n,k);

也就是：

        k是定义factorization维度的超参数，是正整数 。

         <Vi,Vj>表示的是 2 个大小为 k 的向量 Vi 和向量 Vj 的点积：

        

        上式中：Vi 表示的是系数矩阵 V 的第 i 维的向量，且Vi为： 

        

         k 为超参数，且 k 的大小称为 FM 算法模型的度，在因子分解机 FM 模型中，前两部分就是传统的线性模型，最后的那部分将两个互异的特征向量之间的相互关系考虑进去。

        通常，由于数据稀疏，本来wi,j是学习不到的，但是我们可以通过i特征与其他特征的数据，j特征与其他特征的数据，分别学习到i,j特征的参数向量vi,vj，这样b通过vivj的乘积便可以预测wi,j的值，神奇地解决了数据稀疏带来的问题。

        而且，一般隐向量维度k远远小于特征数量n，那么分解后要学习的参数数量为：n∗k,对比多项式回归的参数数量n(n−1)/2, 从O(n^2)减到了kO(n)的级别。

        因子分解机FM也可以推广到高阶的形式，即将更多互异特征分量之间的相互关系考虑进来。

3.4 FM 模型交叉项参数的求解详细推导

        对于交叉项的求解可以效仿如下：

3.5 用随机梯度法对 FM 模型参数求解

        假设数据集 X 中有 m 个训练样本，即

        

         同时每个样本对应一个特征X^(i)：

       

         对于度 k=2 的因子分解机 FM 模型来说，其主要的参数就一次项和常数项的参数 w0,w1....,wn 以及交叉系数矩阵 V ，在利用随机梯度对模型的参数进行学习的过程中，主要是对损失函数 loss 的求导。

  

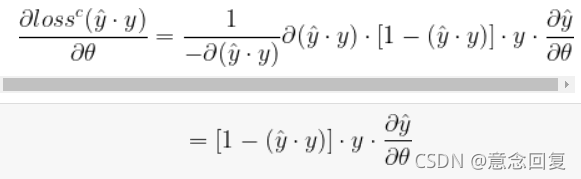
因此：

             

 

4 时间复杂度 

        未引入因子分解机之前的时间复杂度为O(kn^2)。引入因子分解机后，本来需要训练的 n×n 个参数，现在只需要训练 n×k 个，其中 k≪n，时间复杂度就降为 O(kn)。

时间复杂度就降为O(kn)。

5 代码

FM在特征组合中的应用 - 张朝阳 - 博客园

机器学习算法（3）——FM(Factorization Machine)算法（推导与实现）：机器学习算法（3）——FM(Factorization Machine)算法（推导与实现）_ChaucerG的博客-CSDN博客_机器学习fm

FM算法详解：FM算法详解_bitcarmanlee的博客-CSDN博客_fm算法