多元函数的向量表示_机器学习中微积分如何将链式规则应用于多元空间

在机器学习微积分之前的文章中，我们讨论了区分单变量和多元函数的问题。另外，我们开发了演算工具箱来帮助我们导航高维空间。我们特别谈到了连锁规则。在用于机器学习的微积分第4部分中，我们将通过示例研究如何将此链式规则应用于多元空间。

多元链式规则：

之前我们讨论了导数。也就是说，当我们有一个多元函数时，假设f(x，y，z)和变量x，y，z本身是另一个变量t的函数，

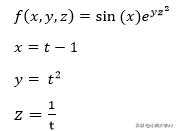
然后使用以下表达式查找f关于t的导数，

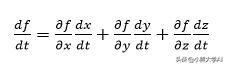
实际上，这是通过三个变量中的每一个将f关联到t的链的总和。

这有助于我们以分段方式而不是替代方式进行解决。我们的计算机可以快速执行分段操作。

我们将以稍微简化的概括这个概念来开始用于机器学习的微积分第4部分。

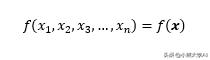
x表示它代表一系列变量，就像n维向量一样。

现在，这些x变量又是某个变量t的函数。我们对找到f关于t的导数感兴趣。

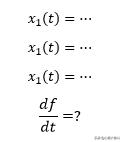
我们将尝试通过每个变量的链之和将f连接到t。

f关于x的偏导数为：

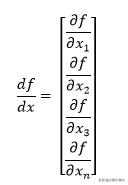
每个变量关于t的偏导数为：

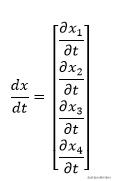
为了构建多元链规则表达式，我们将对两个向量中相似位置的项的乘积求和。正是点积的作用。

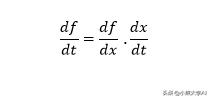
这是我们用于广义形式的多元函数的整洁链规则。

到现在为止，您可能已经注意到，我们的偏导数向量与上一部分中看到的雅可比向量相同。稍作更改，就是我们将其写为行向量。这意味着向量df / dx是函数f的雅可比的横向。

这向我们展示了jacobian如何方便地表示多变量链规则。

接下来，让我们看看链式规则如何作用于两个以上的连接。

举个例子。

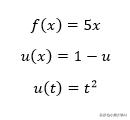
我们还可以通过替换表达式来找到df / dt，例如

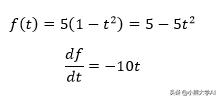
另一种方法是应用两步链规则。

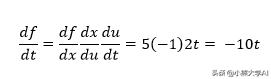
这说明了该方法如何应用于单变量函数链。可以将其扩展到我们可能需要的尽可能多的中间函数。但是这种方法如何适用于多元函数？

让我们来看看。考虑多元函数，

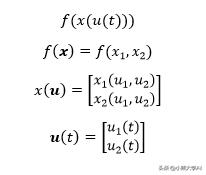
函数f在此将向量x作为输入。同样，向量x是将向量u作为其输入的函数。向量u也是一个以t为输入的函数。t是标量。

请注意，两个标量f和t通过两个中间向量值函数连接在一起。

回到我们与单变量函数相同的表达式，

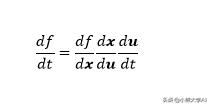
我们之前已经看到，区分其输入x给出雅可比行向量。同样，对标量t求微分给出列向量。对于中间项，我们需要找到两个输入变量中每个输出变量的导数。归结为

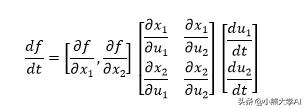
因此，f关于的导数实际上是f的雅可比与x的雅可比和u的派生的乘积。

矩阵的尺寸为(1×1)=(1×2)(2×2)(2×1)，表明乘积是可能的，并且将返回标量。正是我们所期望的！

现在在用于机器学习的微积分第4部分中，我们开始了解线性代数和多变量微积分如何一起发挥作用……

人工神经网络和多变量链规则：

现在让我们谈谈对链规则的理解如何应用于人工神经网络。

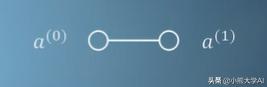
每当我们听到“人工神经网络”这一术语时，就会想到以下图表。我们说圆形是神经元，线是它们之间的连接。

就数学而言，ANN是一种数学函数，其中一些变量作为输入，而某些变量作为输出。这些变量也可以是向量。

将此图转换为数学表达式，我们可以这样：

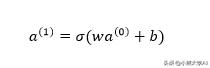
这里的a项是活动，w是权重，b是偏差，sigma是激活函数。

函数sigma是使我们的人工神经网络与人脑关联的原因。在我们的大脑中，神经元通过化学和电刺激从其他神经元接收信息。当所有这些刺激的总和增加时，某个阈值将激活神经元，进而刺激其附近的神经元。

双曲正切函数tanh具有此阈值属性，范围为-1至1。与其他函数一样，tanh具有称为S形的特征。因此，使用sigma来表示它。

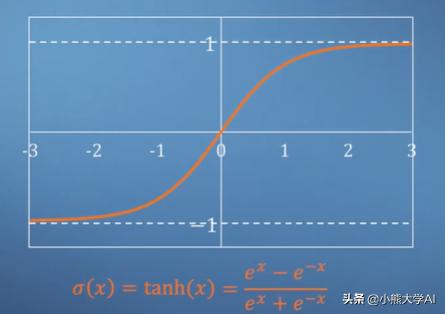
在这一点上，我们简单的神经网络似乎毫无用处。为了使它有趣，或者换句话说，使其能够执行某些工作，我们应该增加一些复杂性，即引入更多的神经元。

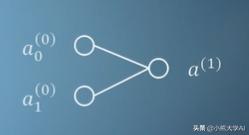
然后我们可以将上面的表达式修改为：

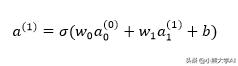
但是随着我们不断增加输入神经元的数量，我们将开始变得混乱。为了将其归纳为n个输入，我们可以执行以下操作：

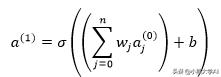
为简化起见，请进一步考虑我们具有向量形式的权重和输入。

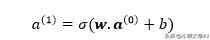
现在，我们的输入向量可以包含任意数量的输入。

将相同的逻辑应用于输出将得出：

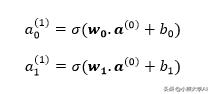
两个输出神经元将具有相同的输入神经元，但权重向量和偏差将不同。

考虑到两个输出是列向量的行，我们可以进一步将这些方程压缩为向量形式，并且可以将两个权重向量保存在权重矩阵中，将两个偏差向量保存在偏差矩阵中。

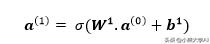
上图显示了具有n个输入和n个输出的单层神经网络如何由我们在上面形成的单个方程表示。在图像下方，我们可以看到工作中的权重和偏差！

神经网络通常在输入和输出之间有一层或多层，我们称之为隐藏层。它们以相同的方式工作，即一层的输出成为下一层的输入。

鉴于此，我们现在具有计算前馈神经网络输出所需的所有线性代数。

但是，要使该神经网络做一些像图像识别这样的工作，我们必须权衡正确的权重和偏差值。现在让我们看看如何使用多元链规则来做到这一点。

多元链规则可帮助我们更新权重和偏差，直到我们的神经网络开始根据给定的训练示例对输入进行分类。

简单地训练神经网络意味着使用一些包含输入值及其相应输出值的标记数据。

例如，训练一个神经网络来识别面部，输入的可能是一些图像像素，而输出可能是面部或者不是面部。

最常用的训练方法是反向传播。它从输出神经元开始，并通过神经网络中的神经元起作用。

考虑一个具有4个输入单元，3个隐藏层单元和2个输出单元的简单神经网络，我们必须计算18个权重和5个偏差的值。使用这些值，我们可以训练我们的网络以正确地将输入与其标签匹配。

最初，权重和偏差设置为某个随机数。可以预期，此时任何输入数据都将给出无意义的输出。

在这里，我们定义了成本函数。成本函数只是我们期望的目标输出与当前未经训练的神经网络输出之间的差平方的总和。

成本和权重值之间的关系可以如下给出：

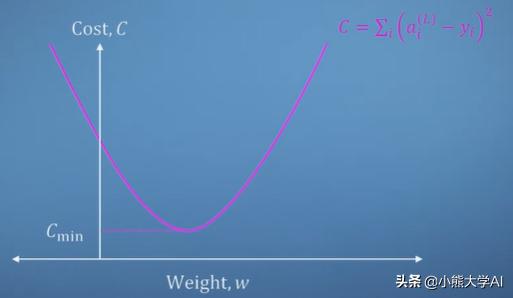
值太大或太小，成本会更高，但在某一特定点，成本最低。

如果使用我们的演算知识，我们能够找到权重的成本梯度，那么我们可以简单地开始朝相反的方向移动。

下图显示梯度为正，增加权重会增加成本，因此我们减小权重以改善神经网络。

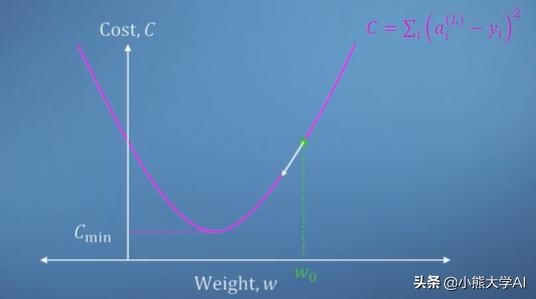
另外，这种情况很简单。我们的成本函数在多个局部极小值的情况下会非常混乱，这使我们的导航变得困难。此外，这里我们仅考虑单个权重。

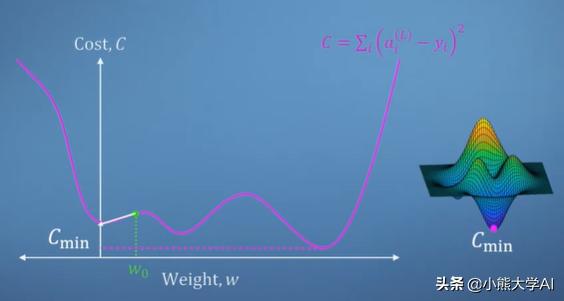
我们对找到最少的多维表面更感兴趣。

回顾我们先前的学习，在这种情况下，我们可以通过结合相关变量的成本函数的偏导数来计算下坡运动的雅可比行列式。

现在，我们可以很容易地写出关于权值或偏差的代价偏导数的链式规则。

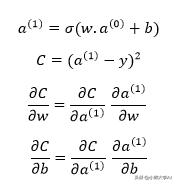
引入另一个项z1将使表达式更方便。z1包含我们的加权激活加偏差值。这有助于我们区分单独选择的特定S型函数。

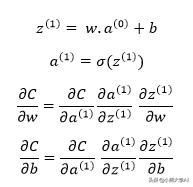
这两条链规则将帮助我们在二维权重偏差空间中导航，同时在一些示例中通过简单的神经网络训练将成本降至最低。

显然，随着神经元数量的增加，这个故事变得更加复杂了，但基本上，我们只是在应用链式规则将权重和偏见联系起来，以最终影响我们训练神经网络的成本。

总结：

最终，在用于机器学习的微积分第4部分中，我们开始看到了实际的微积分。到目前为止，我们还了解到线性代数和微积分构成了机器学习技术的基础。