锯齿波的傅里叶变换_奇妙的傅里叶矩阵之 e^ikt

函数或者信号在各个领域都是被人们广泛研究的课题。而傅里叶级数从时域和频域两个角度对信号进行研究和计算，无论在理论上或者实践中都有重要的意义和价值，很多人都在学习和研究这个理论。

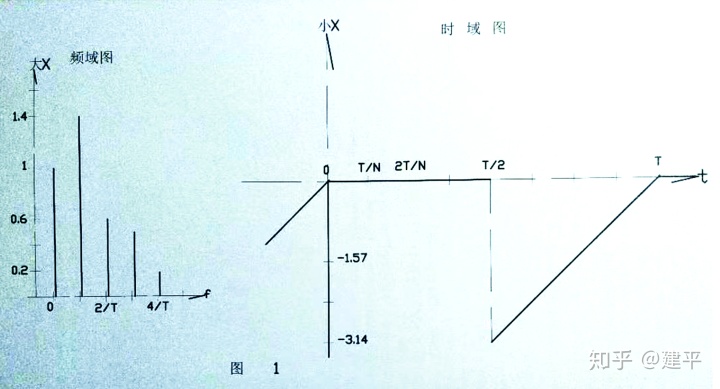
图1所示为一个下锯齿形信号，右面的时域图表示随时间变化的信号波形。其中坐标横轴为时间 t 轴。我们采用离散型函数的研究方法，选取一个周期T的时间作为研究区间，确定一个样本点数N等分周期T，坐标竖轴小x表示出对应于各个时刻 0，T/N, 2T/N,.....nT/N.....(N-1)T/N的信号的振幅值。

左面的频域图则把这个信号看作不同频率三角函数谐波的叠加。坐标横轴为频率 f 轴，0表示信号常量，1/T为基波（与信号本身同频率），2/T为二次谐波......k/T为k次谐波，谐波频率依次递增。坐标竖轴大X表示对应各次谐波的振幅峰值，也就是数学式中各次谐波前面的系数。对于下锯齿形信号，常量部分为1；基波为1.4，强度最大；高频部分渐弱。

离散傅里叶变换(DFT)和逆变换（IDFT)用下面两个数学式表示。

DFT

=

(0

k

N-1)

IDFT

=

(0

n

N-1)

本文规定

=e^i

（有些文章规定

=e^-i

),N为样本点数，k为谐波次数，n表示时刻。这个式子简单明了，但比较抽象。本文采用线性代数里向量，基与坐标，矩阵等概念，力求问题阐述简单易懂。

在线性代数里可以用向量来表示函数或者信号。所谓向量就是n个有次序的数所组成的数组，例如下锯齿形信号在一个周期里的表示，可以用小x的顺序排列实现，[0,0,0,0,-

,-3/4

,-1/2

,-1/4