AAAI 2021 Embedding Heterogeneous Networks into Hyperbolic Space Without Meta-path

文献： 在线链接 🧃 本地链接¹ 🍹 AAAI 2021

摘要

🍍 现有问题

现有异质网络嵌入的两个不足：

1. 目标空间通常是欧几里德空间。然而，许多最近的研究表明，复杂网络可能有双曲隐性结构，这是非欧几里德空间。
2. 方法通常依赖于元路径，需要特定领域的先验知识来进行元路径选择。此外，同一网络上不同的下行任务可能需要不同的元路径来生成特定于任务的嵌入。

提出了一种自引导随机游走方法，该方法不需要元路径，就将异构网络嵌入到双曲空间中。

引言

🍸 引言写作逻辑

1️⃣网络嵌入研究广泛 ⇨ 2️⃣词向量 → DeepWalk → node2vec ⇨ 3️⃣嵌入方法分类：异质网络嵌入、同质网络嵌入 ⇨ 4️⃣异质网络嵌入总结，引出本文向双曲空间的嵌入 ⇨ 5️⃣双曲空间的 $2$ 个优势 ⇨ 双曲空间嵌入的现有研究HHNE的 $3$ 个不足 ⇨ 6️⃣本文方法

双曲空间的 $2$ 个优势

1. 双曲空间对层次结构具有较强的表示能力;

   Hyperbolic space has a stronger representation ability for hierarchical structures;

   Sarkar(2011)表明，树能够以任意低的失真嵌入到二维双曲空间(庞加莱圆盘模型)中。另一方面，Linial等人(1995)表明欧几里德空间不能表示具有低失真的树。相当数量的网络具有层次结构，这使得它们适合嵌入到双曲空间中。

2. 它能够比欧几里德空间更好地表示高阶顶点，这在处理顶点的度服从幂律分布的复杂网络时很重要(即，在有许多大阶的枢纽的情况下)。

   It represents high-degree vertices better than Euclidean space, which is important when dealing with complex networks where the degree of the vertices follow a power-law distribution (i.e., where there are hubs with many large degrees).

HHNE的 $3$ 个不足

就作者所知，提出的将异质网络嵌入到双曲空间的唯一其他方法是HHNE (Wang, Zhang, and Shi 2019)。然而，HHNE也存在以下缺点：

1. 需要元路径来引导随机行走。已有文献表明，元路径的选择高度影响嵌入的质量(Hussein, yang, and Cudré-Mauroux 2018)，且元路径的选择需要领域特定的先验知识，这使得HHNE不容易推广。
2. 即使对于同一网络，针对不同的下游任务，HHNE也需要不同类型的元路径进行训练。
3. HHNE将网络嵌入到庞加莱球模型。但据我们所知，庞加莱球模型上的梯度不能精确计算，需要对指数映射进行一阶近似，称为收缩(retraction)(Bonnabel 2013)。

文章的应对思路

提出了一种自引导随机游走方法。该方法不需要元路径，❗️ 并且在所有域和下游任务中使用很少的非敏感参数 。我们使用双曲面模型来嵌入网络，以避免收缩近似。

Our method does not require meta-paths and uses very few non-sensitive parameters across all the domains and down-streaming tasks.

❗️这里推测作者想要表达 “使用了很少的敏感参数”,但原文中的表述又好像不是,是我翻译错了嘛?

相关研究

同质网络嵌入

除了基于随机行走的方法DeepWalk和node2vec外，LINE (Tang et al. 2015)还提出了用于大规模网络嵌入的方法，能够保持一阶和二阶近似。Cao等人(2015)通过创建GraRep扩展了LINE，该方法在嵌入网络时保留了k步邻近性。他们的模型通过操纵图上定义的不同全局转移矩阵，直接捕捉图中顶点之间k值不同的k步关系信息，而不涉及缓慢和复杂的采样过程。SDNE (Wang, Cui, and Zhu 2016)也是LINE的扩展，它使用半监督深度自编码器模型来捕获网络中的一阶和二阶近似。HOPE (Ou et al. 2016)通过解决一个矩阵分解问题，学习了在有向网络中捕捉非对称高阶邻近性的节点表示，而APP (Zhou et al. 2017)是另一种网络嵌入方法，通过使用Monte Carlo方法来近似非对称根PageRank相似性 (Song et al. 2009)，来捕获非对称邻近性。在双曲线嵌入领域，Nickel等人(2017)提出了一种学习符号数据层次表示的方法(PoincaréEmb);McDonald等人(2019)提出了一种 "瞬移"行走方法来嵌入属性图，Ganea等人(2018)使用双曲锥作为一种启发式方法来嵌入有向无环图。我们之前的工作(Wang et al. 2020)也提出了一种将同构网络节点的结构角色相似度嵌入双曲空间的方法。

异构网络嵌入

为了处理异质网络，metapath2vec (Dong, Chawla, and Swami 2017)通过元路径引导的随机游走扩展了DeepWalk和node2vec。HIN2V ec提出了一种基于不同关系类型和网络结构的多任务学习方法。JUST (Hussein, Y ang，和CudréMauroux 2018)提供了一种随机游走的跳跃/停留 ( Jump/Stay ) 策略，以平衡异质边和同质边。HeteSpaceyWalk (He et al. 2019)首先将元路径引导的随机游走形式化为一个高阶马尔可夫过程，然后利用一种高效的随机游走，他们称之为异质个性化空间随机游走。AspEm (Shi et al. 2018a)提出了网络的方面的概念 (the concept of aspects in networks)，基于HIN的多个方面，保留HIN的语义信息。PTE (Tang, Qu, and Mei 2015)通过边的类型将一个网络分解为多个二部网络，从单跳邻域学习表示，HEER (Shi et al. 2018b)通过考虑类型的亲密度将其扩展。在双曲线嵌入领域，目前仅有一种异构嵌入方法，即HHNE (Wang, Zhang, and Shi 2019)，该方法利用元路径引导的随机漫步扩展metapath2vec，将节点嵌入到aPoincaré ball中。随着图神经网络(GNN)的发展，许多方法，如R-GCN (Schlichtkrull等人，2018年)、HGT (Hu等人，2020年)、HAN (Wang等人，2019年)和HetGNN (Zhang等人，2019年)将GNN用于异构网络。最后，知识库是一种特殊的异质网络。许多基于关系学习的知识库方法，如TransE (Bordes et al. 2013)、TransH (Wang et al. 2014)、RotatE (Sun et al. 2019)、DistMult (Y ang et al. 2014)、NKGE (Wang et al. 2018)和SACN (Shang et al. 2019)已被提出。

框架

异质网络HIN

异质网络 $G=(V,E,T)$ ，包含映射函数 $\varphi (v):V\to T_V$ 和 $\phi (e):E\to T_E$ ， $T_V,T_E$ 分别表示节点和边的类型集合，且 $\left|T_V\right|+\left|T_E\right|>2$ 。网络嵌入目的是以无监督的方式学习一个 $d$ 维的双曲空间 $\mathrm{X}\in {\mathbb{H}}^{|V|\times d},d\ll |V|$ 。

自引导随机游走

首先回顾元路径引导的随机游走：元路径用于异质图嵌入，因为HIN上的随机游走偏向于高频节点类型(highly visible types of nodes)。这意味着由随机游走生成的序列具有节点的偏态分布 (skewed distribution)，高频节点类型被过度表达(over-represented)。从这些序列中学习到的节点嵌入也将偏向于高频域(highly visible domains)。因此，使用元路径指导随机游走，以克服该问题(Hussein,Yang，and Cudré-Mauroux 2018)。

文章提出的自引导随机游走方法，可以在下一步的游走中自适应地改变每个节点类型的概率，并自动平衡上下文中的域分布。

Self-guided random walk method can adaptively change the probability of each node type in the next walk step and automatically balance the distribution of domains in the context.

对任意 $1⩽i<k$ ， $G$ 上的自引导路径是一个节点序列 $⟨v_1,v_2,\cdots ,v_k⟩$ ，满足 $⟨v_i,v_{i+1}⟩\in E$ ，且节点类型 $\varphi \left(v_i\right)$ 出现 ${\mathcal{N}}_{\varphi \left(v_i\right)}$ 次。不同标准随机游走那样，以等概率游走到所有的邻居节点，文章为类型 $\varphi$ 定义了一个修正概率：
$$\frac{e^{-{\mathcal{N}}_{\varphi }}}{{\sum }_{{\varphi }^{\prime }\in T_V}{e}^{-{\mathcal{N}}_{{\varphi }^{\prime }}}}$$
对于游走序列 $⟨v_1,v_2,\cdots ,v_k⟩$ ，分数约简(fraction reduction)后， $k+1$ 步的转移概率可以被正则化为：
p ( v k + 1 ∣ ⟨ v 1 , v 2 , ⋯   , v k ⟩ ) = e − N ϕ v k + 1 ∣ { ϕ v k + 1 = ϕ v i ∣ ( v k , v i ) ∈ E } ∣ ∑ ( v k , v j ) ∈ E e − N ϕ v j ∣ { ϕ v j = ϕ v i ∣ ( v k , v i ) ∈ E } ∣ p\left(v_{k+1} \mid\left\langle v_{1}, v_{2}, \cdots, v_{k}\right\rangle\right)=\frac{\frac{e^{-\mathcal{N}_{\phi_{v_{k+1}}}}}{\left|\left\{\phi_{v_{k+1}}=\phi_{v_{i}} \mid\left(v_{k}, v_{i}\right) \in E\right\}\right|}}{\sum\limits_{\left(v_{k}, v_{j}\right) \in E} \frac{e^{-\mathcal{N}_{\phi_{v_j}}}}{\left|\left\{\phi_{v_{j}}=\phi_{v_{i}} \mid\left(v_{k}, v_{i}\right) \in E\right\}\right|}} p(vk+1​∣⟨v1​,v2​,⋯,vk​⟩)=(vk​,vj​)∈E∑​∣{ϕvj​​=ϕvi​​∣(vk​,vi​)∈E}∣e−Nϕvj​​​​∣{ϕvk+1​​=ϕvi​​∣(vk​,vi​)∈E}∣e−Nϕvk+1​​​​​
通过这种方式，所有类型的节点都将在上下文中得到平衡。

双曲空间嵌入

首先简要介绍了双曲面模型及其梯度，然后解释了如何根据自引导随机游走的结果训练嵌入向量。

在几何学中，双曲面模型（hyperboloid model，/haɪˈpɜːbəˌlɔɪd/），也称为闵可夫斯基模型（Minkowski model）或洛伦兹模型（Lorentz model）。n-维双曲空间的双曲面模型与凯莱-克莱因模型密切相关：两者都是射影模型。

双曲空间的曲率为负。有多种模型可以用来表示双曲空间，每一个都有不同的优点。庞加莱球模型是用于低维嵌入向量可视化的最佳模型。由于Klein模型计算效率高，常用于 Einstein midpoints 的计算。双曲面模型给出了梯度下降公式的封闭形式(closed-form)。因此，文章采用双曲面模型，以方便计算梯度。下面将讨论定义双曲面模型及其梯度所需的几个定义(Wilson and Leimeister 2018)。

🌴定义1：闵可夫斯基内积(Minkowski inner product)
$$⟨x,y{⟩}_{n:1}=x_1{y}_1+x_2{y}_2+\cdots +x_n{y}_n-x_{n+1}{y}_{n+1}$$
闵可夫斯基内积不是传统的内积，因为它不是正定的。

🍐定义2：双曲模型(Hyperboloid model)
$${\mathbb{H}}^n=\left\{x\in {\mathbb{R}}^{n:1}\mid ⟨x,x{⟩}_{n:1}=-1,x_{n+1}>0\right\}$$
${\mathbb{R}}^{n:1}$ 代表 $\text{ambient Minkowski space}$，一个简单的双曲模型实例是旋转的双曲面： ${\mathbb{H}}^2=\left\{x\in {\mathbb{R}}^3\mid x_1^2+x_2^2-x_3^2=-1,x_3>0\right\}$

⛺定义3：双曲距离(hyperbolic distance)

点 $x$ 和 $y$ 之间的双曲距离定义为：
$$d_{{\mathrm{H}}^n}(x,y)={\cosh }^{-1}\left(-⟨x,y{⟩}_{n:1}\right)$$
可以计算在 ${\mathbb{R}}^{n:1}$ 中双曲距离函数的梯度：
$$\begin{array}{rl}abl{a}_x^{{\mathbb{R}}^{n:1}}d(x,y)& =abl{a}_x^{{\mathbb{R}}^{n:1}}{\cosh }^{-1}\left(-⟨x,y{⟩}_{n:1}\right)\\ & =-\frac{1}{\sqrt{⟨x,y{⟩}_{n:1}^2-1}}abl{a}_x^{{\mathbb{R}}^{n:1}}⟨x,y{⟩}_{n:1}\\ & =-\frac{y}{\sqrt{⟨x,y{⟩}_{n:1}^2-1}}\end{array}$$
🍹定义4：切线空间(tangent space)

点 $x\in {\mathbb{H}}^n$ 的切线空间 $T_x{\mathbb{H}}^n$ 是满足下式的点的集合：
$$T_x{\mathbb{H}}^n=\left\{u\in {\mathbb{R}}^{n:1}\mid ⟨u,x{⟩}_{n:1}=0\right\}$$
从 $\text{ambient space}$ ${\mathbb{R}}^{n:1}$ 到切线空间 $T_x{\mathbb{H}}^n$ 的投影是：
$${\Pi }_x(u)=u+⟨u,x{⟩}_{n:1}x\text{\hspace{1em}(7)}$$
🍐定义5：指数映射(exponential map)

指数映射是将一个向量从切线空间映射到双曲面流形(hyperboloid manifold)的一种常用方法。对于 $u\in T_x{\mathbb{H}}^n$ ，其指数映射为：
$$\cosh \left(\sqrt{⟨u,u{⟩}_{n:1}}\right)x+\sinh \left(\sqrt{⟨u,u{⟩}_{n:1}}\right)\frac{u}{\sqrt{⟨u,u{⟩}_{n:1}}}\text{\hspace{1em}(8)}$$
基于以上定义，当计算给定函数 $f$ 的梯度时，计算其在环境空间(ambient space)中的梯度 $abl{a}_x^{{\mathbb{R}}^{n:1}}f$ ，接下来，使用$公式7$ 将其投影到切空间中，并对我们使用 $公式8$ 得到的向量应用指数映射。

设计损失函数，以评估嵌入向量：

参照HEAT (McDonald and He 2019)，在生成自引导随机游走序列之后，使用滑动窗口检查所有序列，将窗口内出现的节点对添加到 $\text{multi-set}$ $\mathcal{P}$ 中，作为所有用于训练的正样本对。直观上看，两个节点之间的距离越远，存在连边的概率就越小。假定连边概率应该正比于 $e^{-d_{{\mathrm{H}}^n}^2\left({\mathbf{e}}_u,{\mathbf{e}}_v\right)}$ ，其中， $e_u$ 和 $e_v$ 是节点 $u$ 和 $v$ 的嵌入向量。结合负采样技术能够轻松处理大型网络。损失函数由下式给出：
$$\mathcal{L}=-\frac{1}{|\mathcal{P}|}\sum _{(u,v)\in \mathcal{P}}\log \frac{e^{-d_{{\mathrm{H}}^n}^2\left({\mathbf{e}}_u,{\mathbf{e}}_v\right)}}{\sum _{v^{\prime }\in \mathcal{M}(u)}{e}^{-d_{{\mathrm{H}}^n}^2\left({\mathbf{e}}_u,{\mathbf{e}}_{v^{\prime }}\right)}}$$
上式中，对于给定的节点 $v$ ， M ( u ) : = { v } ∪ { w ∣ ( u , w ) o t i n P } \mathcal{M}(u):=\{v\} \cup\{w \mid(u, w) otin \mathcal{P}\} M(u):={v}∪{w∣(u,w)otinP} 包括两个部分：一是节点 $v$ ；二是负采样集。节点 $w$ 被选入负采样集 $\mathcal{M}(u)$ 的概率正比于完整样本集 $\mathcal{P}$ 中节点 $w$ 出现的频率。由于已经获得 ${\mathbb{R}}^{n:1}$ 中距离函数的梯度，以及将其投射到双曲面上的方法，因此用链式法则可以很容易地计算出损失函数的梯度。

实验

网络重构

网络重构任务测试了嵌入方法保持网络原始结构的能力。即从整个网络中学习到的嵌入向量中恢复出网络的结构。为了检验所提方法，文章使用两个节点类型之间的所有边作为正集，而所有非边作为负集。文章使用节点嵌入之间的距离(在双曲面上)，通过采用距离阈值，来预测两个节点之间是否存在链接，从而得到一个AUC评分。

We use the distances between node embeddings (on the hyperboloid) to get an AUC score by thresholding on different distance values for predicting whether a link exists between two nodes.

链接预测

链接预测任务测试嵌入方法预测未知网络结构的能力。对于每一种类型的关系，我们随机地从网络中删除20%的边，而不增加节点 (connected components) 的数量，然后基于网络学习节点的嵌入向量。在测试中，所有被移除的边都被用作正集，而负集则通过随机采样相同数量的非边来创建。AUC的计算方式与网络重构任务相同。

参数敏感性分析

批处理大小、上下文大小(context size)、每个节点的随机游走次数、随机游走长度、负样本数量

context size - The window size used for collecting the positive samples.
negative samples - The number of negative samples per positive sample.

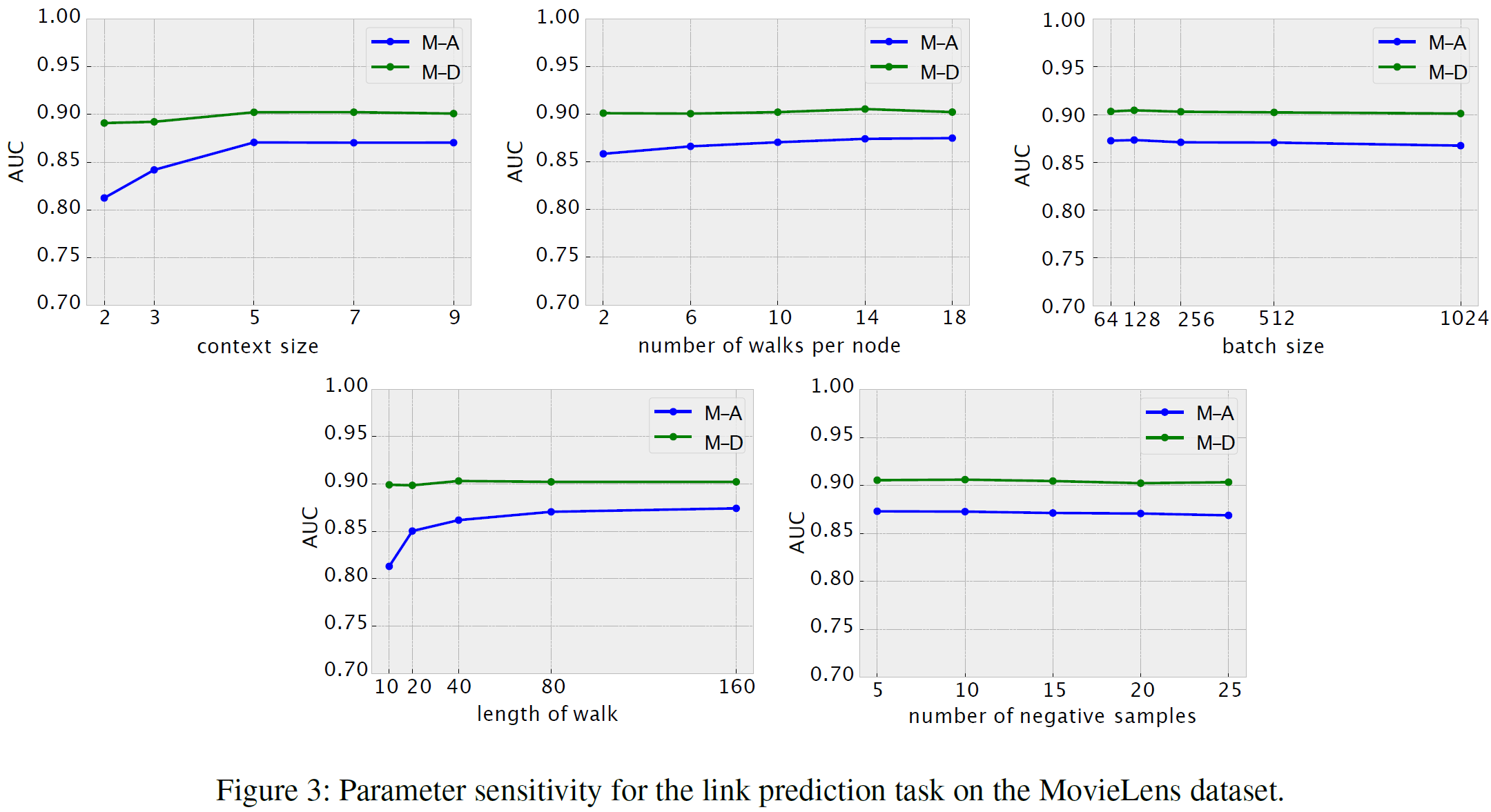
总的来说，模型对参数不敏感。通常情况下，上下文越大，邻域信息的表示越好，而行走长度越长，则自引导随机游走能够为每种类型的节点生成更均衡的节点序列。

Generally, a larger context enables a better representation of neighbourhood information, and a longer length of walk enables the self-guided random walk to generate more balanced node sequences for each type of node.

附录

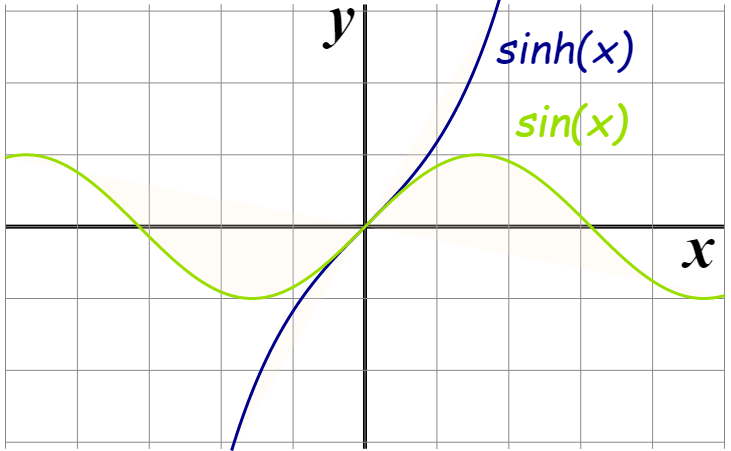
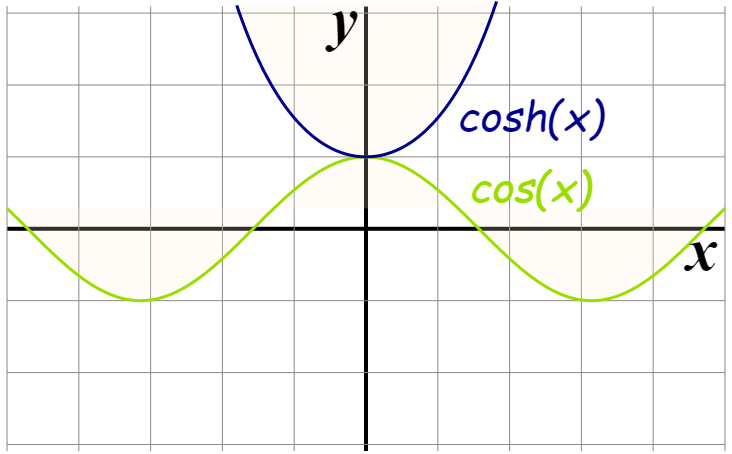
双曲函数

$\sinh (x)=\frac{e^x-e^{-x}}{2}$	$\cosh (x)=\frac{e^x+e^{-x}}{2}$	$\tanh (x)=\frac{\sinh (x)}{\cosh (x)}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$

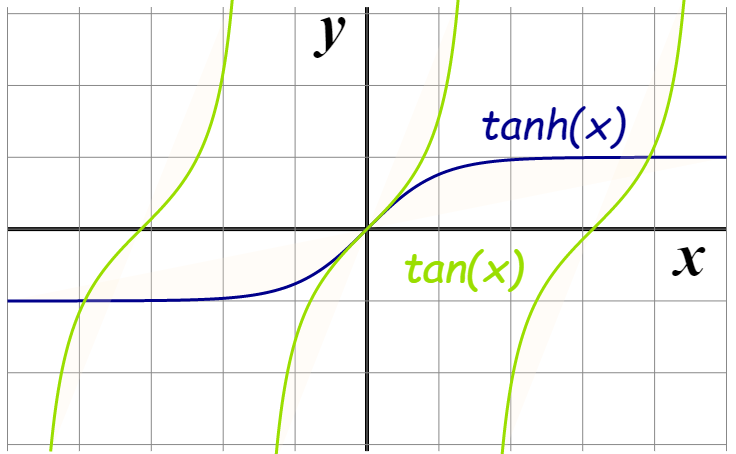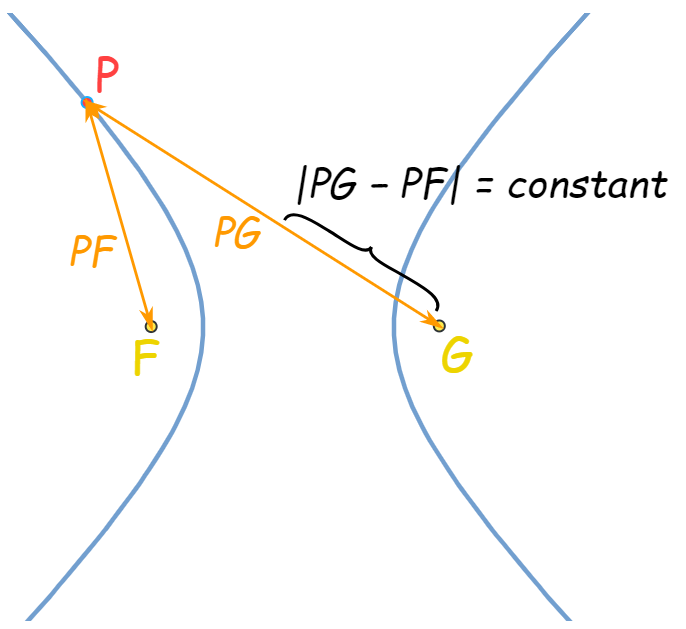
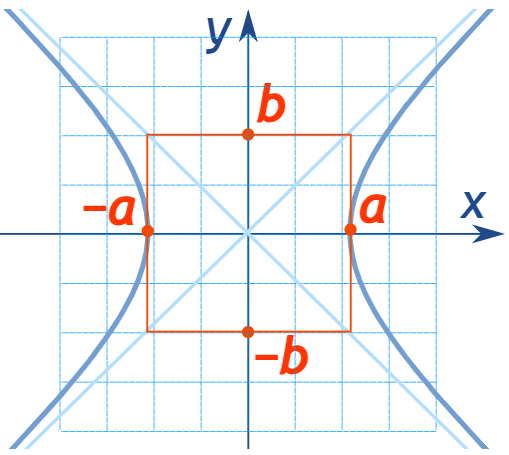
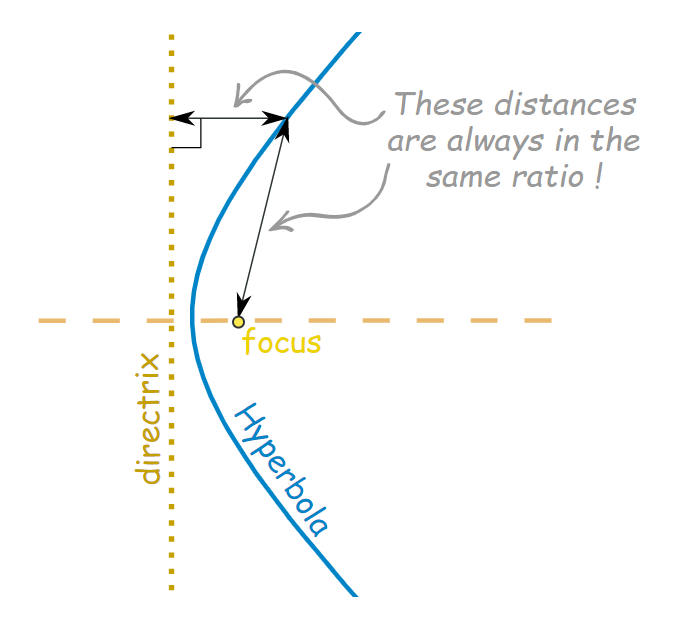
⭐双曲线 hyperbola [haɪ’pɜ:bələ]

$|PF-PG|=\text{ constant }$	$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$	Eccentricity $e=\frac{c}{a}=\frac{\sqrt{a^2+b^2}}{a}$

🌟为什么叫双曲函数？ Why the Word “Hyperbolic” ?

Because it comes from measurements made on a Hyperbola:

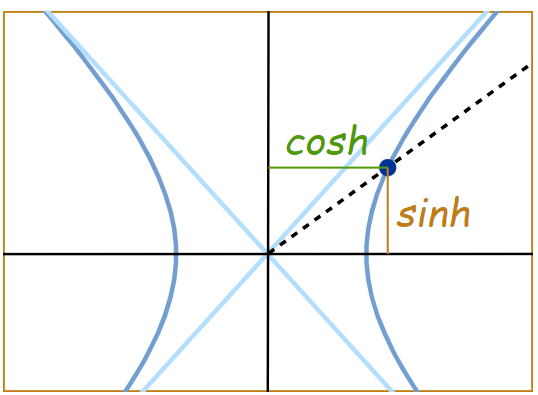
直观上理解不同类型的空间

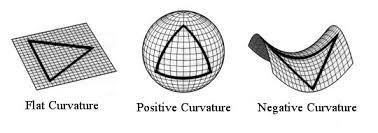
双曲空间, 相比较于欧几里得空间的不同是，其常曲率为负数，而我们所常见的欧几里得空间的曲率为0。

Contrasting triangles in Euclidean, elliptic, and hyperbolic spaces

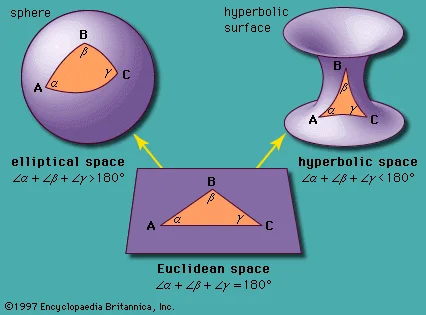
双曲空间模型实例

参考：集智百科–双曲空间模型 、欧氏空间到双曲空间

莱布尼茨首先提出了跟踪曲线的问题。如上面的动画所展示。考虑水平地面上有一个物体，你用一根长长的细杆推动兼或拖拉着它。细杆的长度固定，一边连接着物体，而且连接处可以自由转动，另一端则被你手牵动着。当你沿着 $y=0$ 这条直线匀速直线往前走的时候，那么这个物体在水平地面上运动后形成的轨迹就被称为跟踪曲线Tractrix。采用曲线的弧长作为参数，来列出该曲线的参数方程。我们设从 $x=0$ 点出发的曲线弧长 $s$ 为自变量，那么可以知道曲线的参数方程就变为：
$$\begin{array}{rl}& x=\mathrm{arccosh}{e}^s-\sqrt{1-e^{-2s}}\\ & y=e^{-s}\end{array}$$
让跟踪曲线绕着它的渐近线（ $y=0$ 这个数轴）转一圈，形成的曲面就是一个满足曲率为$－1$ 的双曲平面，该曲面被称为Tractricoid（旋转跟踪曲面），也被称为伪球面 pseudosphere。如下图所示：

可以用弧长以及旋转的角度作为基本参数，写出跟踪旋转曲面的参数方程：
$$\begin{array}{rl}& x=\mathrm{arccosh}{e}^s-\sqrt{1-e^{-2s}}\\ & y=e^{-s}\cos \theta \\ & z=e^{-s}\sin \theta \end{array}$$
其中 $s$ 就是跟踪曲线上的物体从开始走过的弧长， $\theta$ 就是曲线从开始绕着 $y＝0$ 旋转的角度（如下图）。

庞加莱圆盘模型

几何中，庞加莱圆盘模型（Poincaré disk model），也叫共形圆盘模型（conformal disk model），是一个 n-维双曲几何模型。几何中的点对应到 n 维圆盘（或球）上的点，几何中的 “直线”（准确地说是测地线）对应到任意垂直于圆盘边界的圆弧或是圆盘的直径。

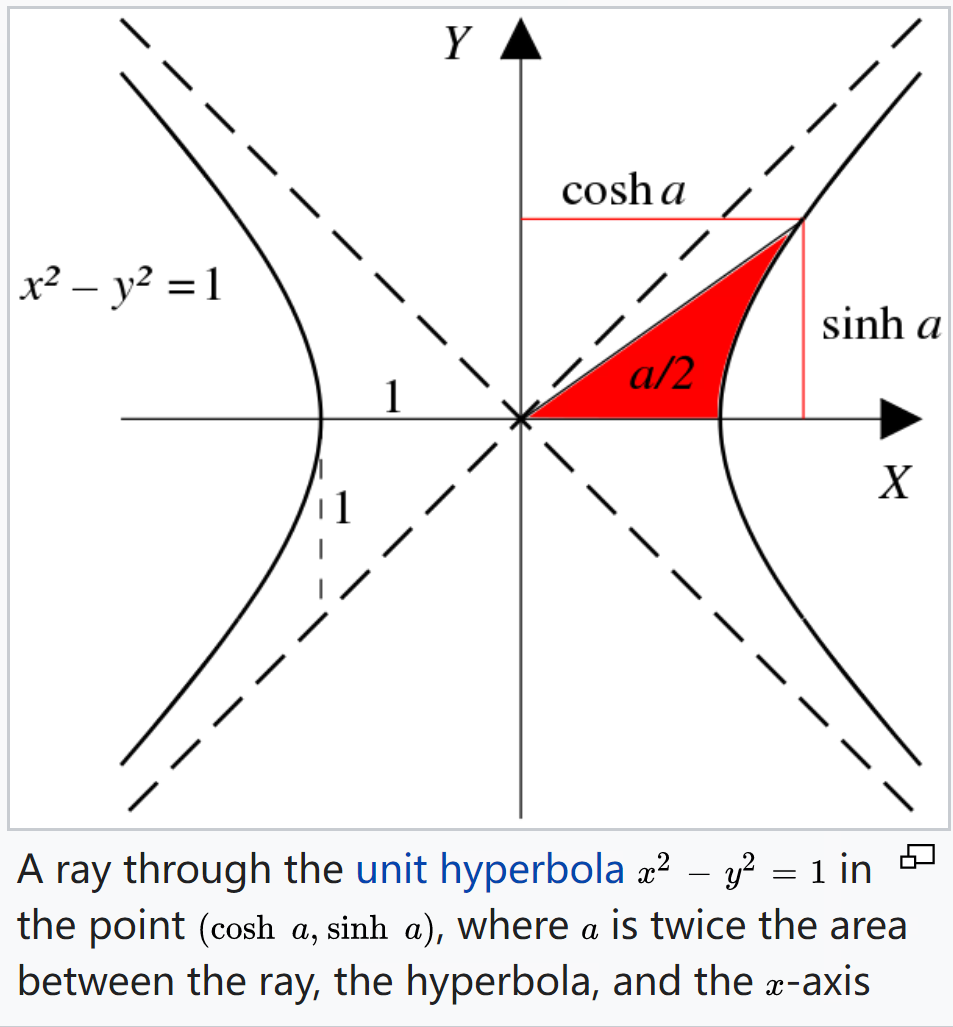Inverse hyperbolic functions

什么是测地线

测地线（英语：Geodesic）又称大地线或短程线，数学上可视作直线在弯曲空间中的推广；在有度规定义存在之时，测地线可以定义为空间中两点的局域最短路径。测地线（英语：geodesic）的名字来自对于地球尺寸与形状的大地测量学（英语：geodesy）。

In geometry, a geodesic ([ˌdʒiːəˈdɛsɪk, ] is commonly a curve representing in some sense the shortest path (arc) between two points in a surface, or more generally in a Riemannian manifold. The term also has meaning in any differentiable manifold with a connection. It is a generalization of the notion of a “straight line” to a more general setting.

The noun geodesic and the adjective geodetic come from geodesy, the science of measuring the size and shape of Earth, while many of the underlying principles can be applied to any ellipsoidal geometry. In the original sense, a geodesic was the shortest route between two points on the Earth’s surface. For a spherical Earth, it is a segment of a great circle (see also great-circle distance). The term has been generalized to include measurements in much more general mathematical spaces; for example, in graph theory, one might consider a geodesic between two vertices/nodes of a graph.

---

1. D:\论文\2021\Conference Paper\2021-Embedding heterogeneous networks into hyperbolic space without meta-path-Thirty-fifth AAAI conference on artificial intelligence, AAAI 2021, february 2-9, 2021.pdf ↩︎