高斯模型混合模型–理论上可以拟合任意概率密度分布

高斯混合模型

  给定变量 $x$ 的有限个观测数据 $x_1,x_2,x_3,\cdots ,x_n$，对变量 $x$ 的概率分布 $p(x)$ 进行建模的过程称为对变量 $x$ 的密度估计，高斯混合模型（Gaussian Mixture Model，GMM）是一种得到了广泛使用且非常有效的密度估计方法，高斯混合模型是用来表示在总分布中含有 $K$ 个高斯分布的概率模型，各个高斯分布称为总分布的子分布。混合高斯模型在计算观测数据在总体分布中的概率时，不需要观测数据提供关于子分布的信息。

  高斯分布，也称正态分布，是自然界中广泛存在的一种数据分布形式，其概率密度函数公式如 $\text{href}$ 所示

$$N\left(x\mid \mu ,{\sigma }^2\right)=\frac{1}{\sqrt{2{\sigma }^2\pi }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}\text{\hspace{1em}(1.1)}$$
其中，参数 $u$ 表示变量 $x$ 的期望，参数 $\sigma$ 表示变量 $x$ 的标准差，更一般的情况下，当变量是多维数据时，即 $\mathbf{x}$ 的维度 $d>1$ 时，多元高斯分布的概率密度函数如 $\text{href}$ 所示：

$$N(\mathbf{x};\mathbf{\mu },\Sigma )=\frac{1}{\sqrt{(2\pi {)}^d\det (\Sigma )}}\exp \left[-\frac{1}{2}(\mathbf{x}-\mu ){\Sigma }^{-1}(\mathbf{x}-\mu {)}^T\right]\text{\hspace{1em}(1.2)}$$
其中，$\mathbf{\mu }$ 是一个 $d$ 维向量，代表了 $\mathbf{x}$ 各个维度的的数学期望，$\Sigma$ 是一个 $d\times d$ 的矩阵，表示了变量 $\mathbf{x}$ 各个维度之间的协方差矩阵。高斯混合模型可以看作 $K$ 个高斯分布的组合，其概率分布形式如 $\text{href}$ 所示：

$$P(\mathbf{x}\mid \theta )=\sum _{k=1}^K{\alpha }_k\varphi \left(\mathbf{x}\mid {\theta }_k\right)\text{\hspace{1em}(1.3)}$$
其中，${\alpha }_k⩾0$ ，$\sum _{k=1}^K{\alpha }_k=1$ ，$\mathbf{\theta }=({\alpha }_1,{\alpha }_2,\dots ,{\alpha }_K,{\theta }_1,{\theta }_2,\dots ,{\theta }_K)$ 表示GMM模型的参数，${\mathbf{\theta }}_k$ 表示GMM第 $k$ 个高斯分布的参数，当 $\mathbf{x}$ 维度为1时，${\mathbf{\theta }}_k=({\mu }_k,{\sigma }_k^2)$ ，$\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 由公式 $\text{href}$ 给出；当 $\mathbf{x}$ 维度大于1时，${\mathbf{\theta }}_k=({\mathbf{\mu }}_{\mathbf{k}},{\Sigma }_k)$ ，$\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 由公式 $\text{href}$ 给出。对于GMM模型的观测数据 ${\mathbf{x}}_i,i=1,2,3\dots ,n$ ，可以认为是经过两个采样步骤生成的：第一步，按照概率 ${\alpha }_k$ 选择第 $k$ 个高斯分布 $\varphi (\mathbf{x}|{\mathbf{\theta }}_k)$ ，第二步，按照第 $k$ 个高斯分布 $\varphi (\mathbf{x}|{\mathbf{\theta }}_k)$ 采样生成观测数据 ${\mathbf{x}}_i$ ，这里需要重点理解的是，我们并不知道观测数据 ${\mathbf{x}}_i$ 来自于哪个高斯分布，记 ${\omega }_{i,k}\in [1,2,3\dots ,K]$ 表示第 $i$ 个观测数据 ${\mathbf{x}}_i$ 来自第 $k$ 个高斯分布的概率，${\omega }_{i,k}$ 是未知的，一般将其称为隐变量。下面将介绍利用期望极大算法估计GMM模型参数的思路。

  期望极大（Expectation Maximum，EM）算法是1977年由Dempster等人¹ 总结提出的，EM算法是含有隐变量的概率模型参数的极大似然估计法。关于EM算法本身正确性及收敛性的证明可以参考文献² ，本文只介绍利用EM算法估计GMM模型参数的简要思路：

步骤 1：赋予GMM模型参数初值 ${\mathbf{\theta }}^0$ ，初值的选择是任意的，但需要注意的是，EM算法只能收敛到局部最优解，所以EM算法对初值是敏感的。

步骤 2：利用当前GMM的模型参数为 ${\mathbf{\theta }}^t$，求隐变量 ${\omega }_{i,k}$ 的期望。

当 ${\mathbf{\theta }}^t$ 给定时，对于 $\text{href}$ 而言， $K$ 个高斯分布 $\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)$ 都是确定的，因此可以求出观测数据 ${\mathbf{x}}_i,i=1,2,3\dots ,n$ 属于第 $k$ 个高斯分布的概率，如 $\text{href}$ 所示：

$${\omega }_{i,k}^t=\frac{{\alpha }_k^t\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)}{\sum _{k=1}^K{\alpha }_k^t\varphi \left(\mathbf{x}\mid {\mathbf{\theta }}_k\right)}\text{\hspace{1em}(1.4)}$$
步骤 3：基于当前的隐变量 ${\omega }_{i,k}$ 的值，利用极大似然估计法更新GMM的模型参数为 ${\mathbf{\theta }}^{(t+1)}$ 。

当隐变量 ${\omega }_{i,k}$ 给定时，此时估计GMM模型参数就退化为一个不含隐变量的概率模型参数估计问题，可以利用极大似然估计法求得当前步骤模型参数的相合估计量，如下式所示：
$$\begin{array}{rl}& \text{当}d=1\text{时},\{\begin{array}{l}{\alpha }_k^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}^t}{N}\\ \\ {\mu }_k^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}^t{x}_i}{\sum _{i=1}^N{\omega }_{i,k}^t}\\ \\ {\left({\sigma }_k^2\right)}^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}{\left(x_i-{\mu }_k^{t+1}\right)}^2}{\sum _{i=1}^N{\omega }_{i,k}}\end{array}\\ & \text{当}d>1\text{时},\{\begin{array}{l}{\alpha }_k^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}^t}{N}\\ \\ {\mathbf{\mu }}_k^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}^t{\mathbf{x}}_i}{{\sum }_i{\omega }_{i,k}^t}\\ \\ {\Sigma }_k^{t+1}=\frac{\sum _{i=1}^N{\omega }_{i,k}^t\left({\mathbf{x}}_i-{\mathbf{\mu }}_k^{t+1}\right){\left({\mathbf{x}}_i-{\mathbf{\mu }}_k^{t+1}\right)}^T}{\sum _{i=1}^N{\omega }_{i,k}^t}\end{array}\end{array}$$

为什么高斯模型混合模型（GMM）理论上可以拟合任意概率密度分布呢？

百科搬运工

中文说明

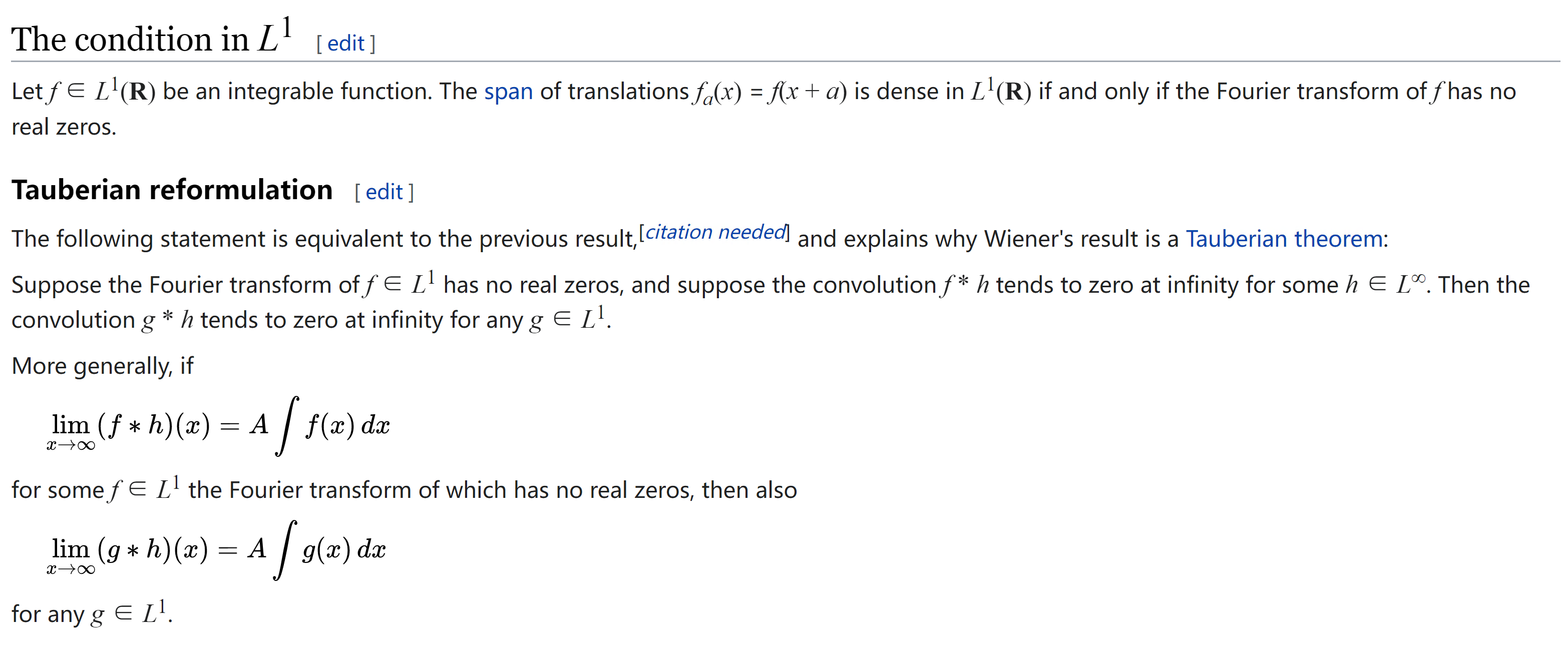
  定理实际上比GMM可以逼近任何概率分布条件要强，因为只用了平移。另外因为高斯函数的积还是高斯函数，似乎用Stone-Weierstrass定理也可以。选用高斯分布的理由其实有很多，一方面因为中心极限定理，生活中高斯分布非常多，另一方面，它实在是太好算了。其实第二个理由更充分，毕竟对任意的概率分布不可能总是高斯逼近是最好的。不过一般的GMM效果都不错。

你可能需要的参考文献

分别对应百科第一段中引用的两个参考文献：

[1] Meir, A., 1963. Tauberian theorems. Israel Journal of Mathematics 1, 29–36. https://doi.org/10.1007/BF02759798
[2] Rudin, W., 1991. Functional analysis, 2nd ed, International Series in Pure and Applied Mathematics. New York : McGraw-Hill.

---

1. Dempster, A.P., Laird, N.M., Rubin, D.B., 1977. Maximum likelihood from incomplete data via the EM algorithm. JOURNAL OF THE ROYAL STATISTICAL SOCIETY, SERIES B 39, 1–38. ↩︎

2. 李航, 《EM算法及其推广》, 收入 统计学习方法, 第2版., 清华大学出版社, 2019, 页 175–183. ↩︎