提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
摘要
复杂网络是具有小世界、聚类和幂律分布特征的网络。关键扩展器(重要节点)的发现作为复杂网络的重要研究方向之一,主要用于识别在网络结构和功能中起关键作用的节点。重力模型是识别影响者的一种特殊方法,但是这种方法涉及一个开放的问题,即如何确定交互的范围(例如节点质量和影响力计算)。此外,在传统方法中,质量仅以节点的度数来表示。为了解决上述问题,本文提出了一种基于精确半径和数值信息的有效重力模型。精确计算出截断半径,并将代表节点传播能力的价值信息修改为大众。(简而言之,节点的影响范围和价值得分是根据每个节点的属性和网络中邻居节点的交互来计算的)。与其他类似方法和最先进的措施相比,本文方法的合理性和优越性通过对11个真实世界网络的6个实验进行了证明。
一、识别有影响力节点的经典方法模型
首先回顾在复杂网络中识别重要传播者的一些基本方法。
1.1 度中心性
节点的重要性取决于邻居的数量。给定一个网络,归一化 DC定义如下

Ki表示为节点的度数。
1.2 接近中心性
一个节点与所有其他节点的距离之和需要计算接近中心度。和较小的节点意味着它更接近所有其他节点,这表明该节点的重要性更高。归一化的CC本质上是距离的倒数,定义如下。

其中 n 表示网络中的节点数,dij 表示节点 i 和节点 j 之间的最短路径距离。
1.3 中介中心
在中介中心性中,节点的重要性是通过该节点的最短路径的数量来衡量的。一个节点多次出现在节点之间的最短路径中意味着它具有很大的影响力。反映节点作为桥梁重要性的BC[19]定义如下。

其中分子用于表示节点 u 和节点 j 之间经过节点 i 的最短路径数,节点 u 和节点 j 之间的最短路径数用分母 表示。
1.4 特征向量中心性
特征向量中心性是衡量节点间传输影响和连通性的一种方法,考虑了邻居节点的重要性。 EC 认为来自关键节点的链接比来自琐碎节点的链接更有价值。给定图的邻接矩阵,特征向量中心性 [20] 定义如下。

其中 x 表示矩阵 A 的特征值,namuta对应的特征向量。
1.5 PageRank 中心性
PageRank中心性[21]是一种基于网页之间的相互超链接计算的技术,用于衡量特定网页在搜索引擎索引中相对于其他网页的重要性。一个页面的重要性取决于所有只引用它的页面的重要性。在初始阶段,网页通过链接关系构建一个网络地图,每个页面都被赋予相同的PageRank值。然后每个页面将其当前的PageRank值平均分配给该页面包含的out-links,从而使每个链接获得相应的权重。最后,每个页面将所有进入该页面的链接传入的权重相加(如下),就可以得到一个新的PageRank分数。当每个页面得到更新后的PageRank值时,就完成了一轮PageRank计算。上述过程不断迭代,稳定下来就是最终结果。其中一个页面的PR值用以下形式表示

其中α表示到达某个页面并继续向后浏览的概率,Oi表示所有链接到第i个网页的网页的集合。网页 j 的链接数用 L(j)表示,N 表示网页的总数。
二、重力中心模型经典方法
2.1 重力中心模型
基于万有引力定律的重力中心方法同时考虑了局部和全局信息。在GC中,一个节点的度相当于质量,取两个节点之间的最短距离作为距离。节点 i 的 GC [30] 定义如下。

其中 ki 和 kj 分别表示节点 i 和节点 j 的度数,dij 表示节点 i 和节点 j 之间的最短距离。引入截断半径 R=0.5(平均距离)来解决噪声和耗时问题,其中d表示平均路径长度。
2.2 加权重心模型
加权重心模型通过考虑节点的权重来修正 GC。引入特征向量概念的WGC[31]方法定义如下。
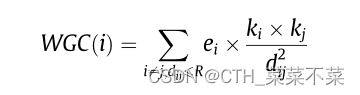
其中 dij 表示为节点 i 和节点 j 之间的最短距离。节点 i 和节点 j 的度数用 ki 和 kj 表示,ei代表最大特征值的归一化特征向量的第 i 个值。
2.3 广义重心模型
在广义重力中心性模型中,节点的质量由扩散能力表示。节点的传播能力取决于度数和聚集系数。节点 i 的 GGC [33] 定义如下



spi表示节点 i 的通信能力,阿尔法是一个自由参数,Ci是聚集系数,在实际应用中可以灵活调整。 dij 表示节点 i 和节点 j 之间的距离,R表示截断半径;
三、 两项最先进的措施
3.1 局部信息维度
- 熵的的定义:

- 香农熵。用于测量局部信息维度中每个框的节点数。 LID [22] 考虑了中心节点周围的局部结构特征,定义如下


其中 d 表示导数的符号,l 表示框的大小,术语pi(l)是信息包含在具有给定框大小 l 的中心节点 i 的 框内的概率;ni(l)表示方框中的节点数,N 表示网络中的节点总数。
3.2 模糊局部维度
- 模糊局部维度使用模糊集(把待考察的对象及反映它的模糊概念作为一定的模糊集合,建立适当的隶属函数,通过模糊集合的有关运算和变换,对模糊对象进行分析) [35] 来研究距中心节点 [36] 不同距离的节点。节点的贡献受距离的影响,距离是通过模糊集在FLD上测得的。关注每个节点的局部属性的
FLD [23] 定义如下。
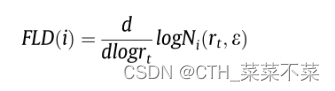








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 5472
5472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








