论文阅读 |【Robotics】Monte Carlo tree search with spectral expansion for planning with dynamical systems

m0_61750953

已于 2024-12-31 10:42:11 修改

阅读量1.4k

点赞数 20

分类专栏：运动规划与控制文章标签：论文阅读

于 2024-12-18 20:35:32 首次发布

本文链接：https://blog.csdn.net/m0_61750953/article/details/144554405

版权

加州理工学院的研究团队在新一期《Science Robotics》期刊上公布了一项突破性的研究成果——动态系统规划的谱展开蒙特卡罗树搜索。这种名为“谱展开树搜索”（Spectral Expansion Tree Search，简称SETS）的实时规划算法，加强了机器人通过实时计算来规划复杂行为的能力，而不是坚持预先设计或离线学习的例程，减轻了对每个问题实例的专门算法或训练的需求。

文章地址：https://www.science.org/doi/epdf/10.1126/scirobotics.ado1010

github：https://github.com/aerorobotics/sets

概览图：

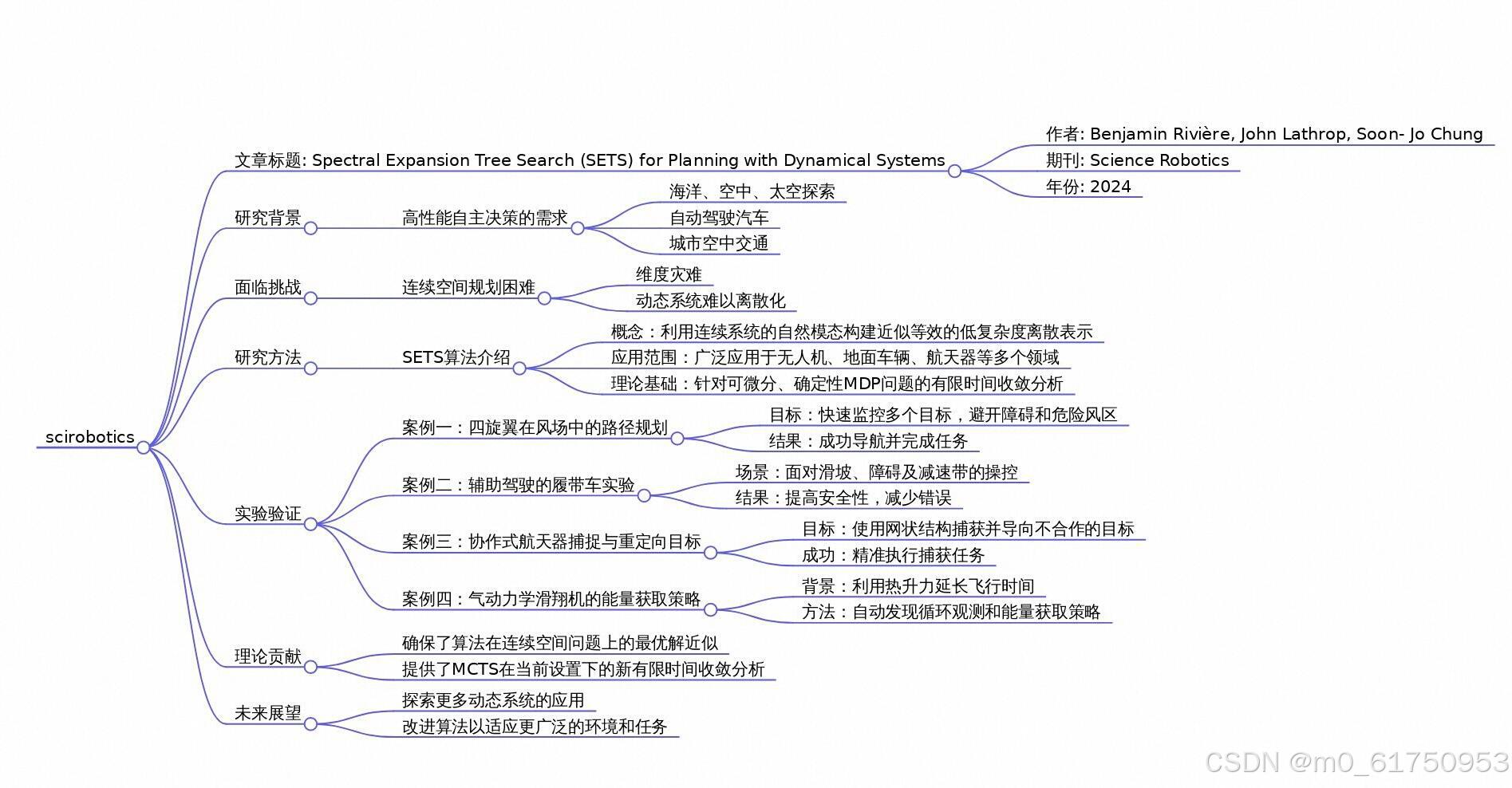
概述

文章介绍了一种新的实时规划算法——谱展宽树搜索（SETS），用于处理具有连续动态系统的决策制定问题。与其他方法相比，SETS通过利用系统局部线性化的谱信息来构造一个低复杂度且近似等效的离散问题表示，从而实现了对连续动态系统的高效规划。该算法被证明对于一类包括非线性动力学、非凸奖励函数和不规则环境在内的确定性和可微分的马尔科夫决策过程（MDP）问题，能够收敛到全局最优解的一个界限。通过一系列实验验证，包括无人机在复杂风场中的路径规划、地面车辆与人类协同驾驶以及空间探测器编队捕获目标等，展示了SETS在解决实际问题上的有效性和普适性。此外，还通过数值实验对比了不同规划策略的有效性，进一步证明了SETS算法的优势。总的来说，SETS提供了一种有效的解决方案，使得机器人能够在高维连续动力学系统中进行实时的最优决策制定，有望推动自主机器人技术的发展并拓展其应用领域。

1. Monte Carlo tree search (MCTS)算法

赋予机器人高性能和可靠的自主决策能力，是机器人研究领域的重要目标，这将为如海洋、空中和空间的自主探索、自动驾驶汽车以及城市空中交通等应用铺平道路。这些自主系统不仅需要处理低级别的物理运动规划，还需进行高级别的策略决策，比如目标选择、动作排序和其他决策变量的优化。

不过想要实现机器人高性能的自主决策能力非常困难，尤其是在高维连续空间中精确解决决策问题时会面对“维度诅咒”的问题。

       “维度诅咒”（Curse of Dimensionality）是数学、计算机科学和信息理论中的一个概念，它描述了在处理高维数据时遇到的一系列问题。随着空间维度的增加，数据点之间的距离特性发生显著变化，导致许多传统的算法和技术变得低效或不适用。具体来说，“维度诅咒”的问题包括但不限于以下几点：

        稀疏性：在高维空间中，即使数据集非常大，数据点也会变得极其稀疏。这意味着，对于任何给定的数据点，很难找到“近邻”，因为大多数其他点都相距甚远。这种稀疏性使得基于距离度量的算法（如聚类、分类等）的效果大打折扣。

        指数增长的计算复杂度：当维度增加时，搜索空间的大小呈指数级增长。例如，在离散化空间进行搜索时，如果每个维度有n个可能的值，那么d维空间将有n^d个组合。这使得遍历整个搜索空间变得计算上不可行。

        样本需求的增加：为了维持模型的准确性，通常需要随维度线性或甚至更快地增加训练样本的数量。在高维情况下，获取足够多的代表性样本可能是不切实际的。

        特征选择与降维的重要性：由于并非所有维度都是相关或有用的，因此在高维数据中识别出真正有助于分析的特征变得至关重要。这也促使了诸如主成分分析（PCA）、t-SNE等降维技术的发展。

        距离函数失效：随着维度的增加，不同点之间的欧几里得距离趋于相同，从而降低了距离作为相似性度量的有效性。这对依赖于距离测量的算法（如k-最近邻算法）构成了挑战。

        优化困难：在高维空间中寻找全局最优解变得更加困难，因为局部极值的数量可能会急剧增加，使得梯度下降等优化方法容易陷入次优解。

为了在部署中提高计算效率，许多现有的方案通过利用特定问题结构来简化问题，而不是直接面对一般化的难题。

例如，在运动规划中通过采样方法来实现，轨迹优化可以依赖凸优化技术，而高层离散决策则可以通过值迭代算法来解决。这些方法也可以分层组合，以应对更为复杂的行为模式，如多航天器轨道检查、机器人操作任务和城市环境中的自动驾驶车辆。虽然这种方法能够提高了计算效率、但它们的应用范围有限，难以适应新问题，对设计者提出了不断增长的要求。此外，有些问题不能简单地分解成计算上可处理的小问题。

强化学习是一种替代方案，它使用历史数据（即轨迹）来训练能够做出最优决策的策略。与传统方法不同，强化学习泛化性更强，适用于更广泛的问题类别。这种灵活性使得无人机竞速、直升机飞行、抓取任务和双足行走等领域取得了重要进展。不过，这些方法通常需要一个离线训练阶段，限制了它们在新或动态环境中的适用性。并且由于其黑箱性质，强化学习方法难以解释，并且在最优性、稳定性和鲁棒性方面提供的保证有限。

一些基于规划和模型的强化学习方法使用基于树的算法，这些算法使用一系列统称为蒙特卡罗树搜索(MCTS)的方法。与离线学习方法相比，MCTS从当前状态出发，战略性地探索模拟的未来路径，实时生成高质量的解决方案。通过给定系统的动态特性和奖励函数，MCTS在限定的计算预算内返回最佳可能计划。MCTS在离散空间中表现良好，但在机器人的连续空间中，统一的空间和时间离散化会导致非常大的搜索树和缓慢的收敛速度，从而MCTS对连续问题的表示效果不佳。

关于蒙特卡罗树搜索的原理可以参考：