读《GMC: Graph-based Multi-view Clustering》

摘要

基于多视图的聚类旨在为多视图数据提供聚类解决方案。然而，大多数现有的方法都没有充分考虑不同视图的权重，而需要一个额外的聚类步骤来生成最终的聚类，甚至还得基于所有视图的固定图相似度矩阵来优化其目标。
本文提出了一个通用的基于图的多视图聚类(GMC)来解决这些问题。GMC获取所有视图的数据图矩阵，并将它们融合起来生成一个统一的图矩阵。统一的图矩阵进而改进了每个视图的数据图矩阵，并直接给出了最终的聚类。

一种新的多视图融合技术可以自动加权每个数据图矩阵，（有点类似于求和式的特征层融合？）得到统一的图矩阵。对统一矩阵的图拉普拉斯矩阵也施加了一个不引入调整参数的秩约束，这有助于将数据点自然划分为所需的簇数。提出了一种优化目标函数的交替迭代优化算法。

1.引言

多视图学习[1]，[2]

本文重点关注多视图无监督学习，特别是多视图聚类。与单视图聚类[3]，[4]相比，多视图聚类探索和利用来自多视图的互补信息来产生更准确和更健壮的数据分区。

在多视图聚类方法中，有代表性的是基于图的方法[5]、[6]、[7]、[8]、[9]、[10]、[11]、[12]。

聚类结果通常用于后续的应用程序，如社区检测、推荐和信息检索。

基于多视图的聚类方法通常首先在所有视图的输入图中找到一个融合图，然后在这个融合图上使用一个额外的聚类算法来生成最终的聚类（靠，这有点组内想法的意思，就是把单一对象的所有视图融成一个融合图，通过聚类等手段划分视图内和视图间的节点关系，这样才得到一个对象的图，然后再拿这些图用到后面的聚类等任务？）。
虽然这些方法已经取得了最先进的性能，但它们仍然有一些局限性。
首先，如[5]，没有考虑不同视图的重要性差异（没有区分模态间关系吗？），于是本文通过自动生成的权重来处理差异。
其次，许多现有的方法都需要一个额外的聚类步骤来在融合后生成最终的聚类，例如，[5]、[6]、[7]，而本文直接产生融合中的聚类，而没有额外的聚类步骤。
第三，目前大多数方法都孤立地构建每个视图的图（又是决策层融合？），并在融合过程中保持构建图的固定（？），如[5]、[6]、[7]、[9]、[10]、[12]，而本文共同构造了每个视图图和融合图（？），这俩可以很自然地相互帮助。

为啥要纠结这仨问题？ 首先，样本选择偏差导致视图多样性[13]。 其次，额外的聚类步骤会带来额外的PAC（Probably
Approximately Correct可能正确的）边界[14]。 第三，不同的相似度度量对多视图聚类质量有影响[15]。

本文提出了一种新的多视图聚类模型，用基于图的多视图聚类(GMC)表示。
GMC不仅可以自动加权每个视图，并在融合后直接生成最终的聚类，而无需执行任何额外的聚类步骤，而且还可以共同构建每个视图的图和融合图，使它们能够以相互强化的方式相互帮助（恁牛嘞）。
首先，每个视图的数据矩阵首先被转换为由相似性图矩阵生成的图矩阵，记作相似性诱导图(SIG)矩阵。
然后将所提出的融合方法应用于所有视图的SIG矩阵，以便从SIG矩阵中学习一个统一的矩阵（即融合图矩阵）U。U的学习会自动考虑不同视图(v)的不同权重$(w_v)$。
同时，利用学习到的统一矩阵U，再对每个视图的SIG矩阵进行改进。对统一矩阵的拉普拉斯矩阵LU进行秩约束，以约束统一矩阵中连通分量的数量等于所需的簇数c。因此，GMC对每个视图的SIG矩阵进行了加权和改进，并同时生成统一的矩阵和最终的簇。

2.相关

基于图的多视图聚类[5]、[6]、[7]、[8]、[9]、[10]、[11]、[12]
[5]中提出了一种基于3阶段图的多视图聚类方法，它利用子空间的图表示和层次凝聚聚类方法，可惜没考虑不同视图的权重。
于是又有[6]，[7]研究了基于加权图的多视图聚类，首先为每个视图生成一个图，然后对每个图进行权重，通过K-means构建一个统一表示以生成最终簇。
[8]、[9]、[10]、[11]、[12]提出了更先进的加权方法。
可是虽然这些方法在不需要其他聚类算法的情况下生成最终的聚类，但它们却是单独构建每个视图的图（万恶之源决策层），并在融合过程中保持所构建的图不变，除了学习所有视图的全局图而不是每个视图一个图的[8]和[11]
除了上述方法使用的成对相似矩阵融合外，[16]，[17]还提出了交叉图随机游走的高阶相似矩阵（即数据簇相似矩阵）融合，其中数据簇相似性是数据点与聚类中心之间的相似性。虽然可以避免成对相似度矩阵中的高计算复杂度，但它们需要运行一个额外的聚类算法。

多视图谱聚类[18]、[19]、[20]、[21]、[22]、[23]、[24]、[25]
谱聚类以数据点为节点，根据相似性造边[21]，也就是说谱聚类的输入是一个相似性图。
与基于图的聚类的不同之处在于，谱聚类通常首先找到数据的低维嵌入表示，然后对这种嵌入表示执行K-means来生成最终的聚类。不过多视图谱聚类还需要在嵌入表示上进行额外的聚类步骤。
基于图的聚类在构建的数据图上生成聚类，而不是新的嵌入表示

除了基于多视图图的聚类和多视图谱聚类外，还有一些其他的多视图聚类方法
大致可分为三类：协同训练式的聚类[19]，[26]，[27]，[28]，多核聚类[29]，[30]，[31]，[32]，和多视图子空间聚类[33]，[34]，[35]，[36]，[37]，[38]，[39]，[40]，[41]，[42]，[43]。
协同训练式的聚类使用协同训练策略[44]，通过先验知识或学习到的知识来引导不同视图的分区，迭代执行这一策略，所有视图的分区将得到最广泛的共识。
多核聚类预定义了一组基核，然后以线性或非线性的方式组合这些内核，以提高聚类性能（听起来有点初级啊）
多视图子空间聚类旨在通过假设所有视图共享这个统一表示，从所有视图的特征子空间中学习统一表示。然后，将这个统一的表示输入到一个聚类模型中，得到最终的结果。
协同训练的方法依赖于条件独立性，多核聚类方法计算复杂度高，多视图子空间聚类方法对初始化很敏感。

另外还有[45]、[46]、[47]、[48]、[49]、[50]研究了一些其他多视图学习方法和应用

3.基于图的多视图聚类

3.1 SIG矩阵构建

将相似性矩阵转换为图最常用的方法是使用k-最近邻图。如果xj属于xi的k-最近邻，那么它们就是连接的。边的权重通常由高斯核定义。缺点是，由于数据中的噪声和异常值，难以设置超参数σ。

[51]的研究发现，稀疏表示对噪声和异常值具有鲁棒性。构造一个视图的SIG矩阵，使两个数据点之间的小距离对应大相似值，两个数据点之间的大距离对应小（或零）相似值。为此，本文使用一种稀疏表示方法来构造SIG矩阵。

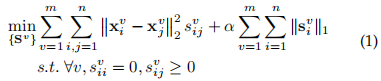
通过归一化惩罚，再增添先验约束

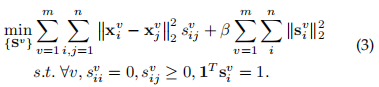
为每个视图独立地构建每个SIG矩阵，因为每个SIG与其他视图没有关系。接下来再将每个SIG矩阵与一个统一的图矩阵耦合

3.2多数据图融合

（有点像矩阵补全的重构损失啊）
通过定理1保证权重w={w1，…wm}是自动确定的。

定理1。如果权值w固定，上面的优化问题等价于

对每个SIG矩阵S1、…，Sm和统一图矩阵U的学习被耦合成一个联合问题。这样，两者的学习就可以自然地互助。

3.3具有约束拉普拉斯秩的多视图聚类

接下来要解决直接在统一图矩阵U上生成聚类结果，而不需要额外的聚类算法或步骤这样的问题。对统一矩阵U的图拉普拉斯矩阵施加秩约束。
在图论中，$L_U=D_U-(U^T+U)/2$被称为图拉普拉斯矩阵(原本拉式矩阵应该是L=D-A，这里应该是通过U和A的关系推导出来的)，其中度矩阵DU是对角阵，第i个对角元素是${\sum }_j(u_{ij}+u_{ji})/2$。如果统一矩阵U是非负的，那么拉普拉斯矩阵有以下定理[53]，[54]。

定理2。拉普拉斯矩阵LU的特征值O的多重性r等于统一矩阵U的图中连通分量的个数。(?)

因此如果rank(LU)=n−c，c=r，则对应的U是将数据点直接划分为c簇的理想情况。
因此，不需要在统一矩阵U上做额外的聚类算法来生成最终的聚类。
于是增加了一个秩约束得到

但是因为LU依赖于目标变量U，而约束rank(LU)=n−c也是非线性的，这就很难办。
记ϑi(LU)为LU的第i小特征值。如果ϑi(LU)≥0则LU半正定[53]。然后，如果${\sum }_{i=1}^c{\vartheta }_i(L_U)=0$，则可以获得约束rank(LU)=n−c。根据定理[55]，有

其中F是嵌入矩阵，是谱聚类的学习对象。于是有

当λ足够大时，最优解会保证${\sum }_{i=1}^c{\vartheta }_i(L_U)=0$。

4.优化

4.1

因为目标函数中的所有变量都是耦合的，所以很难求解（？）。此外，约束条件也不平滑。
参考拉格朗日乘子法，构造出一个交替迭代算法来求解（这里说的拉格朗日乘子法应该是优化目标转成损失函数吧，要不然都可以直接求导出结果了还优化啥？）
总之转化成等价问题

4.2 求解

再整理一下得到损失函数

4.3 分析复杂度

4.4 分析收敛性