SVM:硬/最大间隔SVM（手撕原理）

最新推荐文章于 2022-07-19 21:50:57 发布

褚骏逸

最新推荐文章于 2022-07-19 21:50:57 发布

阅读量375

点赞数 3

分类专栏： machine_learning 文章标签：机器学习 svm 支持向量机算法

本文链接：https://blog.csdn.net/weixin_41171061/article/details/106003828

版权

machine_learning 专栏收录该内容

29 篇文章 3 订阅

订阅专栏

示意图

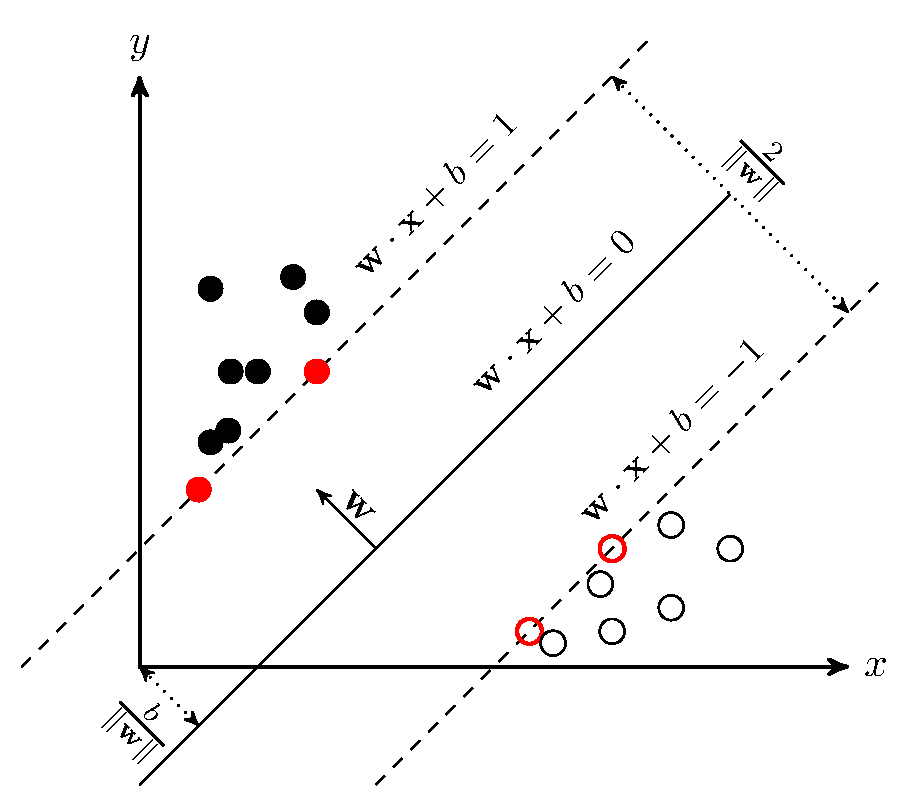
摘自其他人的CSDN博客，未知博客名

二分类问题描述

$Data=\{(x_i, y_i)\}_{i=1}^N,x_i\in\R^p,y_i\in\{-1,+1\}$
由于超平面 $\omega^Tx+b$ 有很多个，要找到最好的一个超平面，以得到最低的泛化误差（或测试误差、期望损失）。

hard-margin SVM判别模型，与概率无关：
$f(\omega)=sign(\omega^Tx+b)=\begin{cases}\omega^Tx+b>0,f(\omega)=1\\\omega^Tx+b<0,f(\omega)=-1\end{cases}$
目标函数：
$\begin{cases}max\space margin(\omega,b) \\ s.t.\space \begin{cases}\omega^Tx_i+b>0,y_i=1\\\omega^Tx_i+b<0,y_i=-1\end{cases}\Rightarrow y_i(\omega^Tx_i+b)>0,i=1...,N\end{cases}$
即， $\begin{cases}max\space margin(\omega,b) \\ s.t.\space y_i(\omega^Tx_i+b)>0,i=1,...,N\end{cases}$

什么是margin？
答：一共有N个点到直线的距离，最小的那个就是margin。点到直线距离公式，
$margin(\omega,b)={min \atop \omega,b,x_i}distance(\omega,b,x_i)={min \atop \omega,b,x_i}{\frac 1 {\parallel\omega\parallel}}\mid\omega^Tx_i+b\mid$

则上式写为：
$\begin{cases}{max \atop \omega,b}{min \atop \omega,b,x_i}{\frac 1 {\parallel\omega\parallel}}\mid\omega^Tx_i+b\mid\space ={max \atop \omega,b}{min \atop x_i}{\frac 1 {\parallel\omega\parallel}}\mid\omega^Tx_i+b\mid={max \atop \omega,b}{\frac 1 {\parallel\omega\parallel}}{min \atop x_i}y_i(\omega^Tx_i+b)\Larr y_i\in\{-1,+1\} \\ s.t.\space y_i(\omega^Tx_i+b)>0\end{cases}$

$y_i(\omega^Tx_i+b)>0$ 可以理解为： $\exist\space\gamma>0,s.t.\space {min \atop x_i,y_i}y_i(\omega^Tx_i+b)=\gamma$
$\gamma$ 的取值对式子（或超平面）是没有影响的，实际上就是对 $\omega,b$ 的缩放。
因此，令 $\gamma=1$ 。
则， $\atop \omega,b}{\frac 1 {\parallel\omega\parallel}}{min \atop x_i}y_i(\omega^Tx_i+b)={max \atop \omega,b}{\frac 1 {\parallel\omega\parallel}}\gamma={max \atop \omega,b}{\frac 1 {\parallel\omega\parallel}}$
则，上式可写为：
$\begin{cases}{max \atop \omega,b}{\frac 1 {\parallel\omega\parallel}}\Rarr{min \atop \omega,b}{\parallel\omega\parallel}={min \atop \omega,b}{\frac 1 2}\omega^T\omega\space硬间隔；二次的、凸优化，可直接求解 \\s.t.\space {min\atop x_i}y_i(\omega^Tx_i+b)=1\Rarr y_i(\omega^Tx_i+b)\geqslant1,i=1,...,N\space 有N个约束 \end{cases}$

则， $(1)\begin{cases}{min \atop \omega,b}{\frac 1 2}\omega^T\omega\space \\s.t.\space y_i(\omega^Tx_i+b)\geqslant1,i=1,...,N \end{cases}$

开始求解

1. Primal problem：带 $\omega,b$ 约束的优化

$(1)\begin{cases} {min \atop \omega,b}{\frac 1 2}\omega^T\omega \\ s.t. \space y_i(\omega^Tx_i+b)\geqslant1,for \space i=1,...,N \xLeftrightarrow{}1-y_i(\omega^Tx_i+b)\leqslant0\end{cases}$

2. 拉格朗日乘子法→对 $\omega,b$ 无约束的优化

$L(\omega,b,\lambda)={\frac 1 2}{\omega^T}\omega+\displaystyle\sum_{i=1}^N\lambda_i(1-y_i(\omega^Tx_i+b))$ , $\lambda_i\geqslant0$
$(2)\begin{cases}{min \atop \omega,b} {max \atop \lambda}L(\omega,b,\lambda) \\ s.t.\space\lambda_i\geqslant0\end{cases}$

值得注意的是： $1-y_i(\omega^Tx_i+b)\leqslant0$ 。为什么呢？
答：
直观上看，
如果 $1-y_i(\omega^Tx_i+b)>0$ ,则 ${max\atop\lambda}L={\frac 1 2}{\omega^T}\omega+\infty=\infty$
如果 $1-y_i(\omega^Tx_i+b)\leqslant0$ ,则 ${max\atop\lambda}L$ 一定存在， ${max\atop\lambda}L={\frac 1 2}{\omega^T}\omega+0={\frac 1 2}{\omega^T}\omega\space(\lambda_i\rarr0)$
则， $\atop \omega,b} {max \atop \lambda}L(\omega,b,\lambda)={min \atop \omega,b} (\infty,{\frac 1 2}{\omega^T}\omega)={\frac 1 2}{\omega^T}\omega$
因此， $1-y_i(\omega^Tx_i+b)>0$ 被丢弃了。

3. 转化为强对偶问题

$(3)\begin{cases}{max \atop \lambda}{min \atop \omega,b}L(\omega,b,\lambda) \\s.t.\space \lambda_i \geqslant0\end{cases}$

什么是强、弱对偶？
答：凸优化二次规划问题，它的约束是线性的，目标函数是二次的，因此满足强对偶关系。（可证）
（1）弱对偶关系为 $min\space maxL\geqslant max\space minL$ ，对应理解为“尾凤 $\geqslant$ 头鸡”，即凤尾优于鸡头、瘦死的骆驼比马大。
（2）强对偶关系，就是把 $\geqslant$ 改为=。

4. 求解对偶问题：解拉格朗日方程 $\atop \omega,b}L(\omega,b,\lambda)$

$L(\omega,b,\lambda)={\frac 1 2}{\omega^T}\omega+\displaystyle\sum_{i=1}^N\lambda_i(1-y_i(\omega^Tx_i+b))$ , $\lambda_i\geqslant0$

(1) 求 ${\frac {\partial L} {\partial b}}=0$

${\frac {\partial L} {\partial b}}={\frac {\partial }{\partial b}}[\displaystyle\sum_{i=1}^N\lambda_i-\displaystyle\sum_{i=1}^N\lambda_iy_i(\omega^Tx_i+b)]={\frac {\partial }{\partial b}}[-\displaystyle\sum_{i=1}^N\lambda_iy_ib)]\\=-\displaystyle\sum_{i=1}^N\lambda_iy_i=0$
则， $\displaystyle\sum_{i=1}^N\lambda_iy_i=0$

(2) 将 $\displaystyle\sum_{i=1}^N\lambda_iy_i=0$ 代入到 $L(\omega,b,\lambda)$ 中

$L(\omega,b,\lambda)={\frac 1 2}\omega^T\omega+\displaystyle\sum_{i=1}^N\lambda_i-\displaystyle\sum_{i=1}^N\lambda_iy_i(\omega^Tx_i+b)\\={\frac 1 2}\omega^T\omega+\displaystyle\sum_{i=1}^N\lambda_i-\displaystyle\sum_{i=1}^N\lambda_iy_i\omega^Tx_i+\displaystyle\sum_{i=1}^N\lambda_iy_ib\\={\frac 1 2}\omega^T\omega+\displaystyle\sum_{i=1}^N\lambda_i-\displaystyle\sum_{i=1}^N\lambda_iy_i\omega^Tx_i$

(3) 求 ${\frac {\partial L} {\partial \omega}}=0$

${\frac {\partial L} {\partial \omega}}={\frac 1 2}·2·\omega-\displaystyle\sum_{i=1}^N\lambda_iy_ix_i=0$
则， $\omega=\displaystyle\sum_{i=1}^N\lambda_iy_ix_i$

(4) 将 $\omega=\displaystyle\sum_{i=1}^N\lambda_iy_ix_i$ 代入到 $L(\omega,b,\lambda)$ 中

$L(\omega,b,\lambda)={\frac 1 2}(\displaystyle\sum_{i=1}^N\lambda_iy_ix_i)^T(\displaystyle\sum_{i=1}^N\lambda_iy_ix_i)+\displaystyle\sum_{i=1}^N\lambda_i-\displaystyle\sum_{i=1}^N\lambda_iy_i(\displaystyle\sum_{j=1}^N\lambda_jy_jx_j)^Tx_i$

注意：
∵ $\lambda_i\in\Reals,y_i\in\{-1,1\},x_i\in\Reals^p$
∴( $\displaystyle\sum_{i=1}^N\lambda_iy_ix_i)^T=\displaystyle\sum_{i=1}^N\lambda_iy_ix_i^T$
∴ $\omega^T\omega=(\displaystyle\sum_{i}^N\lambda_iy_ix_i^T)·(\displaystyle\sum_{j}^N\lambda_jy_jx_j)=\displaystyle\sum_{i}^N\displaystyle\sum_{j}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j$
同理， $\displaystyle\sum_{i=1}^N\lambda_iy_i(\displaystyle\sum_{j=1}^N\lambda_jy_jx_j)^Tx_i=\displaystyle\sum_{i=1}^N\lambda_iy_i\displaystyle\sum_{j=1}^N\lambda_jy_jx_j^Tx_i\\=\displaystyle\sum_{i}^N\displaystyle\sum_{j}^N\lambda_i\lambda_jy_iy_jx_j^Tx_i\\=\displaystyle\sum_{i}^N\displaystyle\sum_{j}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j\Larr x_i^Tx_j=x_j^Tx_i\in\Reals$
发现上面两个结果一样！因此，可以约掉啦~
$(\displaystyle\sum_{i=1}^N\lambda_iy_ix_i)^T(\displaystyle\sum_{i=1}^N\lambda_iy_ix_i)=\displaystyle\sum_{i=1}^N\lambda_iy_i(\displaystyle\sum_{j=1}^N\lambda_jy_jx_j)^Tx_i\\=\displaystyle\sum_{i}^N\displaystyle\sum_{j}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j$

$L(\omega,b,\lambda)=\displaystyle\sum_{i=1}^N\lambda_i-{\frac 1 2}\displaystyle\sum_{i}^N\displaystyle\sum_{j}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j\xRightarrow{即} {min \atop \omega,b}L(\omega,b,\lambda)$
代入式（3）即，
$(4)\begin{cases}{max \atop \lambda}\displaystyle\sum_{i=1}^N\lambda_i-{\frac 1 2}\displaystyle\sum_{i=1}^N\displaystyle\sum_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j\Larr {max \atop \lambda}{min \atop \omega,b}L(\omega,b,\lambda) \\s.t.\space \lambda_i\geqslant0,\displaystyle\sum_{i=1}^N\lambda_iy_i=0 \end{cases}$

(5) 对偶问题的最终优化式

最优化问题常由 $m i n$ 表示
$(5)\begin{cases}{min \atop \lambda}{\frac 1 2}\displaystyle\sum_{i=1}^N\displaystyle\sum_{j=1}^N\lambda_i\lambda_jy_iy_jx_i^Tx_j-\displaystyle\sum_{i=1}^N\lambda_i \\s.t.\space \lambda_i\geqslant0,\displaystyle\sum_{i=1}^N\lambda_iy_i=0 \end{cases}$

5. KKT条件求解对偶问题

定理：原问题和对偶问题具有强对偶关系 $\xLeftrightarrow{充要条件}$ 满足KKT条件

拉格朗日方程（上面第2点）：
$L(\omega,b,\lambda)={\frac 1 2}{\omega^T}\omega+\displaystyle\sum_{i=1}^N\lambda_i(1-y_i(\omega^Tx_i+b))$ , $\lambda_i\geqslant0$

根据定理可直接得到该问题的KKT（Karush-Kuhn-Tucker）条件：
$\begin{cases}{\frac {\partial L}{\partial \omega}}=0,{\frac {\partial L}{\partial b}}=0,{\frac {\partial L}{\partial \lambda}}=0 \\\lambda_i\geqslant0\Rarr 拉格朗日乘子法的要求 \\1-y_i(\omega^Tx_i+b)\leqslant0\Rarr 上面第2点解释了 \\\lambda_i(1-y_i(\omega^Tx_i+b))=0\Rarr此时，L(\omega,b,\lambda)={\frac 1 2}\omega^T\omega，为最大值；松弛互补条件，求解b^* \end{cases}$
根据KKT条件，可求出最优的 $\omega^*,b^*$ 。
凸优化中对偶问题详解，尤其解释了什么是KKT条件。

(1) 最优解 $\omega^*=\displaystyle\sum_{i=1}^N\lambda_iy_ix_i$

就是之前（3）中 ${\frac {\partial L} {\partial \omega}}=0$ 的结果。

(2) 最优解 $b^*=y_k-\displaystyle\sum_i^N\lambda_iy_ix_i^Tx_k$

假设 $\exist (x_k,y_k),\space s.t.\space 1-y_k(\omega^Tx_k+b)=0$ ,即 $x_k,y_k)$ 为支持向量， $\omega^Tx_k+b\in\{-1,1\}$ 。
$由y_k(\omega^Tx_k+b)=1 \\∵y_k=±1,y_k^2=1 \\∴y_k^2(\omega^Tx_k+b)=y_k \\∴\omega^Tx_k+b=y_k \\∴b^*=y_k-\omega^Tx_k=y_k-(\omega^*)^Tx_k=y_k-\displaystyle\sum_{i=1}^N\lambda_iy_ix_i^Tx_k$

(3) 根据 $w^,b^$ 得出超平面 $w^x+b^$

$f(x)=sign((w^*)^Tx+b^*)$
$w^*=\displaystyle\sum_{i=1}^N\lambda_iy_ix_i$ 可看做是 $Data=\{(x_i, y_i)\}_{i=1}^N,x_i\in\R^p,y_i\in\{-1,+1\}$ 的线性组合
$\lambda_i$ 只对支持向量才有意义，即 $1-y_i(\omega^Tx_i+b)=0$ 上的点，此时， $\lambda_i\geqslant0$ ；对于非支持向量不起作用，此时 $\lambda_i=0$ 。

褚骏逸

关注

3
点赞
踩
1

收藏

觉得还不错? 一键收藏
1
评论
SVM:硬/最大间隔SVM（手撕原理）

示意图二分类问题描述Data={(xi,yi)}i=1N,xi∈Rp,yi∈{−1,+1}Data=\{(x_i, y_i)\}_{i=1}^N,x_i\in\R^p,y_i\in\{-1,+1\}Data={(xi,yi)}i=1N,xi∈Rp,yi∈{−1,+1}由于超平面ωTx+b\omega^Tx+bωTx+b有很多个，要找到最好的一个超平面，以得到最低的泛化误差（或测试误差、期望损失）。hard-margin SVM判别模型，与概率无关：f(ω)=sign(ωTx+b)={ω
复制链接

扫一扫