定义:机器学习算法在学习过程中对某种类型假设的偏好。
每种算法必有其归纳偏好,否则它将被假设空间中看似在训练集上“等效”的假设所迷惑,无法产生确定的学习结果。
例子理解:
| 编号 | 色泽 | 根蒂 | 敲声 | 好瓜 |
| 1 | 青绿 | 蜷缩 | 浊响 | 是 |
| 2 | 乌黑 | 蜷缩 | 浊响 | 是 |
| 3 | 青绿 | 硬挺 | 清脆 | 否 |
| 4 | 乌黑 | 稍蜷 | 沉闷 | 否 |
西瓜的好坏到底取决于三种特征的哪一种或几种,根据编号1和2可以假设的影响因素为:
1.根蒂+敲声
2.根蒂
3.敲声
如果没有归纳偏好,择无法确定具体的影响好瓜的特征,如果一个测试用例为乌黑、蜷缩、清脆则不确定采取以上三种那种方式进行判断:可能用1判断为坏瓜,可能用2判断为好瓜,可能用3判断为坏瓜
假设归纳偏好为2,则直接判断该瓜(乌黑、蜷缩、清脆)为好瓜。
奥卡姆剃刀(归纳偏好原理):
若有多个假设与观察一致,则选择最简单的那个。哪个才是最简单的呢,这就需要对应不同的算法,所以引出了问题,哪种算法才是最好的呢?
NFL(没有免费的午餐)原则:
假设的误差与学习算法无关!学习算法没有好坏之分,不能脱离具体问题,要根据实际问题选取相应的学习算法
证明过程:
(3) 式:由于假设“真实目标函数对所有可能的 f 均匀分布”,故对所有 f 求和后,任意假设 h 的准确率期望为一半。又由于 1 在正确时取 1 反之为 0,故(2) 式末尾对 f 的求和得到的值为假设空间个数的一半,即得 (3) 式。
(5) 式:即简单的概率求和,P(h|X,a) 对 h 求和当然就是 1了。还不理解的话?其实就是 P(A|B) 对 A 求和的形式。
可知算法a和算法b的误差是相同的








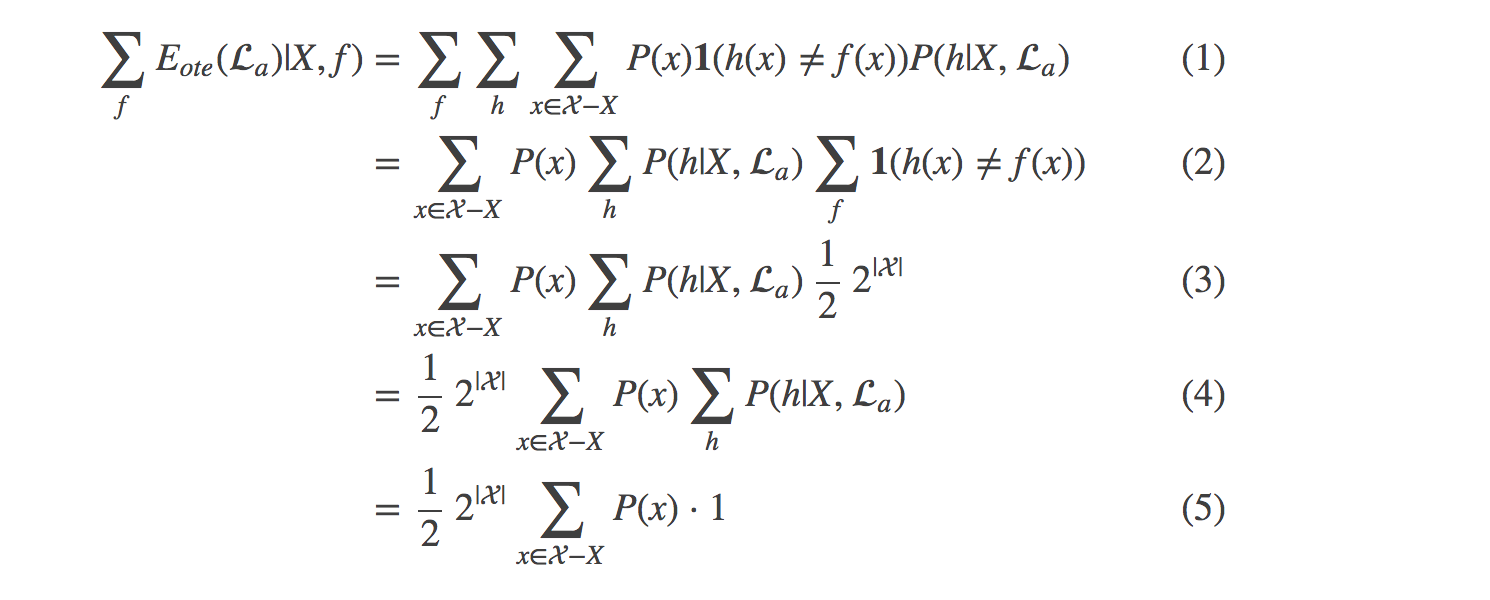
















 4662
4662

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








