【机器学习】感知机算法

1. 思想

感知机的思想是错误驱动，即将分类错的样本数目作为损失函数，目的是使分类错的样本最少，即使损失函数的值最小。

2. 激活函数

假设需要分类的样本为二分类，为了将样本分为两类。我们选取激活函数为：

通过该激活函数，我们可以将线性回归的结果a映射到+1和-1，也就是要分的两个类别。其中，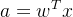

3. 损失函数的选择

3.1 损失函数为不连续函数

3.1.1 公式

3.1.2 公式说明

由激活函数可知，当分类正确时，与同号，此时；当分类错误时，与异号，此时。表示当分类错误时取值为1，分类正确时，取值为0。L(w)则是分类错误的样本的总数据。我们的目标是使该损失函数最小。

3.1.3 缺点

既然明确了目标，就要开始付诸行动了。通常我们如何找到一个函数的最小值呢？那就是求导。但是很明显，这里的损失函数是不可导的，它不是一个连续函数，因此我们需要更换一下函数的表达形式，具体将在3.2说明。

3.2 损失函数为连续函数

3.2.1 公式

 3.1.2 公式说明

由于3.1.1的公式是不可导的，难以求出令损失函数为极小值的w的估计值。因此，这里转换为3.2.1的形式。在这个公式中，我们将损失函数看做是w的连续函数，因为w每一个微小的变化都会引起L(w)的改变。换句话说，每当，损失函数都会发生一定的改变，即 。此时，我们就可以通过求导的方式来找极小值了。

3.1.3 求解方式选取

显然，若将L对w求偏导，我们可以得到

此时无法求解出最佳的w，因此需要改变一下思路，选择随机梯度下降的算法。在我的其他文章中，也有介绍梯度下降，如有不熟悉的读者可以参考。 梯度下降传送门

通过这次求导，其实我们已经找到了损失函数L(w)的梯度。此时只需沿负梯度改变w的取值即可，如下所示：

其中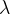， 是步长。随着w的不断迭代，我们最终可以找到一个局部最优解，得到感知机的决策边界。

4 缺点

• 单一感知机无法处理多分类
• 无法处理线性不可分的数据集
• 由于没有找出最佳的决策边界，容易过拟合（SVM是对其的改进）