用赤池信息量准则（AIC）选择最佳模型：小学生也能懂的指南

​​​​​​

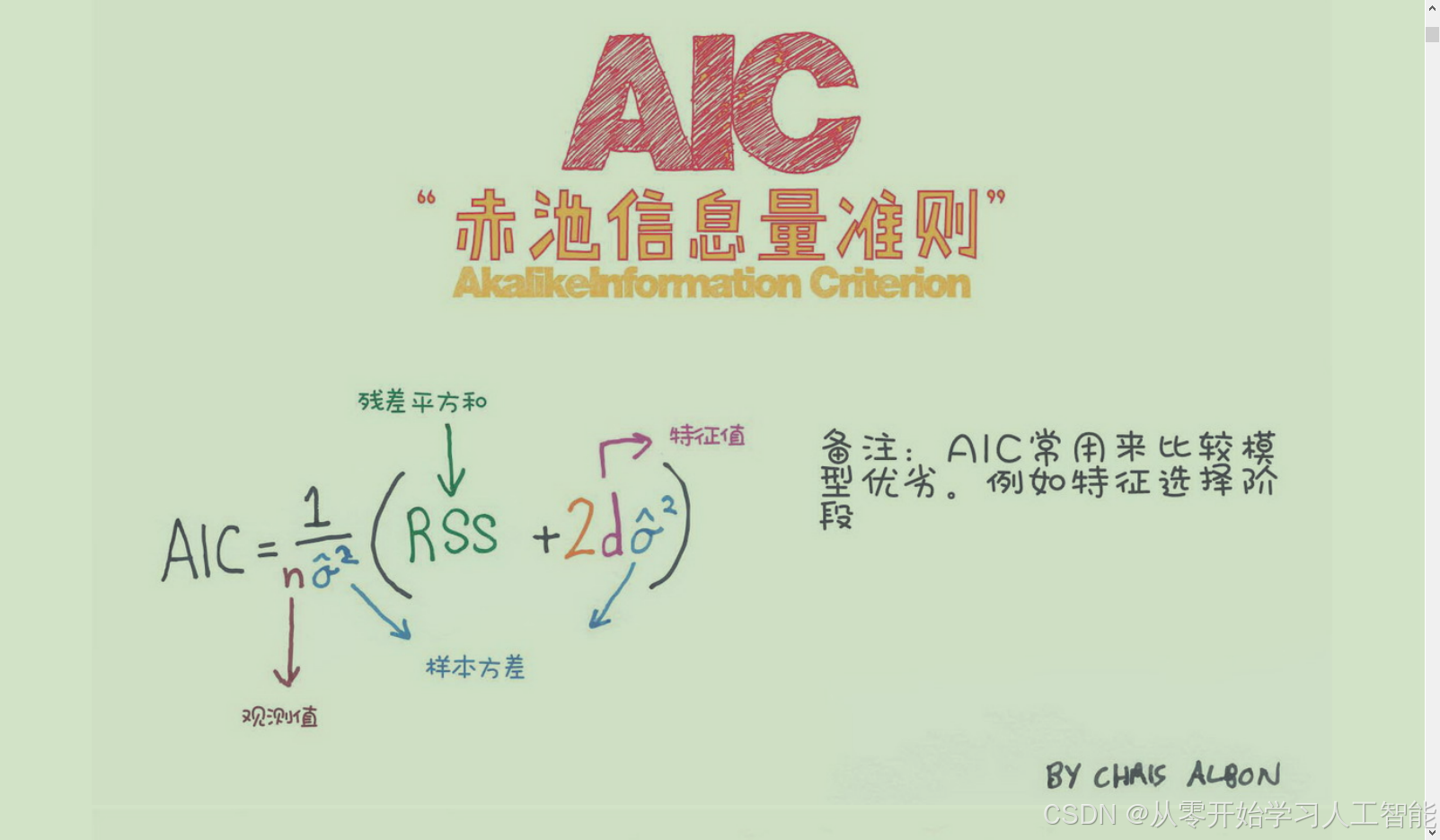
让我们用简单的语言来解释一下赤池信息量准则（Akaike Information Criterion，简称AIC），并包含必要的公式。

什么是AIC？

AIC是一种衡量统计模型相对质量的指标。它帮助我们选择一个模型，这个模型在尽可能准确地拟合数据的同时，保持简洁性。AIC考虑了模型的拟合度（即模型对数据的解释能力）和模型的复杂度（即模型中参数的数量）。

AIC的公式

AIC的公式如下：

$$[AIC=\frac{1}{n{\hat{\sigma }}^2}(RSS+2d{\hat{\sigma }}^2)]$$
其中：

• ( RSS ) 是残差平方和（Residual Sum of Squares），即所有数据点与模型预测值之间差的平方和。

• ( n ) 是观测值的数量。

• ( d ) 是模型中参数的数量（包括截距）。

• $$({\hat{\sigma }}^2)$$

  是样本方差，它是残差平方和除以自由度（( n - d )）的估计值。

简单解释

想象一下，你在用积木搭建一个桥梁模型。AIC就像是在评价你的桥梁模型时，考虑了你用了多少积木以及模型与真实桥梁的相似度。如果用了很多积木但模型并没有变得更好，AIC就会变高，告诉你这个模型可能不是最好的。

为什么使用AIC？

在构建模型时，我们希望模型既准确又简洁。AIC帮助我们理解，增加更多的参数是否真的提高了模型的预测能力，还是只是让模型变得复杂而没有实际的好处。这样，我们就可以构建一个既有效又不会过度复杂的模型。

AIC的计算步骤

1. 计算残差平方和（RSS）：这是模型预测值与实际观测值之间差异的平方和。
2. 估计样本方差$$({\hat{\sigma }}^2)$$：这通常是RSS除以自由度（( n - d )）。
3. 计算AIC：将RSS和参数数量（( d )）代入公式。

举个例子

假设我们有一个模型，它使用房子的大小、房间数量和位置来预测房子的价格。这里，我们有3个自变量加上一个截距，所以 ( d = 4 )。如果我们有100个房子的数据点，那么 ( n = 100 )。我们计算出RSS和
$$({\hat{\sigma }}^2)$$
，然后代入AIC公式，得到AIC的值。