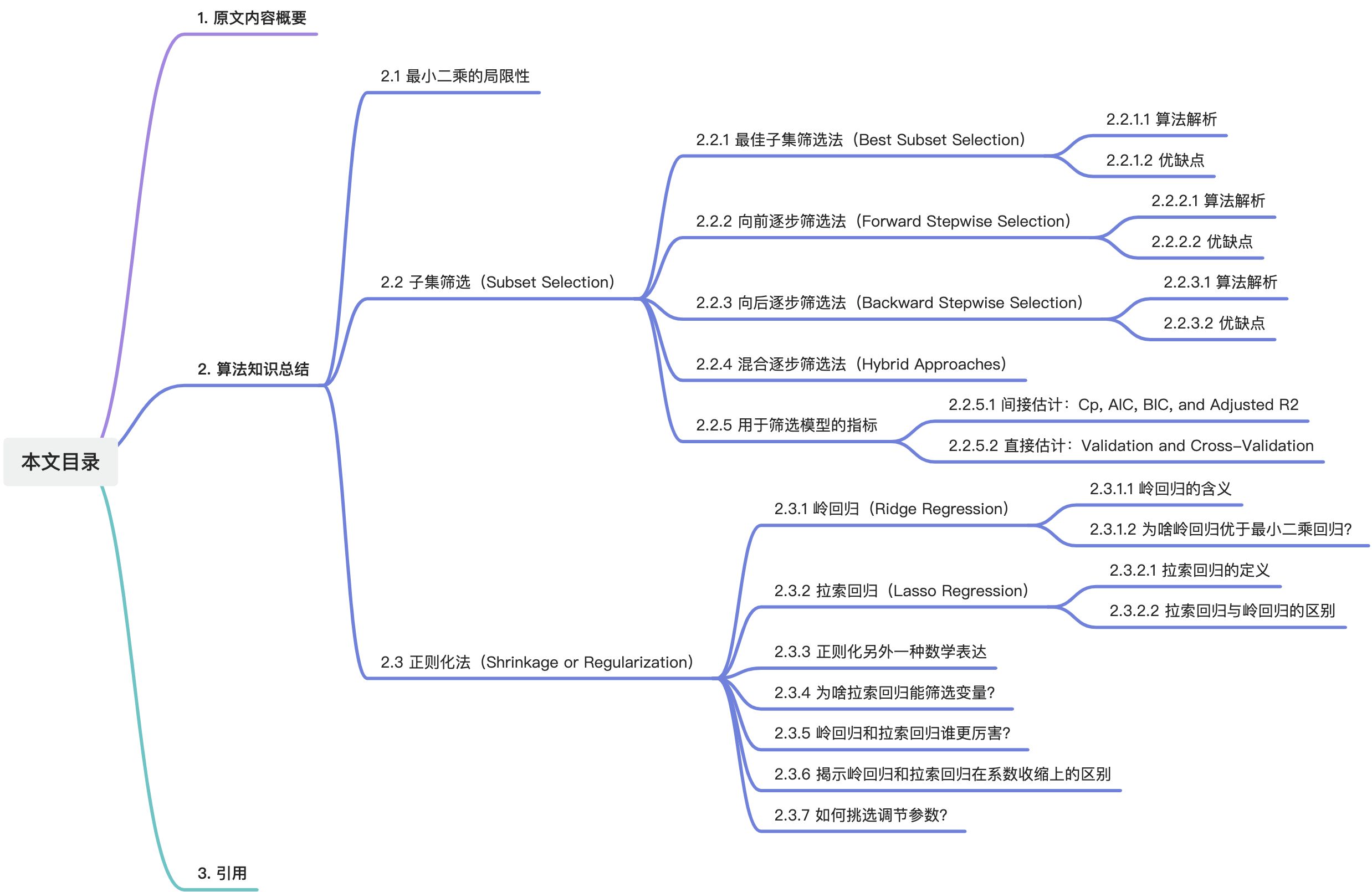
目录
1. 原文内容概要
在数据的宇宙里,构建机器学习模型犹如在夜空中绘制星座,既需精确又求优雅。但这片宇宙并非一望无际的清晰,充满了噪声和冗余的迷雾。为了揭开数据深处的秘密,我们必须进行一场艺术之旅——筛选出有价值的变量(Subset Selection)、用正则化雕塑模型(Shrinkage Methods)、通过降维探寻低维空间的奥秘(Dimension Reduction Methods)。
本篇读书笔记将带你深入这场机器学习中的模型炼金术,揭秘如何在复杂与简洁之间雕刻出平衡,将混沌的数据雕琢成洞察力强、预测精准的模型。
由于内容较多,第六章的读书笔记会分成【上】、【下】两部分输出。【上】部分将介绍“子集筛选”和“正则化”,【下】将介绍“降维”方法。
2. 算法知识总结
2.1 最小二乘的局限性
大家先回忆下线性模型的基本表现形式:
线性模型虽然简单,但现实生活中用处非常广泛。拟合线性模型最基础的方法当属“最小二乘法”,这种方法理解起来特别顺畅,但经常会用不上劲(变量数大于样本数时)和用力过猛(过拟合的情况)。为了提高线性模型的拟合质量,有必要对“最小二乘法”进行一些优化改进。
具体来讲,可以从两个方面来探究最小二乘法的局限性:
1)预测精度方面:如果自变量和因变量之间近似线性相关,并且样本量显著多于变量数,那么使用最小二乘法可以构建一个精确度较高的模型。然而,在样本量与变量数相差不大的情况下,该模型容易发生过拟合现象(However, if n is not much larger than p, then there can be a lot of variability in the least squares fit, resulting in overfitting and consequently poor predictions on future observations not used in model training)。当样本量少于变量数量时,最小二乘法将无法得出唯一解,因此变得无效(And if p > n, then there is no longer a unique least squares coefficient estimate: there are infinitely many solutions)。在这种情况下,存在多个解可以使训练误差降至零,导致极端的过拟合现象。
2)模型解释方面:在使用线性模型时,很多自变量可能与因变量无关。为了剔除这些无关变量(也就是将对应的变量系数变为
0
0
0),降低模型复杂度并提高可解释性,我们需要采用特定的变量选择算法。由于最小二乘法本身不具备变量筛选功能,所以必须借助其他算法来实现这一目的(Now least squares is extremely unlikely to yield any coefficient estimates that are exactly zero)。
由此引出子集筛选、正则化、降维等优化方法。
2.2 子集筛选(Subset Selection)
2.2.1 最佳子集筛选法(Best Subset Selection)
2.2.1.1 算法解析
这种方法采用了一种直接而全面的策略,即尝试每一种可能的组合方式,进而从中筛选出最优解。具体操作步骤可以概括为以下三点,我们以线性回归问题为例来说明:
1)
M
0
M_0
M0是一个初始模型(null model),不含有任何解释性变量。由于缺乏预测因子,该模型的预测策略简化为使用数据集的整体均值作为每个预测点的输出。
2)设定
k
k
k的取值范围为
1
,
2
,
…
p
1,2,…p
1,2,…p,其中
p
p
p表示可用变量的总数,
k
k
k表示在当前循环迭代中,模型所包含的变量数量。对于每个
k
k
k值,遍历所有可能的变量组合,并为每种组合拟合相应的模型(即下图中的步骤a);接着,使用一个评估模型性能的指标(例如残差平方和
R
S
S
RSS
RSS或决定系数
R
2
R^2
R2)来挑选出表现最佳的模型,将其标记为
M
k
M_k
Mk(即下图中的步骤b)。通过这一过程,加上最初得到的初始模型
M
0
M_0
M0,最终得到了
p
+
1
p+1
p+1个候选模型。
3)针对上一步的
p
+
1
p+1
p+1个模型,将它们放在独立的验证集上进行预测,再根据衡量模型精度的指标选出最优秀的那一个。
下文中最佳子集筛选法简称best方法。
2.2.1.2 优缺点
这种方法的优点是易理解,缺点就是难计算。对于
p
p
p个待筛变量来说,我们一共会拟合
2
p
2^p
2p种不同的变量组合。当变量数量超过40个时,即便是性能强大的计算机也会无能为力(Consequently, best subset selection becomes computationally infeasible for values of p greater than around 40, even with extremely fast modern computers)。
另一个不利之处是,随着搜索空间的扩大,模型过拟合的风险也随之增加(The larger the search space, the higher the chance of finding models that look good on the training data, even though they might not have any predictive power on future data. Thus an enormous search space can lead to overfitting and high variance of the coefficient estimates)。
由此引出逐步筛选法。
2.2.2 向前逐步筛选法(Forward Stepwise Selection)
2.2.2.1 算法解析
这个算法理解起来比较绕,分为以下几步,以线性回归问题为例:
1)
M
0
M_0
M0为不含有任何变量的初始模型(null model);
2)首先设定
k
k
k的取值范围为
0
,
1
,
…
,
p
−
1
0, 1, \ldots, p-1
0,1,…,p−1,其中
p
p
p表示可选变量的总数。这里的
k
k
k并不代表模型中的实际变量数,而是表示迭代的轮次。对于每个
k
k
k值,我们执行以下操作:
- 当 k = 0 k=0 k=0时,我们从不含任何额外变量的初始模型 M 0 M_0 M0出发,逐一添加变量(每次增加一个),由于有 p p p个可选变量,我们将得到 p p p个一元模型。根据模型的评价指标(通常使用 R S S RSS RSS或 R 2 R^2 R2),从这 p p p个模型中选出性能最优的一个,这个模型被视为本轮选择的最佳模型,记作 M 1 M_1 M1。
- 当 k = 1 k=1 k=1时,由于上一轮已经选定了一个变量,剩余可选变量数为 p − 1 p-1 p−1。此时在 M 1 M_1 M1的基础上再次逐一添加变量,将产生 p − 1 p-1 p−1个二元模型。利用评价指标从中选出最优模型,并将其标记为 M 2 M_2 M2。
- 依此规律继续操作,每轮结束后已选变量不参与后续选择。直到完成 k = p − 1 k=p-1 k=p−1这一轮次的筛选。
通过上述过程,最终将获得
p
+
1
p+1
p+1个模型,从
M
0
M_0
M0到
M
p
M_p
Mp。
3)针对上一步的
p
+
1
p+1
p+1个模型,将它们放在独立的验证集上进行预测,再根据衡量模型精度的指标选出最优秀的那一个。
下文中向前逐步筛选法简称forward方法。
2.2.2.2 优缺点
在forward方法中,我们共构建了 1 + p ( p + 1 ) 2 \frac{1+p(p+1)}{2} 21+p(p+1)个模型。与best方法所需的 2 p 2^p 2p个模型相比,这显著减少了计算量。例如,当 p = 20 p=20 p=20时,best方法有 2 20 = 1048576 2^{20}=1048576 220=1048576个模型需拟合,而forward方法仅需拟合 1 + 20 × ( 20 + 1 ) / 2 = 211 1+20\times(20+1)/2=211 1+20×(20+1)/2=211个模型。
作者通过在“信贷数据集”上进行实验,比较了模型变量数量从1至4变化时,best方法和forward方法的变量选择结果。观察得出以下结论:
1)尽管forward方法显著减少了计算量,其筛选结果与best方法相比差异不大,这表明forward方法是对best方法的有效替代。
2)forward方法具有一个鲜明的特性,即一旦某个变量在某次迭代中被选入模型,它将在后续的模型中持续出现。以实验中的’rating’变量为例,在best方法下,当模型包含4个变量时,'rating’可能被淘汰;而在forward方法中,它仍会被包含在模型中。鉴于best方法能在固定变量数的前提下保证选出的变量组合是全局最优的,forward方法的结果可视为近似解。因此,forward方法的一个限制在于,它不能保证得到全局最优解。

此外,当变量数量
p
p
p大于样本量
n
n
n时,forward方法依然适用。(Forward stepwise selection can be applied even in the high-dimensional setting where n < p)
2.2.3 向后逐步筛选法(Backward Stepwise Selection)
2.2.3.1 算法解析
后向逐步筛选法(backward elimination)与forward方法在逻辑上相似,但在变量选择的顺序上正好相反。forward方法从不含任何变量的模型开始,并在每一轮迭代中添加一个对模型贡献最大的变量;而backward方法从包含所有变量的模型开始,并在每一轮中移除一个对模型贡献最小的变量。一旦某个变量被移除,它就不会再有机会被重新纳入后续的变量选择过程中。
下文中向后逐步筛选法简称back方法。
2.2.3.2 优缺点
在计算量方面,backward方法也仅需构建 1 + p ( p + 1 ) 2 \frac{1+p(p+1)}{2} 21+p(p+1)个模型,与forward方法相同,同时它也不能保证获得全局最优解。但与forward方法不同的是,当变量数量 p p p大于样本量 n n n时,back方法便不再适用了(Backward selection requires that the number of samples n is larger than the number of variables p, so that the full model can be fit)。
2.2.4 混合逐步筛选法(Hybrid Approaches)
Forward方法擅长引入新变量,而backward方法则能够剔除无效变量,这两种策略互为补充。因此,将这两种方法融合,便形成了所谓的hybrid方法。在变量筛选过程中,这种方法既可以添加有价值的变量,也能够移除当前无用的变量。Hybrid方法在接近best方法的拟合效果的同时,虽然其计算量相较于单纯的forward和backward方法有所增加,但与best方法相比仍旧大幅减少。
(As another alternative, hybrid versions of forward and backward stepwise selection are available, in which variables are added to the model sequentially, in analogy to forward selection. However, after adding each new variable, the method may also remove any variables that no longer provide an improvement in the model fit)
2.2.5 用于筛选模型的指标
众所周知,残差平方和(
R
S
S
RSS
RSS)和决定系数(
R
2
R^2
R2)主要反映的是训练误差,而它们对于测试误差的估计往往存在较大偏差。在模型中随着自变量数目的增加,
R
S
S
RSS
RSS和
R
2
R^2
R2通常会整体上呈现单调递减趋势。因此,这两个指标不适合用于挑选最终的最佳模型。为了获得能更准确估计测试误差的指标,我们通常采取两种方法:
1)我们可以通过调整训练误差来间接估计测试误差,从而修正因模型过度拟合而导致的偏差。
(We can indirectly estimate test error by making an adjustment to the training error to account for the bias due to overfitting)
2)用第五章讲到的验证集法或者交叉验证法对测试误差进行直接估计。
(We can directly estimate the test error, using either a validation set approach or a cross-validation approach)
2.2.5.1 间接估计: C p C_p Cp, AIC, BIC, and Adjusted R 2 R^2 R2
指标一:
C
p
C_p
Cp
其中
d
d
d代表模型中的变量个数,
σ
^
2
\hat{σ}^2
σ^2表示对
ε
ε
ε的估计(一般用包含所有变量的模型进行估计)。可以看到,公式中
2
d
σ
^
2
2d\hat{σ}^2
2dσ^2是一个惩罚项,加入的变量越多,惩罚项的值越大,以此来抵消由于变量增多而引起的
R
S
S
RSS
RSS减少。
指标二:
A
I
C
AIC
AIC
AIC(赤池信息准则)适用于基于最大似然法进行参数估计的模型。在本节的例子中,当误差项符合高斯分布时,最大似然估计与最小二乘估计是等价的。因此,作者在公式中省略了一些常数项,使得AIC的表达式与
C
p
C_p
Cp相同。
指标三:
B
I
C
BIC
BIC
BIC(贝叶斯信息准则)的灵感源自贝叶斯定理,其表达式与AIC相似,主要区别在于惩罚项由
2
d
σ
^
2
2d\hat{σ}^2
2dσ^2变为了
l
o
g
(
n
)
2
d
σ
^
2
log(n)2d\hat{σ}^2
log(n)2dσ^2。由于当样本量
n
>
7
n>7
n>7时,
l
o
g
(
n
)
log(n)
log(n)的值会超过2,BIC对于模型中变量个数的增加施加了更重的惩罚。因此,如果采用BIC作为评价标准,通常会得到一个更为简约的模型,即选择的最优模型包含的变量数量更少。
指标四:The adjusted
R
2
R^2
R2
最大化The adjusted
R
2
R^2
R2(调整后的
R
2
R^2
R2)实际上是在最小化
R
S
S
n
−
d
−
1
\frac{RSS}{n-d-1}
n−d−1RSS。这个公式的含义是,尽管增加模型中的变量数
d
d
d可以使残差平方和(
R
S
S
RSS
RSS)变小,但同时也会导致分母
(
n
−
d
−
1
)
(n-d-1)
(n−d−1)变小。如果加入的是无关的噪音变量,
R
S
S
RSS
RSS减小的幅度将会很有限,而分母减小导致的整体分数增大的幅度会更大,从而使得调整后的
R
2
R^2
R2变大。
C p C_p Cp, A I C AIC AIC, and B I C BIC BIC都有严格的数学证明,但证明过程已超出了这本书的范围,故作者没有提及( C p C_p Cp, AIC, and BIC all have rigorous theoretical justifications that are beyond the scope of this book)。上面提到的公式都是针对使用最小二乘法估计参数的线性模型。然而,即使是对于更复杂的模型,相应的公式背后的基本原理也是相似的。
下面这个图可以看出,用
C
p
C_p
Cp和调整后的
R
2
R^2
R2作为筛选指标,筛选出的最佳模型都是含有6个自变量,而BIC则是4个,符合我们上面提到的“如果采用BIC作为评价标准,通常会得到一个更为简约的模型”的结论。
2.2.5.2 直接估计:Validation and Cross-Validation
验证集法和交叉验证法的详细介绍可以在第五章的学习笔记中找到,此处不再重复。与间接估计相比,直接估计法的优势在于它不需要额外的假设,也无需预先估计参数(例如在计算 C p C_p Cp、AIC和BIC时需要先预估 σ ^ 2 \hat{σ}^2 σ^2)。其缺点是,需要更多的训练样本来充当测试集。
下面的图表示,用验证集法和交叉验证法同样得到了“最佳模型含有6个自变量”的结论。
这里作者还提到了一倍标准差原则(one-standard-error rule)。大致的思路如下:
1)首先计算每种模型大小(即模型中的变量数)对应的测试均方误差(MSE)估计值的标准误差(standard error);
2)然后找到图中最低点对应的那个误差值(即
C
p
C_p
Cp、AIC、BIC等);
3)最后,在最低误差值的一个标准误差区间内,挑选出最简约的模型(也就是变量数量最少的模型)。
这样做的目的是,在误差基本相同的情况下(这里就是定义的一倍标准差的范围),尽可能选择更简单的模型。
(We first calculate the standard error of the estimated test MSE for each model size, and then select the smallest model for which the estimated test error is within one standard error of the lowest point on the curve. The rationale here is that if a set of models appear to be more or less equally good, then we might as well choose the simplest model—that is, the model with the smallest number of predictors)
2.3 正则化法(Shrinkage or Regularization)
与逐步选择法不同,正则化法无需反复模拟不同的变量组合。它从包含所有变量的模型开始,在拟合过程中施加约束条件,迫使无关噪声变量的系数归零,以此达到简化模型的目的。
(As an alternative, we can fit a model containing all p predictors using a technique that constrains or regularizes the coefficient estimates, or equivalently, that shrinks the coefficient estimates towards zero)
最知名的两个方法就是岭回归(ridge regression)和拉索回归(lasso regression)。
(The two best-known techniques for shrinking the regression coefficients towards zero are ridge regression and the lasso)
2.3.1 岭回归(Ridge Regression)
2.3.1.1 岭回归的含义
最小二乘法的拟合过程就是找到
β
0
,
β
1
,
.
.
.
,
β
p
β_0, β_1, . . . , β_p
β0,β1,...,βp,使得下面的
R
S
S
RSS
RSS最小。
岭回归在最小二乘法的基础上增加了一个名为“收缩惩罚”(shrinkage penalty)的惩罚项
λ
∑
j
β
j
2
λ∑_jβ_j^2
λ∑jβj2,也称为
l
2
l_2
l2惩罚,这个惩罚项的目的是使得系数
β
1
,
.
.
.
,
β
p
β_1, . . . , β_p
β1,...,βp趋向于零。
λ
λ
λ是一个调节参数(tuning parameter),用于控制惩罚的强度(The tuning parameter λ serves to control the relative impact of these two terms on the regression coefficient estimates)。
当
λ
=
0
λ=0
λ=0时,惩罚项消失,岭回归退化为普通的最小二乘回归(least square regression);当
λ
λ
λ增大时,惩罚力度增强,迫使系数趋近于零。对于每个
λ
λ
λ值,得到的系数估计都会有所不同(与最小二乘法得到唯一确定的系数值不同),因此选择
λ
λ
λ变得至关重要。通常我们通过交叉验证来选取
λ
λ
λ,这将在后续内容中讨论。需要注意的是,惩罚项不会对模型的截距项(即
β
0
β_0
β0)施加惩罚。
需要特别注意的是,最小二乘法具有尺度等变性(scale invariance)的特点:如果某个变量
X
j
X_j
Xj通过最小二乘法估计得到的系数为
β
j
β_j
βj,当我们将该变量乘以一个常数
c
c
c,再次使用最小二乘法拟合时,新得到的系数将是原系数的
(
1
/
c
)
(1/c)
(1/c)倍,这意味着
β
j
X
j
β_jX_j
βjXj的乘积保持不变。然而,在岭回归中,由于惩罚项的存在,尺度等变性就消失了。因此,在使用岭回归之前,我们通常会对变量进行标准化处理。
下图展示了随着调节参数
λ
λ
λ的增大,标准化后的变量对应的系数值逐渐趋于0。
2.3.1.2 为啥岭回归优于最小二乘回归?
那为什么岭回归就比最小二乘回归的效果好呢?答案就在于偏差与方差的权衡上(Ridge regression’s advantage over least squares is rooted in the bias-variance trade-off)。当 λ λ λ升高时,岭回归的灵活度(或者叫复杂度)会降低,由此会引起偏差(bias)的上升和方差(variance)的下降。(As λ increases, the flexibility of the ridge regression fit decreases, leading to decreased variance but increased bias)
如下图,黑线代表了随着调节参数
λ
λ
λ变化时,模型偏差(bias)的变化情况;绿线则表示模型方差(variance)的变化。当自变量与因变量之间的关系非常接近线性模型时,使用最小二乘法拟合的模型容易出现偏差较小但方差较大的情况,这通常指的是模型过拟合(In general, in situations where the relationship between the response and the predictors is close to linear, the least squares estimates will have low bias but may have high variance)。
然而,在岭回归中,调节参数
λ
λ
λ起到了简化模型和降低方差的作用。因此,在一个合适的
λ
λ
λ区间内,模型简化带来的方差减少通常远远超过了由此引起的偏差增加(whereas ridge regression can still perform well by trading off a small increase in bias for a large decrease in variance)。由于预测误差与模型的方差和偏差之和密切相关(还记得下面的公式吗?),如图中的紫色线,岭回归通常比最小二乘回归能取得更好的效果。
2.3.2 拉索回归(Lasso Regression)
2.3.2.1 拉索回归的定义
岭回归的一个明显缺点是它不具备变量选择的能力,即最终模型会包含所有变量,尽管一些变量的系数可能非常小,但不会精确等于0(除非
λ
λ
λ趋向于无穷大)。在预测精度方面,这不一定是个缺点,但在模型的解释性方面,这确实是一个不利因素(This may not be a problem for prediction accuracy, but it can create a challenge in model interpretation in settings in which the number of variables _p _is quite large)。下面的
R
S
S
+
λ
∑
j
∣
β
j
∣
RSS+λ∑_j|β_j|
RSS+λ∑j∣βj∣是拉索回归需要尽量使其变小的值。
2.3.2.2 拉索回归与岭回归的区别
跟岭回归唯一的区别就是惩罚项里一个是平方项
β
j
2
β_j^2
βj2,一个是绝对值
∣
β
j
∣
|β_j|
∣βj∣,这种叫
l
1
l_1
l1惩罚。跟岭回归一样,调节系数
λ
λ
λ的取值也用交叉验证来决定。从下图中可以看到,随着
λ
λ
λ值的增加,变量的系数逐渐变小,最终变为0,所以说拉索回归有变量筛选的功能。
(The
l
1
l_1
l1penalty has the effect of forcing some of the coefficient estimates to be exactly equal to zero when the tuning parameter λ is sufficiently large. Hence, much like best subset selection, the lasso performs variable selection)

2.3.3 正则化另外一种数学表达
请大家思考一下,下面的这个目标函数所要表达的意思正是最优子集选择法(best subset selection),其中
I
I
I是指标函数,当
β
j
≠
0
β_j≠0
βj=0值为1,否则为0,
∑
j
I
(
β
j
≠
0
)
∑_jI(β_j≠0)
∑jI(βj=0)本质上就表示模型中系数不为0的变量数。
前面我们有谈到,当变量数
p
p
p稍微大一点时,这个目标函数背后的计算量是巨大的。为了减少数据量,我们对约束条件做了改动,于是就有了两种正则化方法。
下面是岭回归的目标函数:
下面是拉索回归的目标函数:
其中约束条件中
s
s
s起到的作用跟前面提到的调节系数
λ
λ
λ是一样。
2.3.4 为啥拉索回归能筛选变量?
根据上节讲到的岭回归和拉索回归的目标函数,学过规划问题的同学应该能记得,我们可以根据约束条件画出可行域。如下图,以两个变量
β
1
β_1
β1和
β
2
β_2
β2为例,拉索回归的可行域表示一个菱形,而岭回归的可行域表示一个圆形。
β
^
\hatβ
β^表示最小二乘法的系数解,周围的红色椭圆表示“等差线”,也就是说在一个红色椭圆上的点具有相同的
R
S
S
RSS
RSS。红色椭圆与蓝色约束区域的交点,就是拉索回归或者岭回归的系数解了。
从图中可以直观地看出,因为拉索回归的可行域“有棱有角”,红色等高线与拉索可行域相交时,很容易发生在坐标轴上,因此会让某个系数直接等于0。但岭回归的可行域是一个圆,与红色等高线相交时一般不会发生在坐标轴上,因此很难让某个系数直接等于0。上面只是简单的二维模型,在高维模型中,存在多个变量同时为0的情况。
(Since ridge regression has a circular constraint with no sharp points, this intersection will not generally occur on an axis, and so the ridge regression coefficient estimates will be exclusively non-zero. However, the lasso constraint has _corners _at each of the axes, andso the ellipse will often intersect the constraint region at an axis. When this occurs, one of the coefficients will equal zero. In higher dimensions, many of the coefficient estimates may equal zero simultaneously)
2.3.5 岭回归和拉索回归谁更厉害?
答案大家应该能猜出来:在机器学习的领域,没有什么方法具有完全统治地位。理论上,当自变量数量较多,且大多数与因变量的相关性较低时(即小部分变量的系数值很大,大部分变量的系数值很低),拉索回归表现更佳;而如果大多数自变量与因变量的相关性较高(即大部分变量的系数都很大),则岭回归表现更优。
(Ridge regression will perform better when the response is a function of many predictors, all with coefficients of roughly equal size. In general, one might expect the lasso to perform better in a setting where a relatively small number of predictors have substantial coefficients, and the remaining predictors have coefficients that are very small or that equal zero)
但有一个悖论是,在现实问题中,我们怎么会事先知道有多少个自变量跟因变量有关呢?所以,咱就不要预先判断了,成年人不做选择,两个都试了再说。
2.3.6 揭示岭回归和拉索回归在系数收缩上的区别
我们用一个非常简单的例子来揭示这两种方法的区别。假设有一个数据集,其变量的数量与样本量相同,那么这个数据集可以被视为一个方阵。我们进一步简化假设,设想这个方阵是一个对角线上元素都为1的对角矩阵,此外为了更好的图形展示,我们也假设回归模型中没有截距。
那么,最小二乘法的目标就是找到一组系数,使得下面的求和表达式最小:
其中的系数解是:![]()
岭回归的目标就是使得下面的求和表达式最小:
其中的系数解是(求导得解,细节就不展开了):![]()
拉索回归的目标就是使得下面的求和表达式最小:
其中的系数解是(分段讨论,细节就不展开了):
下面的两个图直观展示了上面的最小二乘解(黑色虚线表示)、岭回归解(左图红线)、拉索回归解(右图红线),可以看出岭回归就是等比例压缩每个系数的值(左图),然而拉索回归是全部系数值都往0压缩
λ
/
2
λ/2
λ/2个绝对量,原本绝对值小于
λ
/
2
λ/2
λ/2的系数直接变为0。
=
2.3.7 如何挑选调节参数?
很简单,用交叉验证:
1)选择你想尝试的
λ
λ
λ值;
2)针对每一个
λ
λ
λ值,利用交叉验证(一般选5折或者10折)计算模型的验证误差;
3)选择出最小验证误差所对应的那个
λ
λ
λ值;
4)用选择出的
λ
λ
λ值拟合所有的训练样本得到最终的模型。
(Cross-validation provides a simple way to tackle this problem. We choose a grid of λ values, and compute the cross-validation error for each value of λ. We then select the tuning parameter value for which the cross-validation error is smallest. Finally, the model is re-fit using all of the available observations and the selected value of the tuning parameter)
下图是岭回归的交叉验证,垂直的虚线表示交叉验证的误差最小。
下图是拉索回归的交叉验证,垂直的虚线表示交叉验证的误差最小。大家注意下,作者在这里用的横坐标突然变了,其中
β
^
λ
L
\hatβ_λ^L
β^λL表示拉索回归的系数解,
β
^
\hatβ
β^表示最小二乘的系数解。
∣
∣
β
∣
∣
1
||β||_1
∣∣β∣∣1表示
∑
∣
β
j
∣
∑|β_j|
∑∣βj∣,比值等于1,相当于
λ
λ
λ等于0,拉索回归直接等于最小二乘回归;比值越趋近于0,λ值就越大,系数压缩就越厉害。
3. 引用























 1366
1366

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








