CALPHAD方法中“外推”的理解

碎碎念

最初接触到CALPHAD方法的时候，我最大的疑惑就是二元体系的热力学模型是如何整合到三元体系？请教了学长得到的答案是，“把二元的相加在一起就是三元啦。” 当然这个模糊的答案是肯定不会满足我的，但查阅了一些资料得到的答案也不算太能让我信服，有点懒得找了，也就搁置了下来。最近在读数学分析时，看到外推这个词，决定静下心来好好整一下子。

背景介绍

首先提出一个问题，为什么需要研究多元体系？
答：多元合金因为具有多样的微观结构、良好的力学性能等优良特性，在结构和功能材料中得到了广泛的应用。这些合金非常常见，例如Mg合金、Al合金、Ti合金、Fe合金、HEA等。
在《Computer Calculation of Phase Diagrams》有几张相图是公认的准确，那就引出了第二个问题，这些图表是插值还是外推算出？

插值与外推

在数学教材中对于插值和外推的定义是这样的：
插值：估计两个已知值之间的函数值；
外推：基于将已知序列或因子扩展到肯定已知的区域之外的值的估计。
总的来说，估计值与已知值的相对位置决定了估计方法是插值还是外推。例如，一维空间内如果待估计的值在两个已知值之间，则估计方法是插值。
更直观地理解这两个概念，我假设一维空间中有(a,f(a)),(b,f(b))两个点，我们想要估计a点和b点之间的c点就叫插值（interpolation），想要估计这个区间外的d点和e点就叫做外推（extrapolation）。

假设函数为：

$f(x)=w_a(x)f(a)+w_b(x)f(b)$

w_a(x)w_b(x)分别是f(a)f(b)的权重因子。
w_a(x)+w_b(x)=1，假设函数为线性；其他情况，假设函数为非线性。
w_a(x)≥0且w_b(x)≥0，假设方法为插值；其他情况，假设方法为外推。
补充一个小知识点，多元情况下，假设函数可以表达为：

$f(x)={\sum }_{i=1}^{n+1}{w}_i\left(x_i\right)f\left(x_i\right)$

实际相图中的插值与外推

实验不能够测量到不稳定结构的晶格稳定性。那如何在已知的成分、温度和压力范围外估算相平衡？
在文献中得到一个答案，外推或者拓展稳定的相边界估计亚稳相平衡的相变温度。

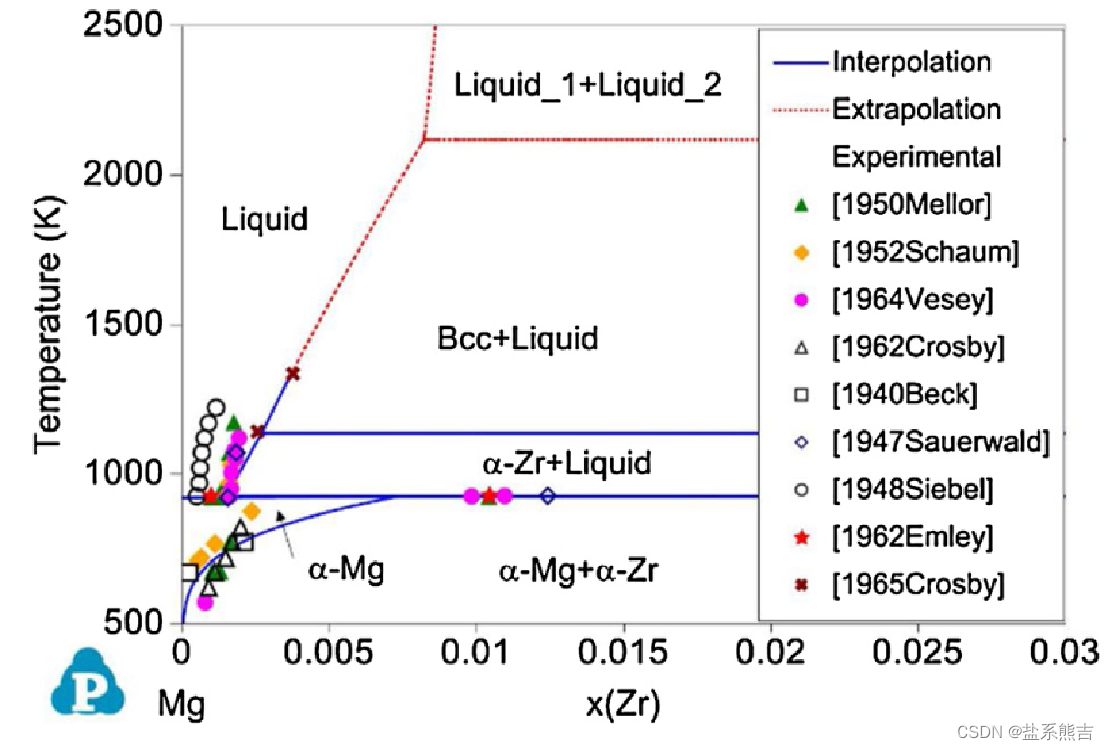
吉布斯能项，例如G_i、G^ex_ij，都和热容、混合热、化学势等相关，并且都是T和P相关的函数。如果所有一元、二元、三元的吉布斯能都在一个T区间和一个P区间内有效，则在这个空间内所有计算都是关于变量T和P的插值。否则就是外推。

二元热力学模型外推到三元的公式推导思路

首先引入一个混合自由能模型——Muggianu Geometric model。

G m = ∑ i X i ln ⁡ X i + R T ∑ i X i ln ⁡ X i + ∑ i j X i X j L i j + ∑ i j k X i X j X k L i j k G_{m} =\sum_{i}^{} X_{i} \ln_{}{X_{i}} +RT\sum_{i}^{} X_{i} \ln_{}{X_{i}} +\sum_{ij}^{} X_{i} X_{j}L_{ij} +\sum_{ijk}^{} X_{i} X_{j} X_{k}L_{ijk} Gm​=∑i​Xi​ln​Xi​+RT∑i​Xi​ln​Xi​+∑ij​Xi​Xj​L