支持向量机的软间隔与正则化

看到西瓜书上有些东西写的不是特别清楚，结合李航的《统计学习方法》，把软间隔与正则化知识点重新整理了一下。
先给出支持向量机的基本形式：$$\begin{array}{rl}& \underset{w,b}{\min }\frac{1}{2}{\Vert w\Vert }^2\\ s.t.& y_i(w^T{x}_i+b)\ge 1,i=1,2,...,m\end{array}$$
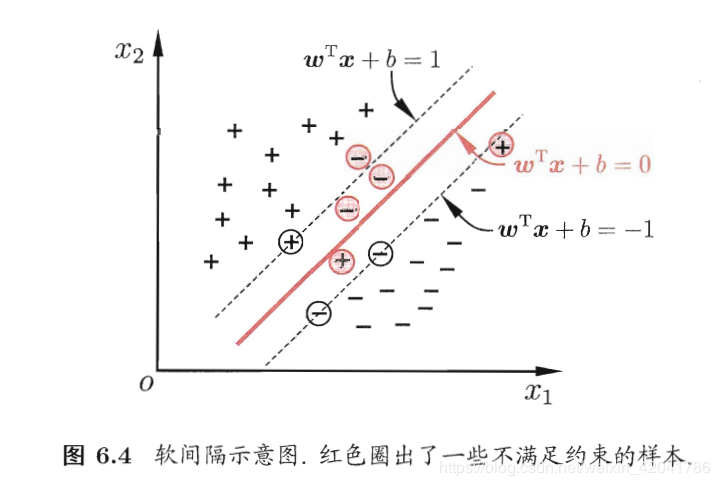
之前支持向量机的普通形式都是假设样本点是线性可分的，也就是说存在一个超平面能将不同类的样本完全划分开，而现实世界中往往很难达到这种要求。我们的解决办法是允许支持向量机在一些样本上出错。由此引出了“软间隔”的概念。如下图：也就意味着某些样本点$(x_i,y_i)$不能满足函数间隔大于等于1的约束条件,有些正样本的点会跑到负样本的区间，有些负样本的会跑到正样本的区间范围。

为了解决这个问题，可以对每个样本点$(x_i,y_i)$引进一个松弛变量${\xi }_i\ge 0$,使函数间隔加上松弛变量大于等于1.也就是$$y_i(w^T{x}_i+b)+{\xi }_i\ge 1$$$$y_i(w^T{x}_i+b)\ge 1-{\xi }_i$$同时，对每个松弛变量${\xi }_i$,支付一个代价${\xi }_i$.目标函数由原来的$\frac{1}{2}{\Vert w\Vert }^2$变成了:$$\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^N{\xi }_i$$,这里的$C>0$称为惩罚参数，变大时对误分类的惩罚增大，减小时对误分类的惩罚减小。上面的最小化目标函数包含两层含义：使$\frac{1}{2}{\Vert w\Vert }^2$尽可能小也就是间隔尽量大，同时使误分类点的个数尽量小，$C$是调和二者的系数，线性不可分的问题就可转化成下面的凸二次规划：$$\begin{array}{rl}& \underset{w,b,\xi }{\min }\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^N{\xi }_i\\ & s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i,i=1,2,...,N\\ & {\xi }_i\ge 0,i=1,2,...,N\end{array}$$上述问题可转化成朗格朗日函数：$$L(w,b,\alpha ,\xi ,\mu )=\frac{1}{2}{\Vert w\Vert }^2+C\sum _{i=1}^N{\xi }_i+\sum _{i=1}^m{\alpha }_i(1-{\xi }_i-y_i(w^T{x}_i+b))-\sum _{i=1}^m{\mu }_i{\xi }_i①$$${\alpha }_i\ge 0$,${\mu }_i\ge 0$是朗格朗日乘子.令$L(w,b,\alpha ,\xi ,\mu )$对$w,b,{\xi }_i$的偏导为0可得：$$\begin{gathered} w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i \\ 0=\sum _{i=1}^m{\alpha }_i{y}_i \\ C={\alpha }_i+{\mu }_i \end{gathered}$$,将上面三个式子代入①式得到原问题的对偶问题：$$\begin{array}{rl}& \underset{\alpha }{\max }\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1}^m\sum _{j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\\ & s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0\\ & 0\le {\alpha }_i\le C,i=1,2,...,m\end{array}$$
还需满足KKT条件：
$$\{\begin{array}{l}{\alpha }_i\ge 0,{\mu }_i\ge 0,\\ y_{i}f(x_i)-1+{\xi }_i\ge 0,\\ {\alpha }_i(y_{i}f(x_i)-1+{\xi }_i)=0,\\ {\xi }_i\ge 0,{\mu }_i{\xi }_i=0\end{array}$$,之后的情况就和线性可分一样了，可用SMO或者其它方法进一步求解。