http://www.ee.cuhk.edu.hk/~xgwang/projectpage_structured_feature_pose.html
Structured Feature Learning for Pose Estimation

Abstract
In this paper, we propose a structured feature learning framework to reason the correlations among body joints at the feature level in human pose estimation.Different from existing approaches of modeling structures on score maps or predicted labels, feature maps preserve substantially richer descriptions of body joints. The relationships between feature maps of joints are captured with the introduced geometrical transform kernels, which can be easily implemented with a convolution layer. Features and their relationships are jointly learned in an end-to-end learning system. A bi-directional tree structured model is proposed, so that the feature channels at a body joint can well receive information from other joints. The proposed framework improves feature learning substantially. With very simple post processing, it reaches the best mean PCP on the LSP and FLIC datasets. Compared with the baseline of learning features at each joint separately with ConvNet, the mean PCP has been improved by 18% on FLIC.
How to cite
@inproceedings{chu2016structure,
title ={Structured Feature Learning for Pose Estimation},
author ={Chu, Xiao and Ouyang, Wanli and Li,Hongsheng and Wang, Xiaogang},
booktitle ={CVPR},
year ={2016},
}
Predictions & Codes
Our paper is now available: [ Paper]
Our results are ready for download: [ Predictions]
The proto files are released: [ Proto Files]
The full code is now available. [ Full code]
Steps to train your own model:
- Make caffe
- Data prepare: run "Data_prepare.m" in MATLAB and then run "ConvertLMDB.sh" to generate LMDB data
- Model training: run "Baseline.sh"
- TestModel: Select one model and write the directory in "TestModel.m", run "TestModel.m"
Experimetal Results
| Method | Torso | Head | Upper Arms | Lower Arms | Upper Legs | Lower Legs | Mean |
|---|---|---|---|---|---|---|---|
| Ours | 95.4 | 89.6 | 77.0 | 65.2 | 87.6 | 83.2 | 81.1 |
| Xianjie Chen et al., NIPS'14 | 92.7 | 87.8 | 69.2 | 55.4 | 82.9 | 77.0 | 75.0 |
| Pishchulin et al., ICCV'13 | 88.7 | 85.6 | 61.5 | 44.9 | 78.8 | 73.4 | 69.2 |
| Ouyang et al., CVPR'14 | 85.8 | 83.1 | 63.3 | 46.6 | 76.5 | 72.2 | 68.6 |
| Ramakrishna et al., ECCV'14 | 88.1 | 80.9 | 62.3 | 39.1 | 78.9 | 73.4 | 67.6 |
| Eichner&Ferrari, ACCV'12 | 86.2 | 80.1 | 56.5 | 37.4 | 74.3 | 69.3 | 64.3 |
| Pishchulin et al., CVPR'13 | 87.5 | 78.1 | 54.2 | 33.9 | 75.7 | 68.0 | 62.9 |
| Yang&Ramanan, CVPR'11 | 84.1 | 77.1 | 52.5 | 35.9 | 69.5 | 65.6 | 60.8 |
| Kiefel&Gehler, ECCV'14 | 84.4 | 78.4 | 53.3 | 27.4 | 74.4 | 67.1 | 60.7 |
| Method | Upper Arms | Lower Arms | Mean |
|---|---|---|---|
| Ours | 97.9 | 92.4 | 95.2 |
| Xianjie Chen et al., NIPS'14 | 97.0 | 86.8 | 91.9 |
| Tompson et al., NIPS'14 | 93.7 | 80.9 | 87.3 |
| MODEC, CVPR'13 | 84.4 | 52.1 | 68.3 |
Comparison of PDJ curves of elbows and wrists on the Frames Labeled In Cinema (FLIC) Dataset using Observer-Centric (OC) annotations. The curves are for Xianjie Chen et al., NIPS'14, Tompson et al., NIPS'14, DeepPose, CVPR'14, and MODEC, CVPR'13.
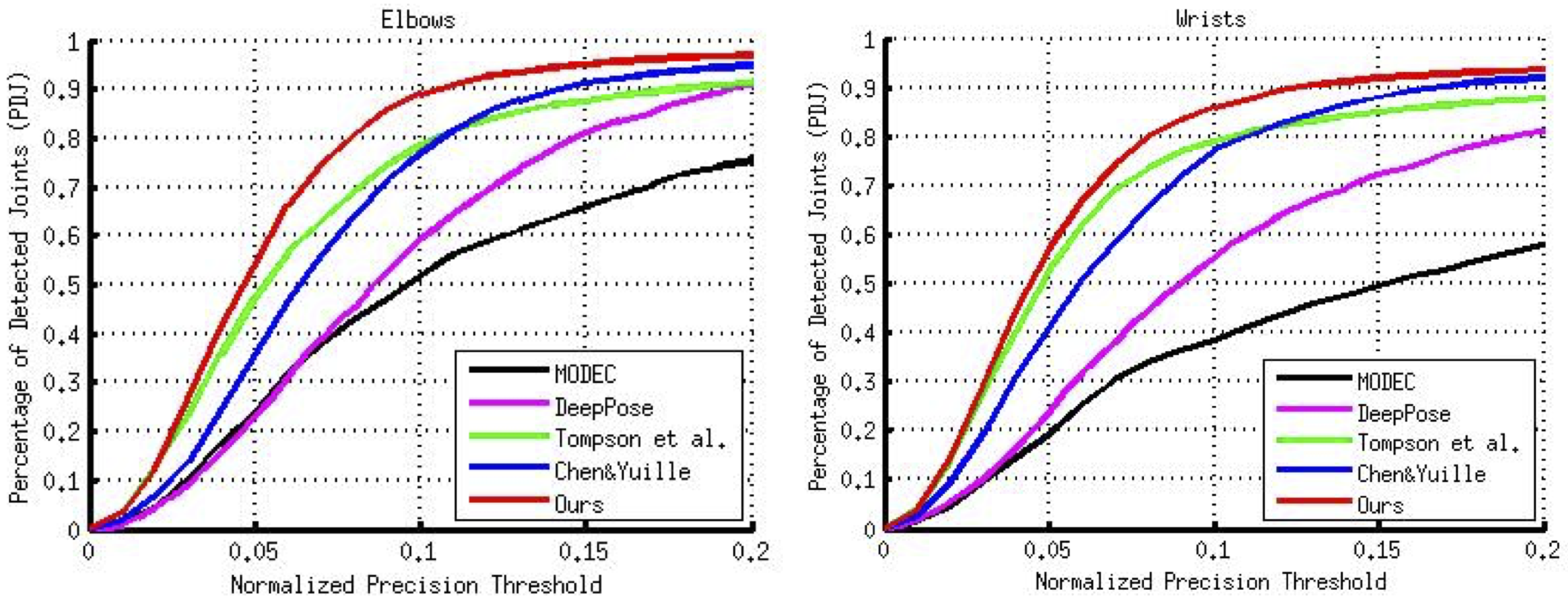

Our method
1. Motivation:
Independent prediction of body joint locations from appearance score maps can be refined by modeling the spatial relationship among correlated body joints. On score maps, the information at a location is summarized into a single probability value, while detailed information indicating the attritbutes of the body joint is missing. These information is valuable for the structural learning among body joints much less effective. We observe that these types of information are well preserved at the feature level. As shown in Fig. 2 on the right.
Independent prediction of body joint locations from appearance score maps can be refined by modeling the spatial relationship among correlated body joints. On score maps, the information at a location is summarized into a single probability value, while detailed information indicating the attritbutes of the body joint is missing. These information is valuable for the structural learning among body joints much less effective. We observe that these types of information are well preserved at the feature level. As shown in Fig. 2 on the right.

Figure 2. Examples of response maps of different images to the same feature channels. (a) A feature channel for the neck. (b) A feature channel for the left wrist. (c) A feature channel for the left lower arm.
2. Geometrical transfer kenerls:
We show that under a fully convolutional neural network, messages can be passed between feature maps through the introduced geometrical transform kernels. The FCN filters and the kernels can be jointly learned. convolution with asymmetric kernels could geometrically shift the feature responses. (a) is a feature map assuming Gaussian distribution. (b) are different kernels for illustration. (c) are the transformed feature maps after convolution. The feature map has been shifted towards different directions and sum up to different values.
We show that under a fully convolutional neural network, messages can be passed between feature maps through the introduced geometrical transform kernels. The FCN filters and the kernels can be jointly learned. convolution with asymmetric kernels could geometrically shift the feature responses. (a) is a feature map assuming Gaussian distribution. (b) are different kernels for illustration. (c) are the transformed feature maps after convolution. The feature map has been shifted towards different directions and sum up to different values.
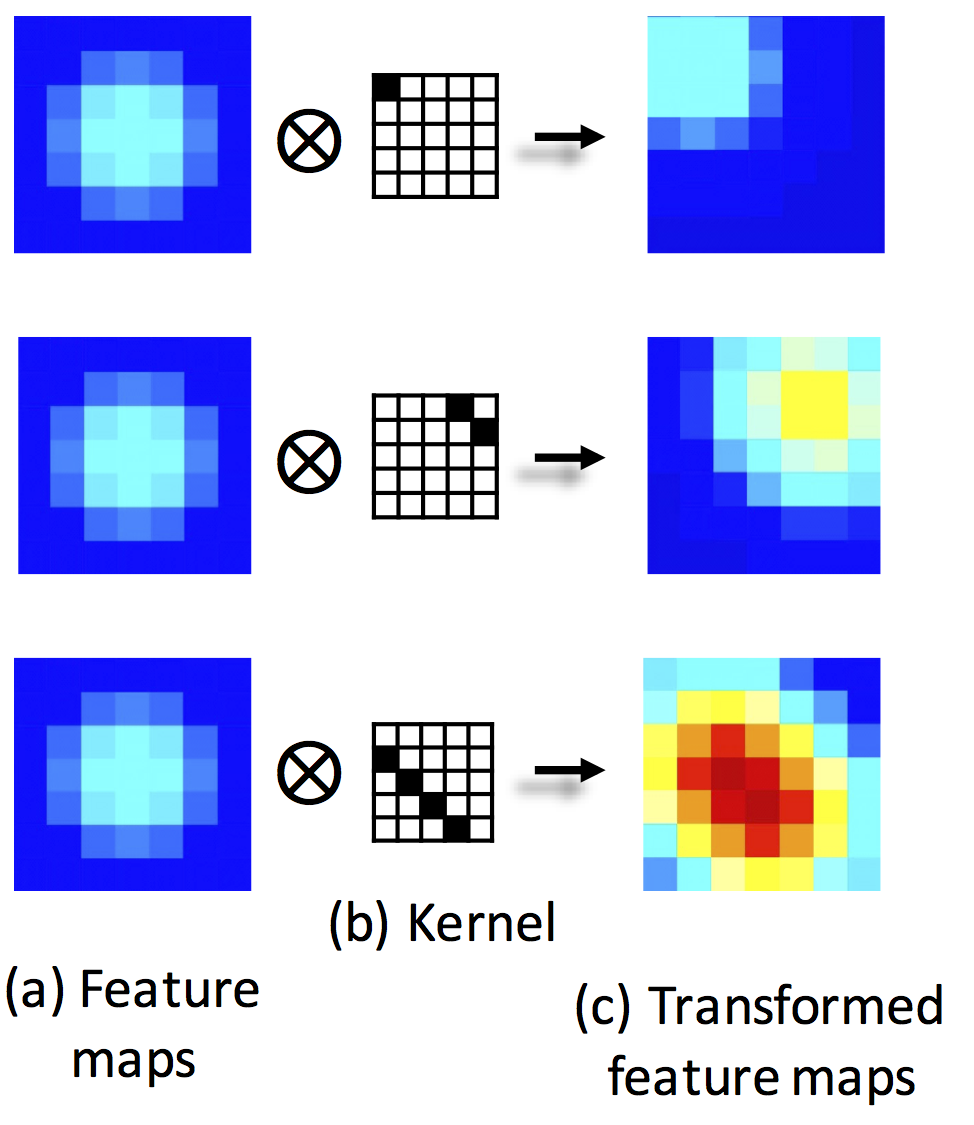
Figure 3.
3. Feature updatae:
We propose to build up dependency at feature level. The process of how one set of feauture map influence another is shown in Fig. 4. These kernels can be implemented with convolution and the relationships can be learned in and end-to-end learning system.
We propose to build up dependency at feature level. The process of how one set of feauture map influence another is shown in Fig. 4. These kernels can be implemented with convolution and the relationships can be learned in and end-to-end learning system.
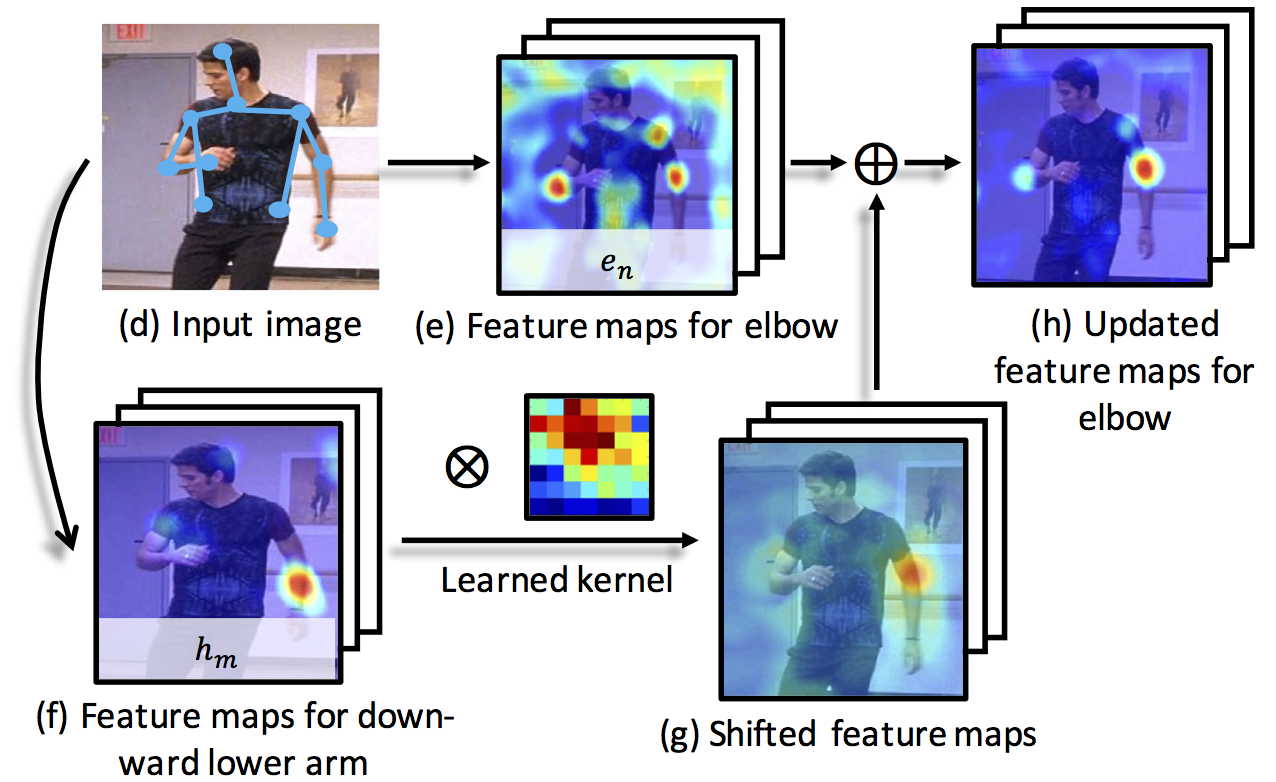
Fig. 4. An example of updating feature maps by passing information between joints
4. Bidirectional Tree:
It is important to design proper information flow between body joints, so that features at a joint can be optimized by receiving messages from highly correlated joints and will not be disturbed by less correlated joints in distance. A bi-directional tree-structured model is proposed. The pro- posed model connects correlated joints and passes messages in both directions along the tree. Therefore, every joint can receive information from all the neighboring joints. (1) Original feature maps for body joints. (2) Refine the feature maps by information passing in a structure feature learning layer. (2,a) and (2,b) show the details of the bi-directional tree which have information flows in opposite directions. The process of updating feature maps are also illustrated. (3) Predict score maps for joints based on feature maps. Dashed line is copy operation and solid line is convolution.
It is important to design proper information flow between body joints, so that features at a joint can be optimized by receiving messages from highly correlated joints and will not be disturbed by less correlated joints in distance. A bi-directional tree-structured model is proposed. The pro- posed model connects correlated joints and passes messages in both directions along the tree. Therefore, every joint can receive information from all the neighboring joints. (1) Original feature maps for body joints. (2) Refine the feature maps by information passing in a structure feature learning layer. (2,a) and (2,b) show the details of the bi-directional tree which have information flows in opposite directions. The process of updating feature maps are also illustrated. (3) Predict score maps for joints based on feature maps. Dashed line is copy operation and solid line is convolution.
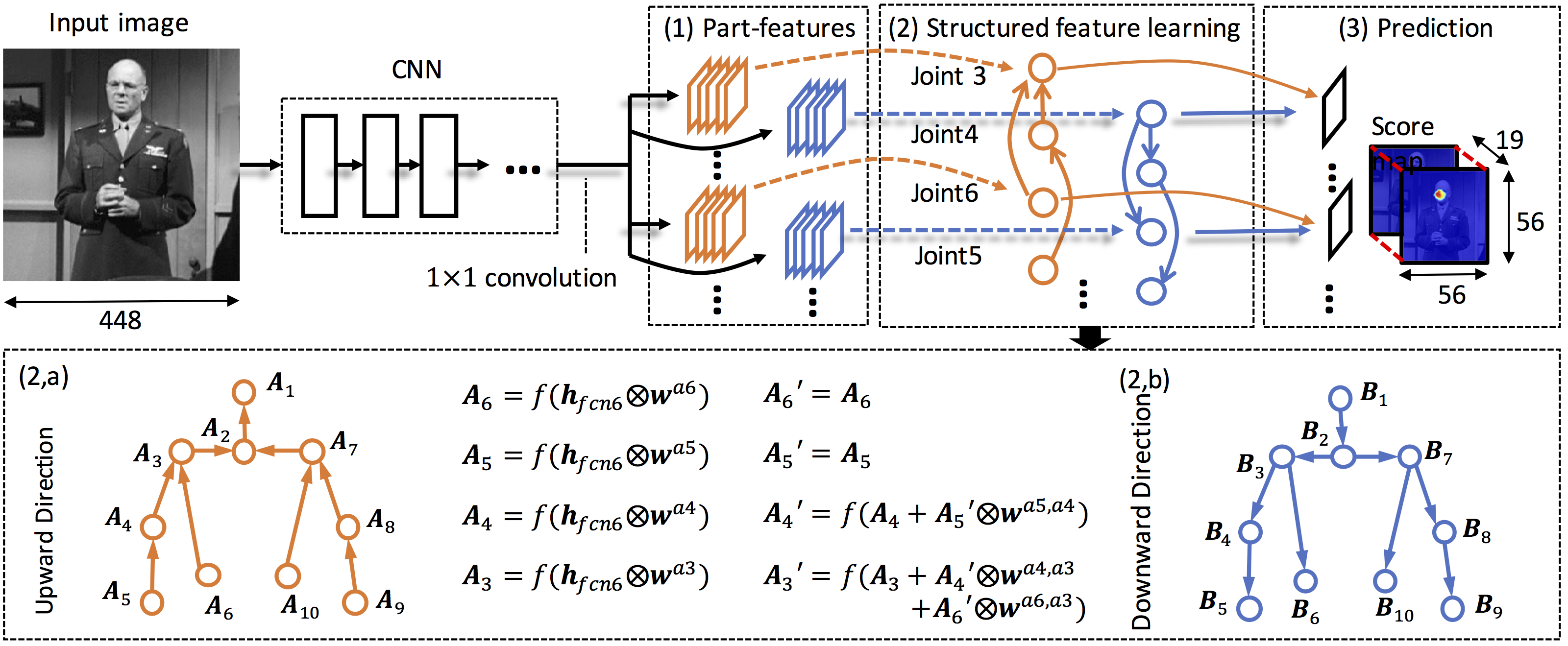
Fig. 5. Our pipeline for pose estimation.
Quick links to related work
Efficient Object Localization Using Convolutional Networks, J. Tompson, R. Goroshin, A. Jain, Y. LeCun, C. Bregler, CVPR'15Articulated Pose Estimation by a Graphical Model with Image Dependent Pairwise Relations, Xianjie Chen and Alan Yuille, NIPS'14
Nice Performance Evaluation by Pishchulin et al.(MPII Human Pose Dataset)
Leeds Sports Pose Dataset (LSP)
Frames Labeled In Cinema Dataset (FLIC)























 4815
4815

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








