1. 镜像频率的产生
在使用AWG发射正弦波的时候会不可避免的产生镜像频率,当发射频率靠近奈奎斯特频率时,会产生严重的镜像效应,那么镜像频率到底是怎么产生的呢?假设
A
W
G
AWG
AWG的发射采样率为
f
s
f_{s}
fs,发射的正弦波的幅值为
A
A
A,频率的
f
0
f_{0}
f0,初相位
φ
0
\varphi_{0}
φ0,那么发射的数字信号可以表示为:
x
[
k
]
=
A
sin
(
2
π
f
0
f
s
k
+
φ
0
)
=
−
A
sin
(
2
π
f
s
−
f
0
f
s
k
−
φ
0
)
=
A
sin
(
2
π
f
s
−
f
0
f
s
k
+
(
π
−
φ
0
)
)
\begin{aligned}x[k] &= A\sin\left(2\pi\frac{f_{0}}{f_{s}}k+\varphi_{0}\right)\\&=-A\sin\left(2\pi\frac{f_{s}-f_{0}}{f_{s}}k-\varphi_{0}\right)\\&=A\sin\left(2\pi\frac{f_{s}-f_{0}}{f_{s}}k+\left(\pi-\varphi_{0}\right)\right)\end{aligned}
x[k]=Asin(2πfsf0k+φ0)=−Asin(2πfsfs−f0k−φ0)=Asin(2πfsfs−f0k+(π−φ0))
由上式可将,当
A
W
G
AWG
AWG发射一个频率为
f
0
f_{0}
f0的正弦波时,就相当于发射了一个频率为
f
s
−
f
0
f_{s}-f_{0}
fs−f0的带有相移为
Δ
φ
=
π
−
2
φ
0
\Delta\varphi = \pi-2\varphi_{0}
Δφ=π−2φ0的正弦波。当
f
0
f_{0}
f0较小时,镜像
f
s
−
f
0
f_{s}-f_{0}
fs−f0在第二奈奎斯特区域的远端,此时二者能量差异较大且频率间隔较大,对信号的干扰较小;但是当
f
0
f_{0}
f0靠近第
f
s
/
2
f_{s}/2
fs/2时,镜像
f
s
−
f
0
f_{s}-f_{0}
fs−f0靠近第二奈奎斯特区域的近端,此时二者能量差异较小,且频率差异较小,对信号的干扰较大;示意图如下。
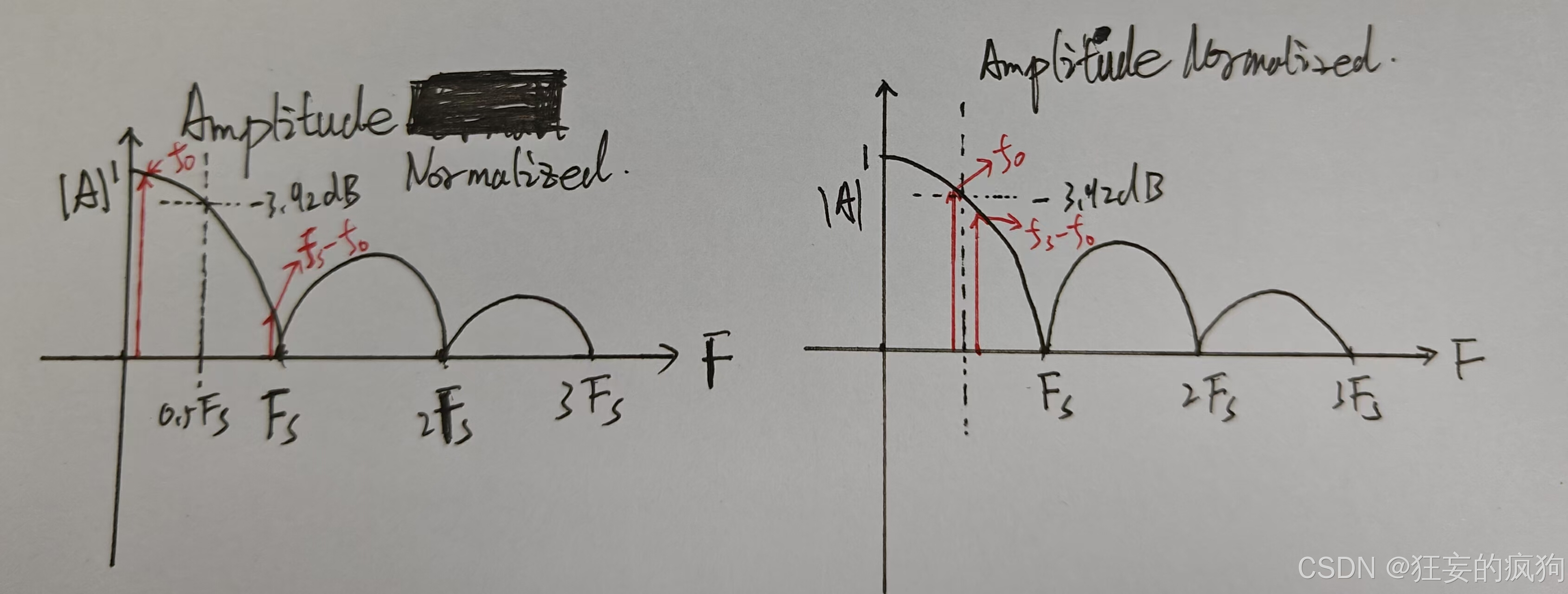
2. 镜像成对出现
实际上镜像频率在整个频带上都是与信号的谐波成对出现的,基于上面的公式不难得到这个结果,此处就不做详细的分析了,下面是一个仿真的结果

s i n e w a v e sinewave sinewave频率为 2.3 G H z 2.3\ GHz 2.3 GHz,发射采样率为 5 G H z 5\ GHz 5 GHz,分析带宽为 40 G H z 40\ GHz 40 GHz,可见镜像与谐波成对出现
下面是两个实测的结果
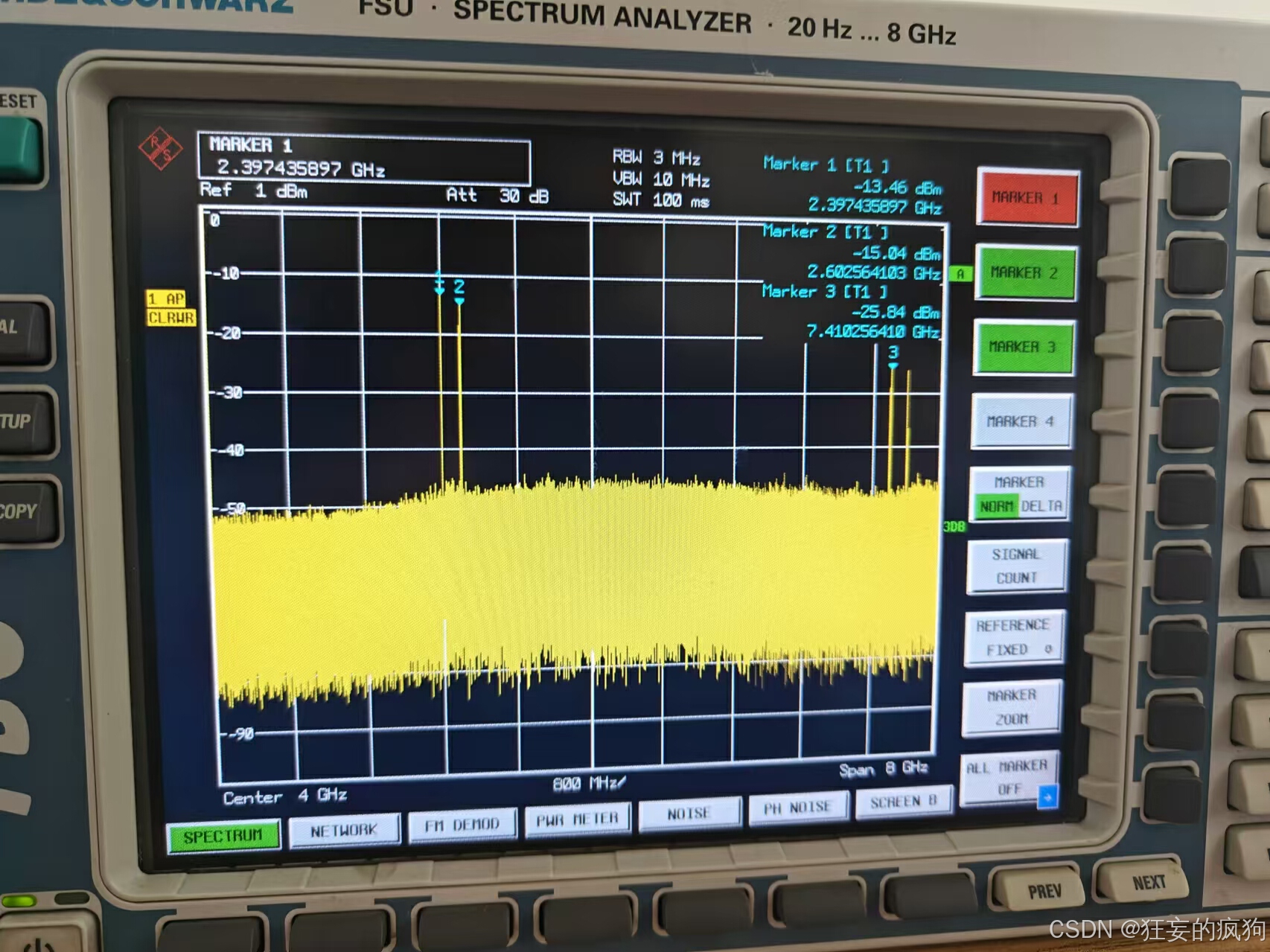 s
i
n
e
w
a
v
e
sinewave
sinewave频率为
2.4
G
H
z
2.4\ GHz
2.4 GHz,发射采样率为
5
G
H
z
5\ GHz
5 GHz,分析带宽为
8
G
H
z
8\ GHz
8 GHz
s
i
n
e
w
a
v
e
sinewave
sinewave频率为
2.4
G
H
z
2.4\ GHz
2.4 GHz,发射采样率为
5
G
H
z
5\ GHz
5 GHz,分析带宽为
8
G
H
z
8\ GHz
8 GHz
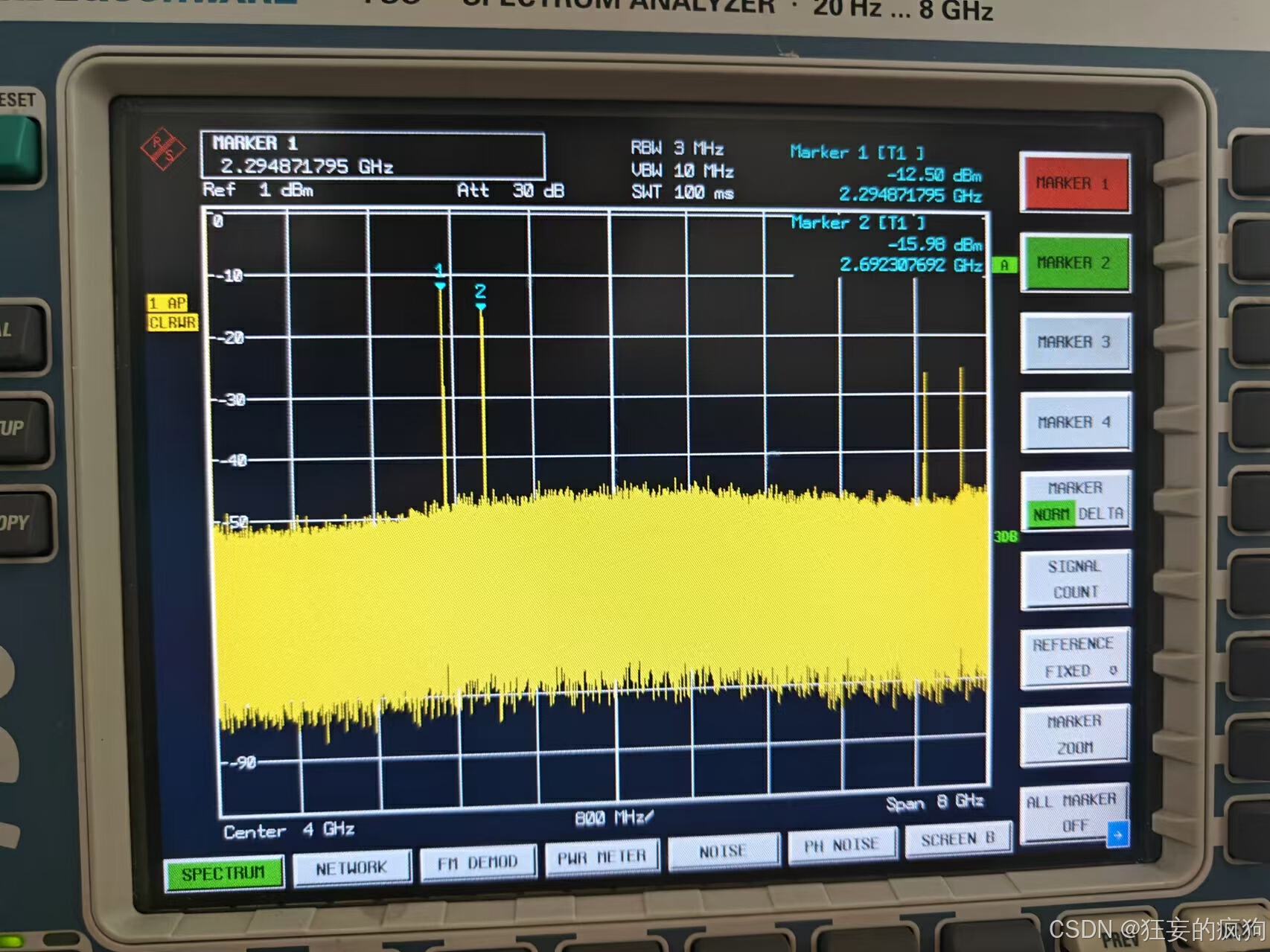
s i n e w a v e sinewave sinewave频率为 2.3 G H z 2.3\ GHz 2.3 GHz,发射采样率为 5 G H z 5\ GHz 5 GHz,分析带宽为 8 G H z 8\ GHz 8 GHz























 6916
6916

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








