存在站址误差下TDOA定位的CRLB

存在站址误差下观测模型

在三维直角坐标系中，考虑利用M个观测站对一个目标进行定位。
第i个观测站位置向量记为 ${\mathbf{s}}_i^o=[s_{x,i}^o,s_{y,i}^o,s_{z,i}^o{]}^T,1\le i\le M$，目标位置向量记为${\mathbf{u}}^o=[u_x^o,u_y^o,u_z^o{]}^T$

将第一个观测站作为TDOA测量的参考观测站，则目标到达其余观测站和参考观测站之间的TDOA可以表示为：
$${\tau }_{j1}^o=\frac{||{\mathbf{u}}^o-{\mathbf{s}}_j^o|{|}_2}{c}-\frac{||{\mathbf{u}}^o-{\mathbf{s}}_1^o|{|}_2}{c},2\le j\le M$$
其中c表示信号传播速度，通常是已知的，因此TDOA可以转换为到达距离差（Range Difference Of Arrival，RDOA）：
$$r_{j1}^o=||{\mathbf{u}}^o-{\mathbf{s}}_j^o|{|}_2-||{\mathbf{u}}^o-{\mathbf{s}}_1^o|{|}_2,2\le j\le M$$
因此建立RDOA观测模型为：
$$\mathbf{r}={\mathbf{r}}^{\mathbf{o}}+{\mathbf{n}}_{\mathbf{r}}=[r_{21}^o,r_{31}^o,...,r_{M1}^o{]}^T+[\delta r_{21},\delta r_{31},...,\delta r_{M1}{]}^T$$
${\mathbf{n}}_{\mathbf{r}}$表示测量噪声向量，协方差矩阵表示为$\mathbf{Q}$。

在实际过程中，观测站可能处于运动状态，从而获得的观测站位置是带有误差的，将带有误差的观测站位置建模为：${\mathbf{s}}_{\mathbf{i}}={\mathbf{s}}_{\mathbf{i}}^{\mathbf{o}}+{\mathbf{n}}_{{\mathbf{s}}_{\mathbf{i}}}=[s_{i,x}^o,s_{i,y}^o,s_{i,z}^o{]}^T+[\delta s_{i,x},\delta s_{i,y},\delta s_{i,z}{]}^T$。其中${\mathbf{s}}_{\mathbf{i}}^{\mathbf{o}}$表示观测站真实位置向量，${\mathbf{n}}_{{\mathbf{s}}_{\mathbf{i}}}$表示随机误差。则将所有观测站向量组合得到：
$$\mathbf{s}={\mathbf{s}}^o+{\mathbf{n}}_{\mathbf{s}}=[({\mathbf{s}}_1^{\mathbf{o}}{)}^T,({\mathbf{s}}_2^{\mathbf{o}}{)}^T,...,({\mathbf{s}}_{\mathbf{M}}^{\mathbf{o}}{)}^T{]}^T+[{\mathbf{n}}_{{\mathbf{s}}_1}^{\mathbf{T}},{\mathbf{n}}_{{\mathbf{s}}_2}^{\mathbf{T}},...,{\mathbf{n}}_{{\mathbf{s}}_{\mathbf{M}}}^{\mathbf{T}}{]}^T$$
${\mathbf{n}}_{\mathbf{s}}$的协方差矩阵表示为${\mathbf{Q}}_{\mathbf{s}}$。

站址误差下的DOA定位的CRLB

存在站址误差时的未知向量为${\mathbf{\kappa }}^o=[({\mathbf{u}}^o{)}^T,({\mathbf{s}}^o{)}^T{]}^T$，测量向量为TDOA测量值，记为$\mathbf{r}$。则此时对数似然函数表示为：
$$ln(p(\mathbf{r}|{\mathbf{\kappa }}^o))=\kappa -(1/2)(\mathbf{r}-{\mathbf{r}}^o{)}^T{\mathbf{Q}}^{-1}(\mathbf{r}-{\mathbf{r}}^o)-(1/2)(\mathbf{s}-{\mathbf{s}}^o{)}^T{\mathbf{Q}}_{\mathbf{s}}^{-1}(\mathbf{s}-{\mathbf{s}}^o)$$
Fisher信息矩阵表示为：
$$\mathbf{F}=\begin{array}{c}\left[\begin{array}{cc}{\mathbf{F}}_1& {\mathbf{F}}_2\\ {\mathbf{F}}_2^T& {\mathbf{F}}_3\end{array}\right]\end{array}$$
其中：
$$\{\begin{array}{l}{\mathbf{F}}_1=\left(\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{u}}^{\mathbf{o}}{)}^T}\right){\mathbf{Q}}^{-1}{\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{u}}^{\mathbf{o}}{)}^T}\right)}^T\right)\\ {\mathbf{F}}_2=\left(\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{u}}^{\mathbf{o}}{)}^T}\right){\mathbf{Q}}^{-1}{\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{s}}^{\mathbf{o}}{)}^T}\right)}^T\right)\\ {\mathbf{F}}_3=\left(\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{s}}^{\mathbf{o}}{)}^T}\right){\mathbf{Q}}^{-1}{\left(\frac{\partial {\mathbf{r}}^{\mathbf{o}}}{\partial ({\mathbf{s}}^{\mathbf{o}}{)}^T}\right)}^T\right)+{\mathbf{Q}}_{\mathbf{s}}^{-1}\end{array}$$
存在站址误差下的TDOA定位CRLB表示为：

$$\mathbf{CRLB}=\begin{array}{c}\left[\begin{array}{cc}{\mathbf{X}}_1& {\mathbf{X}}_2\\ {\mathbf{X}}_2^T& {\mathbf{X}}_3\end{array}\right]\end{array}$$
其中：
$$\mathbf{CRLB}({\mathbf{u}}^o)={\mathbf{X}}_1={\left({\mathbf{F}}_1-{\mathbf{F}}_2{\mathbf{F}}_3^{-1}{\mathbf{F}}_2^T\right)}^{-1}={\mathbf{F}}_1^{-1}+{\mathbf{F}}_1^{-1}{\mathbf{F}}_2{\left({\mathbf{F}}_3-{\mathbf{F}}_2^T{\mathbf{F}}_1^{-1}{\mathbf{F}}_2\right)}^{-1}{\mathbf{F}}_2^T{\mathbf{F}}_1^{-1}$$

$$\mathbf{CRLB}({\mathbf{s}}^o)={\mathbf{X}}_3={\left({\mathbf{F}}_3-{\mathbf{F}}_2{\mathbf{F}}_1^{-1}{\mathbf{F}}_2^T\right)}^{-1}={\mathbf{F}}_3^{-1}+{\mathbf{F}}_3^{-1}{\mathbf{F}}_2{\left({\mathbf{F}}_1-{\mathbf{F}}_2^T{\mathbf{F}}_3^{-1}{\mathbf{F}}_2\right)}^{-1}{\mathbf{F}}_2^T{\mathbf{F}}_3^{-1}$$
$\mathbf{CRLB}({\mathbf{u}}^o)$ 表示目标估计的CRLB，$\mathbf{CRLB}({\mathbf{s}}^o)$表示观测站估计的CRLB。

matlab仿真

clc;
clear all;
close all;
%%
% 测向站数量
M=6;
% 目标数量
N=1;
% 光速m/s
c=3*10^8;
s1=[1500 -1900 1400].';
s2=[-1600 2000 1700].';
s3=[1800 -1500 -1600].';
s4=[-1200 1400 -2000].';
s5=[1700 1600 2000].';
s6=[-1800 -1400 -1800].';
% 目标位置
u1=[4000 4000 3000].';

S1=[0,1,0].';
S2=[1,0,0].';
S3=[0,0,1].';
%%     对目标位置的导数
% 时差对目标位置的导数
differ_t_u=zeros(M-1,3);
diff_s1_u1=u1-s1;
for i=2:M
    %     组合字符串，得到接收站的变量名，以便循环
    str_si=['s',mat2str(i)];
    %    返回变量名对应的值
    si_value=eval(str_si);   
    diff_si_u=u1-si_value;
    differ_t_u(i-1,:)=diff_si_u.'/osjl(u1,si_value)-diff_s1_u1.'/osjl(u1,s1);
end

F_u=[differ_t_u];

%%     对观测站位置的导数
% 时差
differ_t_s=zeros(M-1,3*M);
diff_s1_u1=u1-s1;
for i=2:M
    %     组合字符串，得到接收站的变量名，以便循环
    str_si=['s',mat2str(i)];
    %    返回变量名对应的值
    si_value=eval(str_si);
    
    diff_si_u=u1-si_value;
    differ_t_s(i-1,1:3)=diff_s1_u1.'/osjl(u1,s1);
    differ_t_s(i-1,3*(i-1)+1:3*(i-1)+3)=-diff_si_u.'/osjl(u1,si_value);
end
F_s=[differ_t_s];
%%
deta1_more=1:5:50;
for jjj=1:1:length(deta1_more)    
    deta_s=10;
    Rs_a=deta_s^2*eye(3*M,3*M);
    
    deta_r=deta1_more(jjj);
    R_t_a=(deta_r)^2*(eye(M-1,M-1)+ones(M-1,M-1))/2;
     
    Rn_a=blkdiag(R_t_a);
    
    F1=F_u.'*inv(Rn_a)*F_u;
    F2=F_u.'*inv(Rn_a)*F_s;
    F3=F_s.'*inv(Rn_a)*F_s+inv(Rs_a);
    
    CRLB_a=inv(F1-F2*inv(F3)*F2.');
    crb_a(1,jjj)=(sqrt(trace(CRLB_a)));    
    
    CRLB_b=inv(F1);
    crb_b(1,jjj)=sqrt(trace(CRLB_b));
end
figure
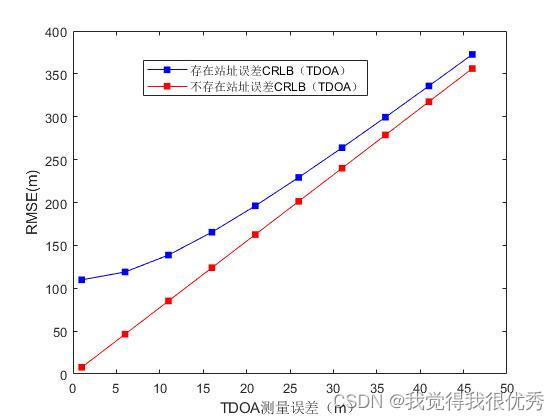
plot(deta1_more,crb_a,'b.-','MarkerSize',15)
hold on;
plot(deta1_more,crb_b,'r.-','MarkerSize',15)
xlabel('TDOA测量误差（m）')
ylabel('RMSE(m)')
% ylim([0 160])
legend('存在站址误差CRLB（TDOA）','不存在站址误差CRLB（TDOA）')
%%
function [distance]=osjl(object,source)
% 输入均为列向量
distance=sqrt(sum((object-source).^2));
end

clc;
clear all;
close all;
%%
% 测向站数量
M=6;
% 目标数量
N=1;
% 光速m/s
c=3*10^8;
s1=[1500 -1900 1400].';
s2=[-1600 2000 1700].';
s3=[1800 -1500 -1600].';
s4=[-1200 1400 -2000].';
s5=[1700 1600 2000].';
s6=[-1800 -1400 -1800].';
% 目标位置
u1=[4000 4000 3000].';

S1=[0,1,0].';
S2=[1,0,0].';
S3=[0,0,1].';
%%     对目标位置的导数
% 时差对目标位置的导数
differ_t_u=zeros(M-1,3);
diff_s1_u1=u1-s1;
for i=2:M
    %     组合字符串，得到接收站的变量名，以便循环
    str_si=['s',mat2str(i)];
    %    返回变量名对应的值
    si_value=eval(str_si);   
    diff_si_u=u1-si_value;
    differ_t_u(i-1,:)=diff_si_u.'/osjl(u1,si_value)-diff_s1_u1.'/osjl(u1,s1);
end

F_u=[differ_t_u];

%%     对观测站位置的导数
% 时差
differ_t_s=zeros(M-1,3*M);
diff_s1_u1=u1-s1;
for i=2:M
    %     组合字符串，得到接收站的变量名，以便循环
    str_si=['s',mat2str(i)];
    %    返回变量名对应的值
    si_value=eval(str_si);
    
    diff_si_u=u1-si_value;
    differ_t_s(i-1,1:3)=diff_s1_u1.'/osjl(u1,s1);
    differ_t_s(i-1,3*(i-1)+1:3*(i-1)+3)=-diff_si_u.'/osjl(u1,si_value);
end
F_s=[differ_t_s];
%%
deta1_more=1:5:50;
for jjj=1:1:length(deta1_more)    
    deta_s=deta1_more(jjj);
    Rs_a=deta_s^2*eye(3*M,3*M);
    
    deta_r=10;
    R_t_a=(deta_r)^2*(eye(M-1,M-1)+ones(M-1,M-1))/2;
     
    Rn_a=blkdiag(R_t_a);
    
    F1=F_u.'*inv(Rn_a)*F_u;
    F2=F_u.'*inv(Rn_a)*F_s;
    F3=F_s.'*inv(Rn_a)*F_s+inv(Rs_a);
    
    CRLB_a=inv(F1-F2*inv(F3)*F2.');
    crb_a(1,jjj)=(sqrt(trace(CRLB_a)));    
    
    CRLB_b=inv(F1);
    crb_b(1,jjj)=sqrt(trace(CRLB_b));
end
figure
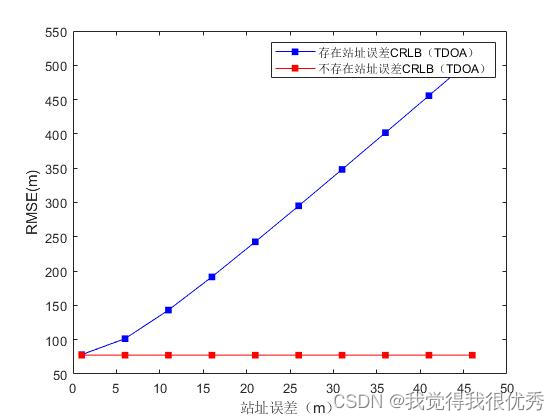
plot(deta1_more,crb_a,'b.-','MarkerSize',15)
hold on;
plot(deta1_more,crb_b,'r.-','MarkerSize',15)
xlabel('TDOA测量误差（m）')
ylabel('RMSE(m)')
% ylim([0 160])
legend('存在站址误差CRLB（TDOA）','不存在站址误差CRLB（TDOA）')
%%
function [distance]=osjl(object,source)
% 输入均为列向量
distance=sqrt(sum((object-source).^2));
end

参考：
DOA定位CRLB
TDOA定位CRLB
存在站址误差的DOA定位CRLB