回归是在建模过程中用于分析变量之间的关系、以及变量是如何影响结果的一种分析方法。
常见的五种回归方法:线性回归(linear regression)、多项式回归(ploynomia regressionl)、岭回归(ridge regression)、Lasso回归和弹性回归网络
1 线性回归
线性回归是指全部由线性变量组成的回归模型,例如单变量线性回归模型
Y
=
a
∗
X
+
b
Y=a∗X+b
Y=a∗X+b
多变量线性回归模型:
Y
=
a
1
∗
X
1
+
a
1
∗
X
2
+
a
3
∗
X
3
+
.
.
.
.
.
+
a
n
∗
X
n
+
b
Y=a1∗X1+a1∗X2+a3∗X3+.....+an∗Xn+b
Y=a1∗X1+a1∗X2+a3∗X3+.....+an∗Xn+b
其中a为系数,x是变量,b为偏置。因为这个函数只有线性关系,所以只适用于建模线性可分数据。我们只是使用系数权重来加权每个特征变量的重要性。我们使用随机梯度下降(SGD)来确定这些权重a和偏置b,过程如图所示:

线性回归的几个特点:
- 建模速度快,不需要很复杂的计算,在数据量大的情况下依然运行速度很快。
- 可以根据系数给出每个变量的理解和解释
- 对异常值很敏感
2 多项式回归
线性回归适合于线性可分的数据,当我们处理非线性可分的数据时可以使用多项式回归。在这种回归中,我们是要找到一条曲线来拟合数据点,可以表示成下面的式子:
Y
=
a
1
∗
X
1
+
a
2
∗
X
2
+
a
3
∗
X
3
+
.
.
.
+
a
n
∗
X
n
+
b
Y=a_1∗X_1+a_2∗X_2+a_3∗X_3+...+a_n∗X_n+b
Y=a1∗X1+a2∗X2+a3∗X3+...+an∗Xn+b
选择每个变量的确切的质数需要当前数据集合与最终输出的一些先验知识。下面两个图描述了线性回归与多项式回归的比较:

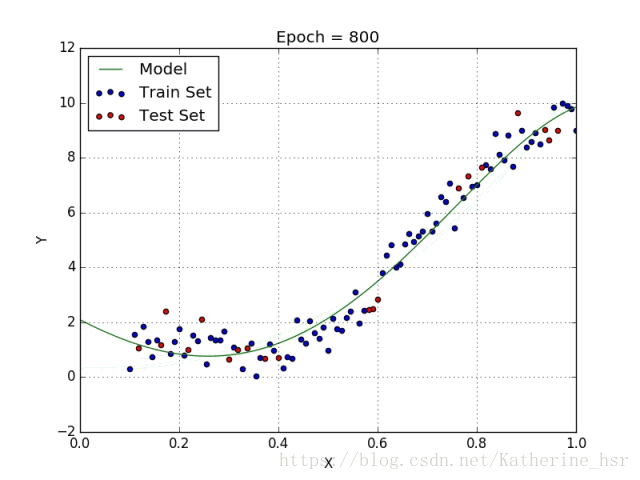
多项式回归的目标函数:最小化残差平方和,通过求偏导解优化问题。

多项式回归的特点:
- 能够拟合非线性可分的数据,更加灵活的处理复杂的关系
- 因为需要设置变量的指数,所以它是完全控制要素变量的建模
- 需要一些数据的先验知识才能选择最佳指数
- 如果指数选择不当容易出现过拟合
3 岭回归(Ridge regression)
共线性:collinearity,自变量之间存在着线性关系,这样就会对回归分析造成影响。
高共线性就是指,自变量之间存在着某种函数关系,这样就不能得到单一变量对结果的影响了。因此需要先排除高共线性,高共线性的判断可以通过以下方法进行:
- 尽管从理论上讲,该变量与Y高度相关,但是回归系数却不明显
- 添加或删除X特征变量时,回归系数会发生明显变化
- X特征变量具有较高的成对相关性(pairwise correlations)(检查相关矩阵)
标准线性回归的优化函数如下:
m
i
n
∣
∣
X
w
−
y
∣
∣
2
min||Xw−y||^2
min∣∣Xw−y∣∣2
其中X表示特征变量,w表示权重,y表示真实情况。岭回归是针对模型中存在的共线性关系的为变量增加一个小的平方偏差因子(也就是正则项),可以表示成下面的式子:
m
i
n
∣
∣
X
w
−
y
∣
∣
2
+
z
∣
∣
w
∣
∣
2
min||Xw−y||2+z||w||^2
min∣∣Xw−y∣∣2+z∣∣w∣∣2
这样的平方偏差因子向模型中引入了少量偏差,但大大减少了方差。
岭回归的特点:
- 岭回归的假设和最小平方回归相同,但是在最小平方回归的时候我们假设数据服从高斯分布使用的是极大似然估计(MLE),在岭回归的时候由于添加了偏差因子,即w的先验信息,使用的是极大后验估计(MAP)来得到最终的参数。极大似然估计和最大后验估计看这里
- 没有特征选择功能
4 Lasso回归
与岭回归类似,都是对损失函数后面加一个惩罚项,也就是正则化。岭回归采用的是L2正则,Lasso回归采用的是L1正则化,
m
i
n
∣
∣
X
w
−
y
∣
∣
2
+
Z
∣
∣
w
∣
∣
min||Xw−y||^2+Z||w||
min∣∣Xw−y∣∣2+Z∣∣w∣∣
L1正则化和L2正则化的详细讲解看这里:https://blog.csdn.net/jinping_shi/article/details/52433975 或者点击这里
L1范数倾向于产生稀疏系数,可以用来做参数选择,也叫特征选择。而L2正则化易产生非稀疏系数,所以不可以做特征选择,更多的就是用来防止过拟合。一定程度上,L1正则化也可以防止过度拟合。
稀疏性是指:很多元素都是0,只有极少数的非零元素。这样得到的大部分参数的系数都是0。
5 弹性回归网络
弹性回归网络是Lesso回归和岭回归技术的混合体。它使用了L1和L2正则化,也达到了两种技术共有的效果,弹性回归网络的表达式如下:
m
i
n
∣
∣
X
w
−
y
∣
∣
2
+
z
1
∣
∣
w
∣
∣
+
z
2
∣
∣
w
∣
∣
2
min||Xw−y||^2+z1||w||+z2||w||^2
min∣∣Xw−y∣∣2+z1∣∣w∣∣+z2∣∣w∣∣2
在Lasso和岭回归之间进行权衡的一个实际是运行弹性网络在循环的情况下继承岭回归的一些稳定性。
弹性回归网络的优点:
- 鼓励在高度相关变量的情况下的群体效应,而不像Lasso那样将其中一些置为0.当多个特征和另一个特征相关的时候弹性网络非常有用。Lasso倾向于随机选择其中一个,而弹性网络倾向于选择两个。
- 对所选变量的数量没有限制。
























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








