[CVPR 2022] Balanced Contrastive Learning for Long-Tailed Visual Recognition

Introduction

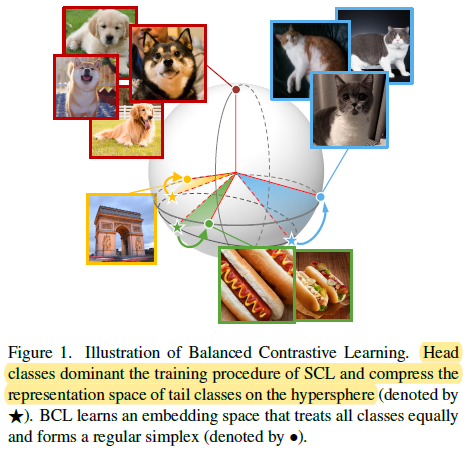
• 作者发现对于在长尾数据集上，Supervised contrastive loss 学得的特征并不能形成 regular simplex (which is an ideal geometric configuration for representation learning).
• 为了解决上述问题，让模型学得 balanced feature，作者提出了 balanced contrastive learning (BCL)，用 class-averaging 平衡负类的梯度贡献，用 class-complement 让所有类别都出现在每个 mini-batch 中。经过理论证明，BCL 可以使得特征满足 regular simplex
  

Method

Preliminaries

• Supervised contrastive loss
  其中，$z_i$ 为样本 $x_i$ 的特征表示并且 $||{\mathbf{z}}_{\mathbf{i}}|{|}_2=1$，$B_y$ 是一个 batch $B$ 里类别为 $y$ 的子集。由此可以定义 class-specific batch-wise loss
  
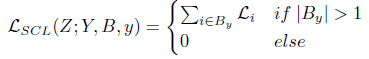
• Regular simplex：假设 regular simplex 嵌入在半径 $\rho >0$ 的超球中，它的 $K$ 个顶点为 ${\xi }_1,..,{\xi }_K\in {\mathbb{R}}^h$ ($K\le h+1$)，则该 regular simplex 的充要条件为
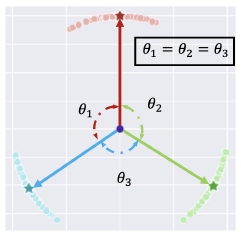
  可见，regular simplex 关于原点高度对称，并且各个顶点均匀分布在空间中。假如数据集为均衡数据集，则当 supervised contrastive loss 达到最小值时，各个类别的特征表示就会坍塌为 regular simplex 的各个顶点
  

Balanced Contrastive Learning (BCL)

Drawbacks of SCL

• 对于使用 supervised contrastive loss 的 class-specific batch-wise loss ${\mathcal{L}}_{SCL}(Z;Y,B,y)$，作者在定理 1 给出了其下界 (derived by Graf, Florian, et al. “Dissecting supervised constrastive learning.” International Conference on Machine Learning. PMLR, 2021.)：
  可见 SCL loss 的下界由 repulsion term $\frac{1}{|B_y^C|}{\sum }_{k\in B_y^C}{z}_i\cdot z_k$ 和 attraction term − 1 ∣ B y ∣ − 1 ∑ j ∈ B y \ { i } z i ⋅ z j -\frac{1}{|B_y|-1}\sum_{j \in B_y \backslash\{i\}} z_i \cdot z_j −∣By​∣−11​∑j∈By​\{i}​zi​⋅zj​ 组成
• attraction term − 1 ∣ B y ∣ − 1 ∑ j ∈ B y \ { i } z i ⋅ z j -\frac{1}{|B_y|-1}\sum_{j \in B_y \backslash\{i\}} z_i \cdot z_j −∣By​∣−11​∑j∈By​\{i}​zi​⋅zj​：The attraction term leads to intra-class feature collapse regardless of the class frequency. 随着训练的进行，attraction term 会导致 variability collapse (all the within-class representations collapse to their class means in the end) (Papyan, Vardan, X. Y. Han, and David L. Donoho. “Prevalence of neural collapse during the terminal phase of deep learning training.” Proceedings of the National Academy of Sciences 117.40 (2020): 24652-24663.). 同时注意到，attraction term 只与同类样本有关，因此数据集是否均衡并不会对 attraction term 产生影响 (但可能会导致类内特征学习不充分，类内样本特征不相似)，无论数据集怎样，类内样本都应该尽可能接近
• repulsion term $\frac{1}{|B_y^C|}{\sum }_{k\in B_y^C}{z}_i\cdot z_k$：repulsion term 影响的是 inter-class uniformity. 作者认为 data imbalance 主要影响的就是 repulsion term，这是因为当数据集长尾时，mini-batch 也是长尾的，这会导致 repulsion term 由多数类主导 (the gradients from negative head classes will be much larger than negative tail classes)，$z_i$ 会尽量远离多数类特征，但由于少数类样本很少，$z_i$ 并不会很彻底地和少数类特征分开，最终导致的结果就是多数类和其他类特征距离较远，但少数类和少数类之间特征距离较近，也就是形成了如下的非对称几何结构：
  

Proof:

• (1) 首先对 ${\mathcal{L}}_{SCL}(Z;Y,B,y)$ 做一点变换
  L S C L ( Z ; Y , B , y ) = ∑ i ∈ B y − 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } log ⁡ exp ⁡ ( z i ⋅ z p ) ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) = ∑ i ∈ B y 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } log ⁡ ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) exp ⁡ ( z i ⋅ z p ) = ∑ i ∈ B y 1 ∣ B y ∣ − 1 log ⁡ ( ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) ) ∣ B y ∣ − 1 ∏ p ∈ B y \ { i } exp ⁡ ( z i ⋅ z p ) = ∑ i ∈ B y log ⁡ ( ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) ∏ p ∈ B y \ { i } exp ⁡ ( z i ⋅ z p ) 1 / ∣ B y ∣ − 1 ) = ∑ i ∈ B y log ⁡ ( ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) \begin{aligned} \mathcal{L}_{S C L}(Z ; Y, B, y) &=\sum_{i \in B_y}-\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} \log \frac{\exp \left(z_i \cdot z_p\right)}{\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)} \\ &=\sum_{i \in B_y}\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} \log \frac{\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)}{\exp \left(z_i \cdot z_p\right)} \\ &=\sum_{i \in B_y}\frac{1}{\left|B_y\right|-1} \log \frac{(\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k))^{|B_y|-1}}{\prod_{p \in B_y \backslash\{i\}}\exp \left(z_i \cdot z_p\right)} \\ &=\sum_{i \in B_y} \log \left(\frac{\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)}{\prod_{p \in B_y \backslash\{i\}} \exp \left(z_i\cdot z_p\right)^{1 /\left|B_y\right|-1}}\right) \\ &=\sum_{i \in B_y} \log \left(\frac{\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)}{\exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)}\right) \end{aligned} LSCL​(Z;Y,B,y)​=i∈By​∑​−∣By​∣−11​p∈By​\{i}∑​log∑k∈B\{i}​exp(zi​⋅zk​)exp(zi​⋅zp​)​=i∈By​∑​∣By​∣−11​p∈By​\{i}∑​logexp(zi​⋅zp​)∑k∈B\{i}​exp(zi​⋅zk​)​=i∈By​∑​∣By​∣−11​log∏p∈By​\{i}​exp(zi​⋅zp​)(∑k∈B\{i}​exp(zi​⋅zk​))∣By​∣−1​=i∈By​∑​log ​∏p∈By​\{i}​exp(zi​⋅zp​)1/∣By​∣−1∑k∈B\{i}​exp(zi​⋅zk​)​ ​=i∈By​∑​log ​exp(∣By​∣−11​∑p∈By​\{i}​zi​⋅zp​)∑k∈B\{i}​exp(zi​⋅zk​)​ ​​
• (2) 然后尝试将 ${\mathcal{L}}_{SCL}(Z;Y,B,y)$ 的分子项拆成 repulsion term 和 attraction term. 先把分子项拆成 $z_i$ 和正类的相似度之和以及 $z_i$ 和负类的相似度之和两项：
  ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) = ∑ k ∈ B y \ { i } exp ⁡ ( z i ⋅ z k ) + ∑ k ∈ B j , j ≠ y exp ⁡ ( z i ⋅ z k ) \sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)=\sum_{k\in B_y\backslash \{i\}}\exp(z_i\cdot z_k)+\sum_{k\in B_j,j\neq y}\exp(z_i\cdot z_k) k∈B\{i}∑​exp(zi​⋅zk​)=k∈By​\{i}∑​exp(zi​⋅zk​)+k∈Bj​,j=y∑​exp(zi​⋅zk​)由 Jenson 不等式可知 (指数函数为凸函数)，
  ∑ k ∈ B y \ { i } exp ⁡ ( z i ⋅ z k ) ≥ ( Q 1 ) ( ∣ B y ∣ − 1 ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ k ∈ B y \ { i } z i ⋅ z k ) ∑ k ∈ B j , j ≠ y exp ⁡ ( z i ⋅ z k ) ≥ ( Q 2 ) ∣ B y C ∣ exp ⁡ ( 1 ∣ B y C ∣ ∑ k ∈ B j , j ≠ y z i ⋅ z k ) \sum_{k\in B_y\backslash \{i\}}\exp(z_i\cdot z_k) \stackrel{(Q 1)}{\geq}(|B_y|-1) \exp \left(\frac{1}{|B_y|-1} \sum_{k\in B_y\backslash \{i\}} z_i \cdot z_k\right)\\ \sum_{k\in B_j,j\neq y}\exp(z_i\cdot z_k) \stackrel{(Q 2)}{\geq}|B_y^C| \exp \left(\frac{1}{|B_y^C|} \sum_{k\in B_j,j\neq y} z_i \cdot z_k\right) k∈By​\{i}∑​exp(zi​⋅zk​)≥(Q1)​(∣By​∣−1)exp ​∣By​∣−11​k∈By​\{i}∑​zi​⋅zk​ ​k∈Bj​,j=y∑​exp(zi​⋅zk​)≥(Q2)​∣ByC​∣exp ​∣ByC​∣1​k∈Bj​,j=y∑​zi​⋅zk​ ​取等号时当且仅当
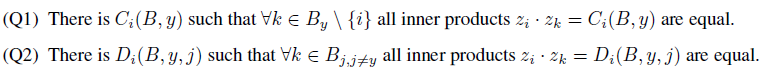  将上面两个不等式代入 ${\mathcal{L}}_{SCL}(Z;Y,B,y)$ 可以得到它的一个下界
  L S C L ( Z ; Y , B , y ) = ∑ i ∈ B y log ⁡ ( ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) ≥ ∑ i ∈ B y log ⁡ ( ( ∣ B y ∣ − 1 ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ k ∈ B y \ { i } z i ⋅ z k ) + ∣ B y C ∣ exp ⁡ ( 1 ∣ B y C ∣ ∑ k ∈ B j , j ≠ y z i ⋅ z k ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) = ∑ i ∈ B y log ⁡ ( ( ∣ B y ∣ − 1 ) + ∣ B y C ∣ exp ⁡ ( 1 ∣ B y C ∣ ∑ k ∈ B j , j ≠ y z i ⋅ z k − 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) \begin{aligned} \mathcal{L}_{S C L}(Z ; Y, B, y) &=\sum_{i \in B_y} \log \left(\frac{\sum_{k\in B\backslash \{i\}}\exp(z_i\cdot z_k)}{\exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)}\right) \\&\geq \sum_{i \in B_y} \log \left(\frac{(|B_y|-1) \exp \left(\frac{1}{|B_y|-1} \sum_{k\in B_y\backslash \{i\}} z_i \cdot z_k\right)+|B_y^C| \exp \left(\frac{1}{|B_y^C|} \sum_{k\in B_j,j\neq y} z_i \cdot z_k\right)}{\exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)}\right) \\&= \sum_{i \in B_y} \log \left((|B_y|-1)+|B_y^C| \exp \left(\frac{1}{|B_y^C|} \sum_{k\in B_j,j\neq y} z_i \cdot z_k-\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)\right) \end{aligned} LSCL​(Z;Y,B,y)​=i∈By​∑​log ​exp(∣By​∣−11​∑p∈By​\{i}​zi​⋅zp​)∑k∈B\{i}​exp(zi​⋅zk​)​ ​≥i∈By​∑​log ​exp(∣By​∣−11​∑p∈By​\{i}​zi​⋅zp​)(∣By​∣−1)exp(∣By​∣−11​∑k∈By​\{i}​zi​⋅zk​)+∣ByC​∣exp(∣ByC​∣1​∑k∈Bj​,j=y​zi​⋅zk​)​ ​=i∈By​∑​log ​(∣By​∣−1)+∣ByC​∣exp ​∣ByC​∣1​k∈Bj​,j=y∑​zi​⋅zk​−∣By​∣−11​p∈By​\{i}∑​zi​⋅zp​ ​ ​​取等号时当且仅当对每个 $i\in B_y$，都有 $Q_1$ 和 $Q_2$ 成立，其中 $C_i(B,y)$ 和 $D_i(B,y,j)$ 只依赖于 batch $B$ 和 label $y$

---

• 为了解决上述问题，作者提出了两个方法：class-averaging 和 class-complement，两者结合在一起就得到了 Balanced contrastive loss，它能使得对比学习在长尾数据集上也能学得 regular simplex 的特征几何结构。class-averaging 通过平衡 repulsion term 中不同负类的梯度贡献来避免 repulsion term 被多数类主导；class-complement 则是使得所有类别都出现在每个 mini-batch 内

Class-averaging

• 平衡 repulsion term 中不同负类的梯度贡献最简单的方法就是减小分母项里的头部类别权重，可以有如下 3 种不同的损失形式：
  其中 ${\mathcal{L}}_1$ 和 ${\mathcal{L}}_2$ 唯一的区别就是平衡项 $\frac{1}{|B_j|}$ 位置不同，并且由 Jensen 不等式可知，${\mathcal{L}}_1\ge {\mathcal{L}}_2$. ${\mathcal{L}}_3$ 是 prototype-based contrastive learning

• 下面以 ${\mathcal{L}}_1$ 为例进行分析。相比 supervised contrastive loss，
  balanced contrastive loss 主要改变了 $\log$ 项的分母部分，将 ∑ k ∈ B \ { i } exp ⁡ ( z i ⋅ z k ) \sum_{k\in B\backslash\{i\}}\exp(z_i\cdot z_k) ∑k∈B\{i}​exp(zi​⋅zk​) 改成了 ${\sum }_{j\in {\mathcal{Y}}_B}\frac{1}{|B_j|}{\sum }_{k\in B_j}\exp (z_i\cdot z_k)$，其中 ${\mathcal{Y}}_B$ 为 batch $B$ 中包含的类别集合
  注意这里当 $j=y$，即类别为 $z_i$ 所属类别时，分母上的加和项实际为 1 ∣ B j ∣ − 1 ∑ k ∈ B j \ { i } exp ⁡ ( z i ⋅ z k ) \frac{1}{|B_j|-1}\sum_{k\in B_j\backslash \{i\}}\exp(z_i\cdot z_k) ∣Bj​∣−11​∑k∈Bj​\{i}​exp(zi​⋅zk​)，也就是说分母项实际上为 1 ∣ B y ∣ − 1 ∑ k ∈ B y \ { i } exp ⁡ ( z i ⋅ z k ) + ∑ j ∈ Y B , j ≠ y 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) \frac{1}{|B_y|-1}\sum_{k\in B_y\backslash \{i\}}\exp(z_i\cdot z_k)+\sum_{j\in\mathcal Y_B,j\neq y}\frac{1}{|B_j|}\sum_{k\in B_j}\exp(z_i\cdot z_k) ∣By​∣−11​∑k∈By​\{i}​exp(zi​⋅zk​)+∑j∈YB​,j=y​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)，这里为了书写方便写成了论文中的形式

• 对于使用 balanced contrastive loss 的 class-specific batch-wise loss ${\mathcal{L}}_{BCL}(Z;Y,B,y)$，作者在定理 2 给出了其下界：
  

• attraction term − 1 ∣ B y ∣ − 1 ∑ j ∈ B y \ { i } z i ⋅ z j -\frac{1}{|B_y|-1}\sum_{j \in B_y \backslash\{i\}} z_i \cdot z_j −∣By​∣−11​∑j∈By​\{i}​zi​⋅zj​：和 supervised contrastive loss 对应的 attraction term 相同

• repulsion term 1 ∣ Y B ∣ − 1 ∑ q ∈ Y B \ { y } 1 ∣ B q ∣ ∑ k ∈ B q z i ⋅ z k \frac{1}{|\mathcal Y_B|-1}\sum_{q\in \mathcal Y_B\backslash\{y\}}\frac{1}{|B_q|}\sum_{k\in B_q} z_i \cdot z_k ∣YB​∣−11​∑q∈YB​\{y}​∣Bq​∣1​∑k∈Bq​​zi​⋅zk​：相比 supervised contrastive loss 对应的 attraction term $\frac{1}{|B_y^C|}{\sum }_{k\in B_y^C}{z}_i\cdot z_k$，balanced contrastive loss 按照类别给 $z_i\cdot z_k$ 做了加权，多数类不再主导 repulsion term，每个类别对梯度的贡献都相同

Proof.

• (1) 首先对 ${\mathcal{L}}_{BCL}(Z;Y,B,y)$ 做一点变换
  L B C L ( Z ; Y , B , y ) = ∑ i ∈ B y − 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } log ⁡ exp ⁡ ( z i ⋅ z p ) ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) = ∑ i ∈ B y 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } log ⁡ ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) exp ⁡ ( z i ⋅ z p ) = ∑ i ∈ B y 1 ∣ B y ∣ − 1 log ⁡ ( ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) ) ∣ B y ∣ − 1 ∏ p ∈ B y \ { i } exp ⁡ ( z i ⋅ z p ) = ∑ i ∈ B y log ⁡ ( ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) ∏ p ∈ B y \ { i } exp ⁡ ( z i ⋅ z p ) 1 / ∣ B y ∣ − 1 ) = ∑ i ∈ B y log ⁡ ( ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) \begin{aligned} \mathcal{L}_{B C L}(Z ; Y, B, y) &=\sum_{i \in B_y}-\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} \log \frac{\exp \left(z_i \cdot z_p\right)}{\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right)} \\ &=\sum_{i \in B_y}\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} \log \frac{\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right)}{\exp \left(z_i \cdot z_p\right)} \\ &=\sum_{i \in B_y}\frac{1}{\left|B_y\right|-1} \log \frac{(\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right))^{|B_y|-1}}{\prod_{p \in B_y \backslash\{i\}}\exp \left(z_i \cdot z_p\right)} \\ &=\sum_{i \in B_y} \log \left(\frac{\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right)}{\prod_{p \in B_y \backslash\{i\}} \exp \left(z_i\cdot z_p\right)^{1 /\left|B_y\right|-1}}\right) \\ &=\sum_{i \in B_y} \log \left(\frac{\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right)}{\exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)}\right) \end{aligned} LBCL​(Z;Y,B,y)​=i∈By​∑​−∣By​∣−11​p∈By​\{i}∑​log∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)exp(zi​⋅zp​)​=i∈By​∑​∣By​∣−11​p∈By​\{i}∑​logexp(zi​⋅zp​)∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)​=i∈By​∑​∣By​∣−11​log∏p∈By​\{i}​exp(zi​⋅zp​)(∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​))∣By​∣−1​=i∈By​∑​log ​∏p∈By​\{i}​exp(zi​⋅zp​)1/∣By​∣−1∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)​ ​=i∈By​∑​log ​exp(∣By​∣−11​∑p∈By​\{i}​zi​⋅zp​)∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)​ ​​
• (2) 然后尝试将 ${\mathcal{L}}_{BCL}(Z;Y,B,y)$ 的分子项拆成 repulsion term 和 attraction term (分子项实际上为 1 ∣ B y ∣ − 1 ∑ k ∈ B y \ { i } exp ⁡ ( z i ⋅ z k ) + ∑ j ∈ Y B , j ≠ y 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) \frac{1}{|B_y|-1}\sum_{k\in B_y\backslash \{i\}}\exp(z_i\cdot z_k)+\sum_{j\in\mathcal Y_B,j\neq y}\frac{1}{|B_j|}\sum_{k\in B_j}\exp(z_i\cdot z_k) ∣By​∣−11​∑k∈By​\{i}​exp(zi​⋅zk​)+∑j∈YB​,j=y​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)). 首先由 Jenson 不等式可知 (指数函数为凸函数)，
  取等号时当且仅当
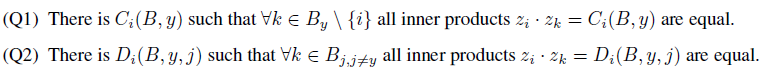  将上面两个不等式代入分子项可以得到分子项的一个下界
  在后面一项上继续套用 Jensen 不等式可知
  取等号时当且仅当 (注意到 $Q_3$ 和 $Q_2$ 其实是等价的)
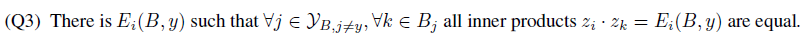  将上面不等式代入分子项可以得到其新的下界 (这个下界里的第一项其实就是 ${\mathcal{L}}_{BCL}(Z;Y,B,y)$ 中的分母项)
  ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) ≥ exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) + ( ∣ Y B ∣ − 1 ) exp ⁡ ( 1 ∣ Y B ∣ − 1 ∑ j ∈ Y B j ≠ y 1 ∣ B j ∣ ∑ k ∈ B j z i ⋅ z k ) \sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{\mathrm{k} \in B_j} \exp \left(z_i \cdot z_k\right) \geq \exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)+\left(\left|\mathcal{Y}_B\right|-1\right) \exp \left(\frac{1}{\left|\mathcal{Y}_B\right|-1} \sum_{\substack{j \in \mathcal{Y}_B \\ j \neq y}} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} z_i \cdot z_k\right) j∈YB​∑​∣Bj​∣1​k∈Bj​∑​exp(zi​⋅zk​)≥exp ​∣By​∣−11​p∈By​\{i}∑​zi​⋅zp​ ​+(∣YB​∣−1)exp ​∣YB​∣−11​j∈YB​j=y​∑​∣Bj​∣1​k∈Bj​∑​zi​⋅zk​ ​将其代入 ${\mathcal{L}}_{BCL}(Z;Y,B,y)$ 即可得到 1 个 batch 中 class-specific batch-wise loss 的下界
  L B C L ( Z ; Y , B , y ) = ∑ i ∈ B y log ⁡ ( ∑ j ∈ Y B 1 ∣ B j ∣ ∑ k ∈ B j exp ⁡ ( z i ⋅ z k ) exp ⁡ ( 1 ∣ B y ∣ − 1 ∑ p ∈ B y \ { i } z i ⋅ z p ) ) \begin{aligned} \mathcal{L}_{B C L}(Z ; Y, B, y) &=\sum_{i \in B_y} \log \left(\frac{\sum_{j \in \mathcal{Y}_B} \frac{1}{\left|B_j\right|} \sum_{k \in B_j} \exp \left(z_i \cdot z_k\right)}{\exp \left(\frac{1}{\left|B_y\right|-1} \sum_{p \in B_y \backslash\{i\}} z_i \cdot z_p\right)}\right) \end{aligned} LBCL​(Z;Y,B,y)​=i∈By​∑​log ​exp(∣By​∣−11​∑p∈By​\{i}​zi​⋅zp​)∑j∈YB​​∣Bj​∣1​∑k∈Bj​​exp(zi​⋅zk​)​ ​​取等号时当且仅当对每个 $i\in B_y$，都有 $Q_1$ 和 $Q_3$ 成立，其中 $C_i(B,y)$ 和 $E_i(B,y)$ 只依赖于 batch $B$ 和 label $y$
  

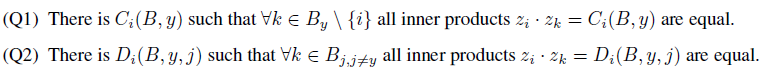
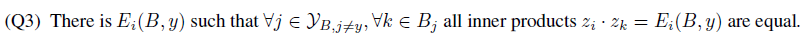
Class-complement

• Since each class is not sampled with equal probability, this may still lead to an unstable optimization and fail to form a regular simplex. To address this problem, we make all classes appear in every mini-batch and name this operation as class-complement
• 具体而言，作者引入了 class-center representations, i.e. prototypes for balanced contrastive learning (给一个 batch 里类别 $i\in \mathcal{Y}$ 的样本集加上类别 $i$ 的 class-center representation $c_i$). 原来的损失函数为
  加入 class-center representations 后就得到了最终的 balanced contrastive loss
  其中，class-center representation $c_i$ 是由 classifier weights 经过 FC 后得到 (the weights of the linear classifier are co-linear with these simplex vertices to which the classes collapse)
  

Lower bound of BCL

• 作者依然通过求损失函数下界的方式对 Class-complement 的作用进行了理论分析。作者在定理 3 中给出了使用 Class-complement 后的损失下界，该下界为一个 class-independent constant，并且当且仅当类特征满足 regular simplex structure 时取得损失下界：
  

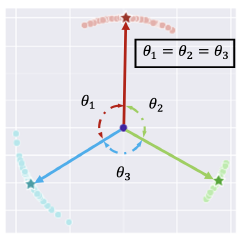
Proof

• (1) 首先进一步推得 BCL 损失的一个下界。由 Class-complement 可知，${\mathcal{Y}}_B=\mathcal{Y}$，因此 attraction term − 1 ∣ B y ∣ − 1 ∑ j ∈ B y \ { i } z i ⋅ z j -\frac{1}{|B_y|-1}\sum_{j \in B_y \backslash\{i\}} z_i \cdot z_j −∣By​∣−11​∑j∈By​\{i}​zi​⋅zj​ 和 repulsion term 1 ∣ Y B ∣ − 1 ∑ q ∈ Y B \ { y } 1 ∣ B q ∣ ∑ k ∈ B q z i ⋅ z k \frac{1}{|\mathcal Y_B|-1}\sum_{q\in \mathcal Y_B\backslash\{y\}}\frac{1}{|B_q|}\sum_{k\in B_q} z_i \cdot z_k ∣YB​∣−11​∑q∈YB​\{y}​∣Bq​∣1​∑k∈Bq​​zi​⋅zk​ 可以表示为
  之前求出的 BCL 损失下界可以写为
  其中 $S(Z;Y,B,y)$ 为 attraction term 和 repulsion term 之和
  由于 $f(x)=\log (1+\alpha \exp (x))$ ($\alpha >0$) 二阶连续可导且为凸函数，因此可以用 Jensen 不等式进一步给出其下界：
  $${\mathcal{L}}_{BCL}(Z;Y)\stackrel{(Q4)}{\ge }|\mathcal{D}|\log \left(1+(|\mathcal{Y}|-1)\exp \left(\frac{1}{|\mathcal{D}|}\sum _{B\in \mathcal{B}}\sum _{y\in \mathcal{Y}}\sum _{i\in B_y}S(Z;Y,B,y)\right)\right)$$取等号时当且仅当对 $\forall B\in \mathcal{B},\forall y\in \mathcal{Y},\forall i\in B_y$，都有 $Q_4$ 成立
  
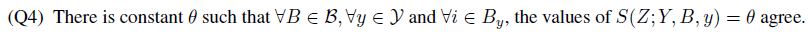
• (2) 下面考虑发生 variability collapse，也就是 attraction term 取得最小值的情况 ($||z_i||=1$)
  取等号时 (i.e. variability collapse) 当且仅当 $z_i,z_j$ 间的夹角余弦为 0，即 $Q_5$ 成立 (i.e. 属于类别 $i$ 的样本特征 $z_i$ 坍塌为类特征均值 $z_{c_i}$)
  此时将上述条件代入 BCL 损失函数的定义式可以得到
  L B C L = ∑ B ∈ B ∑ y ∈ Y ∑ i ∈ B y L i L i = − 1 ∣ B y ∣ ∑ p ∈ { B y \ { i } } ∪ { c y } log ⁡ exp ⁡ ( z i ⋅ z p ) 1 ∣ B y ∣ ∑ k ∈ { B y \ { i } } ∪ { c y } exp ⁡ ( z i ⋅ z k ) + ∑ j ∈ Y \ { y } 1 ∣ B j ∣ + 1 ∑ k ∈ B j ∪ { c j } exp ⁡ ( z i ⋅ z k ) = − 1 ∣ B y ∣ ∑ p ∈ { B y \ { i } } ∪ { c y } log ⁡ exp ⁡ ( z i ⋅ z c y ) exp ⁡ ( z i ⋅ z c y ) + ∑ j ∈ Y \ { y } exp ⁡ ( z i ⋅ z c j ) = − log ⁡ exp ⁡ ( z i ⋅ z c y ) exp ⁡ ( z i ⋅ z c y ) + ∑ j ∈ Y \ { y } exp ⁡ ( z i ⋅ z c j ) \begin{aligned} \mathcal{L}_{B C L} &=\sum_{B \in \mathcal{B}} \sum_{y \in \mathcal{Y}} \sum_{i \in B_y} \mathcal{L}_i \\ \mathcal{L}_i &= -\frac{1}{\left|B_y\right|} \sum_{p \in \{B_y \backslash\{i\}\}\cup\{c_y\}} \log \frac{\exp \left(z_i \cdot z_p\right)}{\frac{1}{\left|B_y\right|} \sum_{k \in \{B_y \backslash\{i\}\}\cup\{c_y\}} \exp \left(z_i \cdot z_k\right)+\sum_{j \in \mathcal{Y}\backslash\{y\}} \frac{1}{\left|B_j\right|+1} \sum_{k \in B_j\cup\{c_j\}} \exp \left(z_i \cdot z_k\right)} \\&= -\frac{1}{\left|B_y\right|} \sum_{p \in \{B_y \backslash\{i\}\}\cup\{c_y\}} \log \frac{\exp \left(z_i \cdot z_{c_y}\right)}{\exp \left(z_i \cdot z_{c_y}\right)+\sum_{j \in \mathcal{Y}\backslash\{y\}} \exp \left(z_i \cdot z_{c_j}\right)} \\&=-\log \frac{\exp \left(z_i \cdot z_{c_y}\right)}{\exp \left(z_i \cdot z_{c_y}\right)+\sum_{j \in \mathcal{Y} \backslash\{y\}} \exp \left(z_i \cdot z_{c_j}\right)} \end{aligned} LBCL​Li​​=B∈B∑​y∈Y∑​i∈By​∑​Li​=−∣By​∣1​p∈{By​\{i}}∪{cy​}∑​log∣By​∣1​∑k∈{By​\{i}}∪{cy​}​exp(zi​⋅zk​)+∑j∈Y\{y}​∣Bj​∣+11​∑k∈Bj​∪{cj​}​exp(zi​⋅zk​)exp(zi​⋅zp​)​=−∣By​∣1​p∈{By​\{i}}∪{cy​}∑​logexp(zi​⋅zcy​​)+∑j∈Y\{y}​exp(zi​⋅zcj​​)exp(zi​⋅zcy​​)​=−logexp(zi​⋅zcy​​)+∑j∈Y\{y}​exp(zi​⋅zcj​​)exp(zi​⋅zcy​​)​​相当于是 $z_i$ 在和所有类别的聚类中心做对比损失，这个损失是均衡的，并且它对应的最优解一定满足 simplex configuration
• (3) 利用 (1) 和 (2) 的结论可以推出 variability collapse 时 BCL 损失的下界。由 $Q_4$ 可知，
  $${\mathcal{L}}_{BCL}(Z;Y)\stackrel{(Q4)}{\ge }|\mathcal{D}|\log \left(1+(|\mathcal{Y}|-1)\exp \left(S(Z;Y,B,y)\right)\right)$$下面重点求 $S(Z;Y,B,y)$
  S ( Z ; Y , B , y ) = − 1 ∣ B y ∣ − 1 ∑ j ∈ B y \ { i } z i ⋅ z j + 1 ∣ Y ∣ − 1 ∑ q ∈ Y \ { y } 1 ∣ B q ∣ ∑ k ∈ B q z i ⋅ z k = − 1 + 1 ∣ Y ∣ − 1 ∑ q ∈ Y \ { y } 1 ∣ B q ∣ ∑ k ∈ B q z i ⋅ z c q = − 1 + 1 ∣ Y ∣ − 1 ∑ q ∈ Y \ { y } z i ⋅ z c q \begin{aligned} S(Z ; Y, B, y)&=-\frac{1}{\left|B_y\right|-1} \sum_{j \in B_y \backslash\{i\}} z_i \cdot z_j +\frac{1}{|\mathcal{Y}|-1} \sum_{q \in \mathcal{Y} \backslash\{y\}} \frac{1}{\left|B_q\right|} \sum_{k \in B_q} z_i \cdot z_k \\&=-1+\frac{1}{|\mathcal{Y}|-1} \sum_{q \in \mathcal{Y} \backslash\{y\}} \frac{1}{\left|B_q\right|} \sum_{k \in B_q} z_i \cdot z_{c_q} \\&=-1+\frac{1}{|\mathcal{Y}|-1} \sum_{q \in \mathcal{Y} \backslash\{y\}} z_i \cdot z_{c_q} \end{aligned} S(Z;Y,B,y)​=−∣By​∣−11​j∈By​\{i}∑​zi​⋅zj​+∣Y∣−11​q∈Y\{y}∑​∣Bq​∣1​k∈Bq​∑​zi​⋅zk​=−1+∣Y∣−11​q∈Y\{y}∑​∣Bq​∣1​k∈Bq​∑​zi​⋅zcq​​=−1+∣Y∣−11​q∈Y\{y}∑​zi​⋅zcq​​​回忆一下 regular simplex 的定义 (variability collapse 时 $z_{c_i}$ 即为 regular simplex 的顶点 ${\xi }_i$)
  将条件 (1) 代入 $S(Z;Y,B,y)$ 可得
  $$\begin{array}{rl}S(Z;Y,B,y)& =-1+\frac{1}{|\mathcal{Y}|-1}(-z_i\cdot z_{c_y})\\ & =-1-\frac{1}{|\mathcal{Y}|-1}\\ & =-\frac{|\mathcal{Y}|}{|\mathcal{Y}|-1}\end{array}$$因此有
  $$\begin{array}{rl}{\mathcal{L}}_{BCL}(Z;Y)& \stackrel{(Q4)}{\ge }|\mathcal{D}|\log \left(1+(|\mathcal{Y}|-1)\exp \left(S(Z;Y,B,y)\right)\right)\\ & =|\mathcal{D}|\log \left(1+(|\mathcal{Y}|-1)\exp \left(-\frac{|\mathcal{Y}|}{|\mathcal{Y}|-1}\right)\right)\end{array}$$也就是说，此时 BCL 损失的下界是一个常数。取等号时当且仅当
  

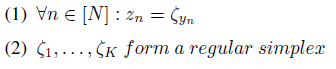
Gradient Analysis

• Khosla, Prannay, et al. “Supervised contrastive learning.” Advances in Neural Information Processing Systems 33 (2020): 18661-18673. 中给出了 SCL 的梯度公式 (这里省略温度系数 $\tau$)：
  其中，$w_i$ 为 unnormalized output，i.e., $z_i=w_i/\Vert w_i\Vert$
  下面主要考虑负样本带来的梯度贡献，即 negative term
• 对于 BCL，同样可以推导出梯度公式为
  其中，
  与 SCL 对比可以看出，首先 BCL 平衡了负样本带来的梯度 (i.e., negative term)，避免了头部类负样本带来的 tremendous gradient update. 同时，BCL 还平衡了正样本带来的梯度 (i.e., positive term)，尾部类的正样本能够提供更大的梯度，使得尾部类的同类样本更紧密地聚合在一起，相比 SCL 具有更好的 feature alignment 能力

同时它也保持了 SCL 具备的 implicit hard positive/negative example mining 的特点

Optimization with Logit Compensation

• 针对长尾数据集训练集、测试集分布不同的情况，作者还加入了 Logit Compensation
  其中，${\alpha }_y=1,{\delta }_y=\log {\mathbb{P}}_y$，${\mathbb{P}}_y$ 为 label $y$ 的 class prior

Framework

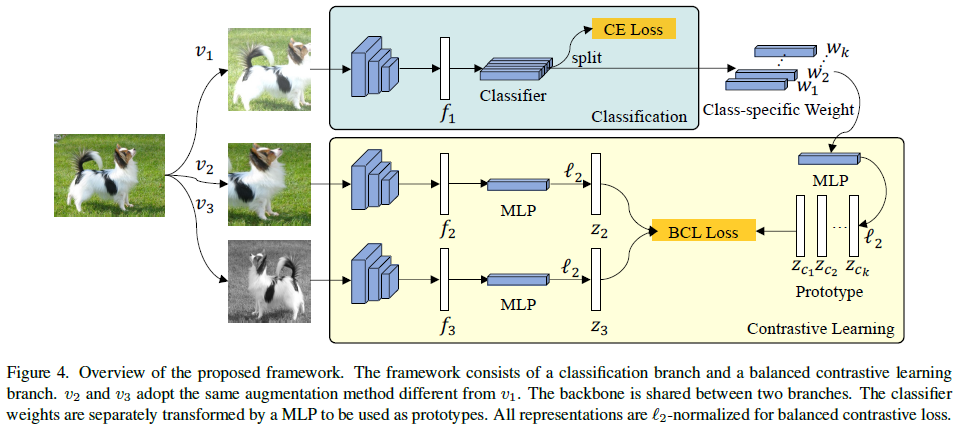
• framework (one stage training) 由 classification branch 和 balanced contrastive learning branch 组成，它们同时训练且共享 feature extractor. $v_1,v_2,v_3$ 均为数据增强后的图像，其中 $v_1$ 用于分类，$v_2,v_3$ 用于对比学习的 pairwise views ($v_2,v_3$ adopt the same augmentation method different from $v_1$). 对比学习分支通过 2 层 MLP 由 $f_i$ 得到 $z_i$
• 损失函数为
  前者是为了学得 balanced classifier，后者是为了学得 balanced feature (很多 2 stage 方法都忽略了对 balanced feature 的学习)

Experiment

• Long-tailed CIFAR (ResNet-32)：It’s worthwhile to mention that different to most of the pre-vious methods which compromise the performance of the head classes, our BCL further improves the performance of the head classes while simultaneously improving the tails.
  
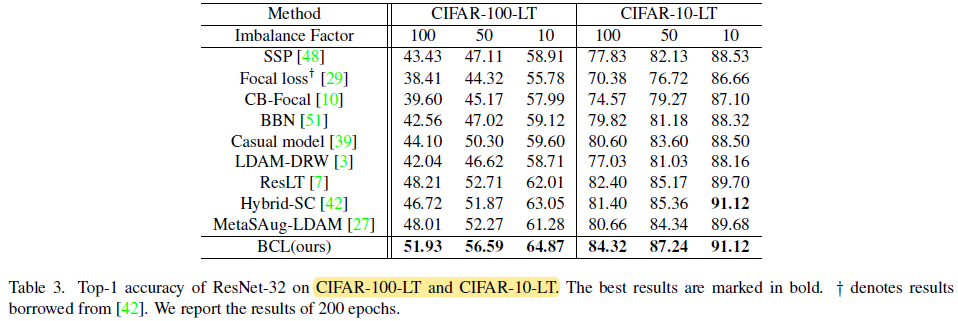
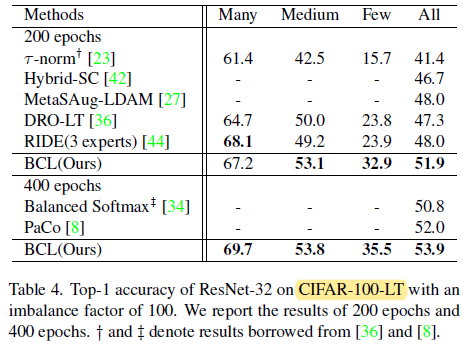
• ImageNet-LT and iNaturalist 2018
  

---

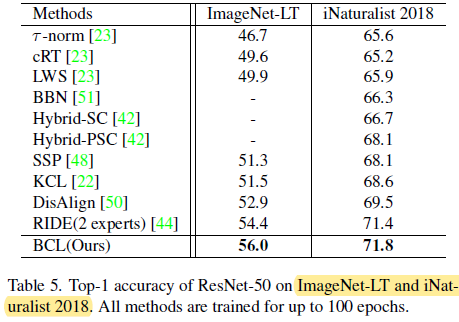
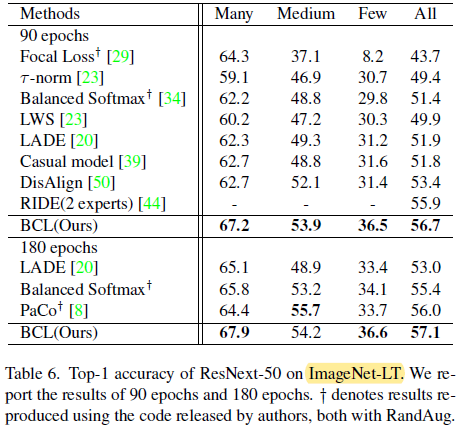
Ablation study (on CIFAR-100 with an imbalance factor of 100)

• different class-averaging implementations (i.e., ${\mathcal{L}}_1$, ${\mathcal{L}}_2$ and ${\mathcal{L}}_3$) (For ${\mathcal{L}}_3$, we use the prototype implemented in our work instead of the average of all embeddings of the same class.)
  
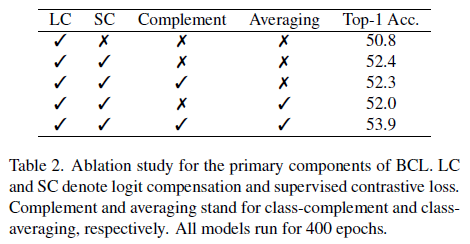
• Ablation study for the primary components of BCL：class complement 和 class averaging 要一起使用才能增强性能
  
• Ablations of Different Forms of Prototypes. We compare our method with the other two implementations of the prototype. The first one is using the exponential moving average to calculate the prototype. The second one is using learnable parameters [1, 5].
  
• Ablations of Different Configurations of Views. We compare our configuration with the other two configurations of views. We use the simple augmentation method, i.e., SimAug, to generate both views for contrastive learning. We further have one of the views generated via a stronger augmentation method, i.e., RandAug, or both of the views generated by RandAug. As shown in Table 2, stronger argumentation yields better performance.
  

References

• Zhu, Jianggang, et al. “Balanced Contrastive Learning for Long-Tailed Visual Recognition.” Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2022.
• code: https://github.com/FlamieZhu/Balanced-Contrastive-Learning