线段中点到另一直线距离最短_直线、射线和线段

一．概念描述

现代数学：在欧几里得几何学中，直线是几何学中的基本概念，是点在空间内沿相同或相反方向运动的轨迹。或者定义为：曲率最小的曲线(以无限长为半径的圆弧)。

射线亦称为半直线，是几何学的重要概念之一，指直线上任一点一旁的部分。这一点称为射线的端点。射线也可以定义为：从某一个确定的点出发，沿固定方向运动的点的轨迹。

线段是最基本的几何图形之一，界于两点间的直线部分称为线段这两点称为线段的端点。

初中数学对于直线、射线和线段的学习，也没有给出严格的定义，只是作为基本事实重点研究它们的特点。

小学数学：小学数学教材中没有对直线、射线和线段给出明确的定义，而是借助具体生活实例直观引导认识直线、射线和线段的特点。如2004年人教版教材四年级上册的第35页是这样描述射线的：像手电筒、汽车灯和太阳等射出来的光线，都可以近似地看成是射线。

二．概念解读

射线和线段的定义是在直线的基础上给出定义的，但直线涉及无限的概念，与长方体、正方体、长方形、正方形等相比，在现实中没有实物原型，这就需要通过想象逐步抽象、加深对直线的认识。相对于直线而言，射线虽然也涉及了无限的概念，但能够在生活中找到实物原型，如手电简照射出的光，因此认识要相对容易些。线段的认识要更容易一些，因为现实生活中有“线段”的实物原型，并且它是有限的、可测量的。

直线的特征：一是“直”的；二是可以向两方无限延伸；三是没有粗细之分。直线的表示方法一般有两种：如图1，记作直线L；如图2，记作直线AB或直线BA。

图1 图2

直线上的一点和它旁边的部分叫作射线，这个点叫作射线的端点。我们知道射线只有一个端点和一个方向，因此它也是不可度量的。在记录射线时，通常用射线上的端点和射线上任意一点来表示。如图3中的射线记作射线OA或射线L。

在记录射线时，要注意端点的顺序必须正确，比如射线OA不能表示成射线AO。同一条射线就是指射线的端点相同，而且延伸的方向也相同的射线。如图4，射线OA与射线OB表示同一条射线。两条端点相同、方向不同的射线，则是两条不同的射线。

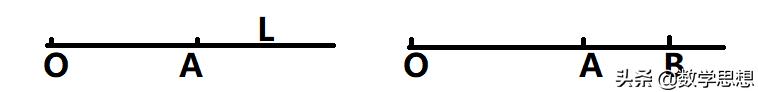
图3 图4

线段由于有两个端点，所以它的长度是有限的，可以测量的。而且在所有连接两点的线中，线段最短，即两点问的线段最短。线段也可以用表示它两个端点的字母或一个小写字母来表示，有时这些字母也表示线段长度。如图5记作线段AB或线段BA---注意线段AB和线段BA是同一条线段。如图6记作线段a。

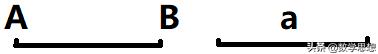
图5 图6

三．教学建议

小学阶段对于直线、射线和线段的学习，大多数教材都安排在一起，且基本都放在第二学段学习。但也有例外，如人教版教材是在二年级认识线段，在四年级把直线、射线与角的认识放在一起学习。虽然教材的编排顺序略有不同，但对于直线、射线和线段的学习，所有教材都是让学生在观察、对比中认识它们。因此，在教学中教师要注意以下几点。

(1)在具体的生活情境中认识线段、射线和直线

由于在现实中根本找不到“直线”的实物原型，射线和直线都涉及了无限的概念，所以在教学中，教师要结合具体的实例，并引导学生通过想象，认识直线和射线。对于线段的认识，由于现实生中有大量的实物原型，所以认识要容易一些，教师也可以在学生认识线段的

基础上，借助线段，通过想象进一步认识直线和射线。

如学生在认识线段后，教师拿出一个手电筒并打开它，让学生们随着手电简射出来的光束看，并引导说：“如果这束光线没有被阻挡，它将会怎样？”接着说：“在数学上也有这样的现象。想象一下，如果以一条线段的一个端点为端点，另一头无限延伸，会是怎样的一个图形呢？”

(2)在寻找直线、射线和线段间的区别与联系中进一步认识它们

教学中，教师要引导学生在不同中找相同、在相同中找不同，从而得到一些基本事实。基本事实是人们在长期实践中总结出来的结论。

(3)要在活动中初步感受直线、射线和线段的基本性质

对于直线、射线和线段的基本性质，教学中教师可以安排一些有意思的活动，让学生在活动中直观感受它们的性质。

例如，在学生认识直线、射线和线段后，我们可以尝试安排这样的活动：

①　用一个图钉把一张硬纸条钉在木板上，硬纸条可以转动吗？

②　用两个图钉把一张硬纸条钉在小板上，硬纸条可以转动吗？

通过这样的活动，引发学生的思考：过一点可以画出多少条直线？过两点可以画出多少条直线？在具体的活动中，帮助学生认识到：过一点能画无数条直线，过两点只能画一条直线。

四．推荐阅读

《数学辞海·第一卷》(裘光明，山西教育出版社，2002)

该书第118-120页从平面几何的角度对直线、射线、线段做了详细的解读。