树(Tree)——(五)搜索二叉树的节点删除和销毁

目录

节点删除的三种情况：

第一种情况：

第二种情况：

第三种情况

代码实现：

main函数

---

节点删除的三种情况：

节点删除总共分成三种情况：

第一种情况：

若为叶子节点则直接删除，如左图节点1，3 ，8或者右图的1，4，8。（若为单独一个根叶子要单独处理） 

若为单独一个根叶子

 

第二种情况：

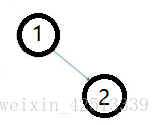
若该节点，有一个节点，左或是右。因为只有一个节点，直接令祖父节点指向孙子节点，孙子节点的左右需要分开判断。如图中节点2（若该节点为根要单独处理） 

 

若该节点为根

 

 

第三种情况

若该节点含有两个子节点，一般的删除策略是用其右子树的最小结点代替待删除结点的数据，然后递归删除那个右子树最小结点。即将第三种情况转化为第二种情况。如下图所示，要删除结点2，则找到结点2的右子树的最小结点3并将其数据赋值给结点2，然后在删除结点3。

第三种情况的特殊情况分析(删除的节点为2，右节点5没有左节点。则把节点2换成节点5) 

 

 

代码实现：

main函数

//这里没有用栈和队列，前面写的函数这次用到的，以用递归为主，不然代码太过冗余

#include <iostream>
#include<stdio.h>
#include<stdlib.h>
using namespace std;

struct TreeNode
{
    TreeNode*_left;
    TreeNode*_right;
    int _data;
};

void midOrderITraverse(TreeNode * r) //递归，中序，左根右
{
    if(r)
    {
        midOrderITraverse(r->_left);
        printf("%d ",r->_data);
        midOrderITraverse(r->_right);
    }
}

//递归版插入
void insertBstRecusive(TreeNode** root ,int data)
{
    if((*root) == NULL)
    {
        (*root) =(TreeNode*)malloc(sizeof(TreeNode));
        (*root)->_data =data;
        (*root)->_left = (*root)->_right =NULL;
    }
    else if(data > (*root)->_data)
    {
        insertBstRecusive(&((*root)->_right),data);
    }
    else
    {
        insertBstRecusive(&((*root)->_left),data);
    }
}

//查找，递归版
TreeNode* searchBstRecursive(TreeNode* r,int find)
{
    if(r)
    {
        if(r->_data == find)
            return r;
        else if(r->_data > find)
            return searchBstRecursive(r->_left,find);
        else
            return searchBstRecursive(r->_right,find);
    }
}

//寻找最小值、最大值
TreeNode* getMinBst(TreeNode* r)
{
    if(r)
    {
        while(r->_left)
        {
            r=r->_left;
        }
        return r;
    }
    return NULL;
}
TreeNode* getMaxBst(TreeNode* r)
{
    if(r)
    {
        while(r->_right)
            r=r->_right;
        return r;
    }
    return NULL;
}

//查找父节点,迭代版
TreeNode* getParentBst(TreeNode*r,TreeNode * child)
{
    static TreeNode*parent = NULL;
    if(r)
    {
        if(r->_right == child || r->_left ==child)
            parent =  r;
        getParentBst(r->_left,child);
        getParentBst(r->_right,child);
    }
    return parent;
}

//删除节点
void deleteBst(TreeNode** r,TreeNode * pDel)
{
    TreeNode* t = *r;
    TreeNode * parent = getParentBst(t,pDel);
    TreeNode * minRight; //找到右节点为树的最小节点
    if(*r == NULL || pDel == NULL)
        return ;
    if(pDel->_left == NULL && pDel->_right == NULL) //第一种情况
    {
        if(*r == pDel)  //若删除的节点为根
        {
            free(t);
            *r = NULL;
            return;
        }
        if(parent->_left == pDel)
            parent->_left = NULL;
        else
            parent->_right = NULL;
        free(pDel);
        return;
    }
    else if(pDel->_left !=NULL && pDel->_right == NULL)//第二种
    {
        if(*r == pDel)
        {
            *r = pDel->_left; //这里 *r , t , pDel的_left 都可以
            free(pDel);
            return;
        }
        if(parent->_left == pDel)
            parent->_left = pDel->_left;
        else
            parent->_right = pDel->_left;
        free(pDel);
        return;
    }
    else if(pDel->_left == NULL && pDel->_right != NULL)//第二种
    {
        if(*r == pDel)
        {
            *r = pDel->_right;
            free(pDel);
            return;
        }
        if(parent->_left == pDel)
            parent->_left = pDel->_right;
        else
            parent->_right = pDel->_right;
        free(pDel);
        return;
    }
    else
    {
        //这里不讨论删除节点是否为根的情况
        //因为无论删除的是不是根节点,左右节点不为空,都需要替换来删除
        minRight = getMinBst(pDel->_right);
        pDel->_data = minRight->_data;
        parent = getParentBst(t,minRight);

        if(minRight == pDel->_right)
            parent->_right = minRight->_right;  //这里pDel的_right无论是否为空都可以
        else
            parent->_left = minRight->_right;
        free(minRight);
    }
}

//销毁树
void destroyBst(TreeNode* r)
{
    if(r)
    {
        destroyBst(r->_left);
        destroyBst(r->_right);
        free(r);
    }
}

int main()
{
     TreeNode *root=NULL;            //树的初始化
     insertBstRecusive(&root,30);     //利用例子建造树
     insertBstRecusive(&root,8);
     insertBstRecusive(&root,15);
     insertBstRecusive(&root,36);
     insertBstRecusive(&root,100);
     insertBstRecusive(&root,32);

     midOrderITraverse(root);
     putchar(10);
     TreeNode * ch = searchBstRecursive(root,36);
     if(ch == NULL)
         printf("no find");
     else
         cout<<ch->_data<<" ,find it"<<endl;

    deleteBst(&root,ch);
    midOrderITraverse(root);

    if(root == NULL)
        printf("Tree is empty");

    destroyBst(root);
    root = NULL; //main函数必须有，防止野指针
     return 0;
}