效用函数推导需求函数_微观经济学(4) 消费者理论: 效用最大化、需求

最新推荐文章于 2025-01-25 22:58:05 发布

赵北云

最新推荐文章于 2025-01-25 22:58:05 发布

阅读量1.1w

点赞数

文章标签：效用函数推导需求函数

本文链接：https://blog.csdn.net/weixin_42519126/article/details/112714061

版权

一、效用最大化问题、需求存在性条件

1.1 Def 预算约束、"偏好最大化"需求

设
上存在偏好

. 消费者的收入限制为

, 面对的价格

.

(1) Budget Bundle(预算约束):

(2)
, 称为
给定
的
"偏好最大化"需求/马歇尔需求(Marshallian Demand), 简称需求.
注意, 此时
为集值函数(Correspondence).

1.2 Def-Prop 效用最大化问题(UMP)

设
在

上可被效用函数

表示,

称为
Utility Maximization Problem.
则
, 即"偏好最大化"等价转化为
效用最大化.
证: 由效用
表示偏好

的定义可知:

1.3 Prop 需求集值函数: 零阶齐次

为零次齐次函数:

证: 显然由于
是零次齐次的，根本没有改变UMP.

1.4 Prop 需求存在条件: 连续偏好(Weierstrass Theorem)

设
在

上连续. 则存在连续效用函数

表示

.

首先证明
的
紧性：
(1) 显然

有界, 因为
no goods is free;

(2)
为
闭集: 任取
. 由于

利用欧氏空间点列极限保号性:

.
Weierstrass Theorem:
由于
在

上连续，给定

,

在

上连续. 由于

为紧集，则有最值定理知: 存在

，即最优值存在且为单点, 最值集必然闭. 则再由

的连续性，其逆像

也为闭集. 又由于紧集闭子集也紧，则利用

的紧性可知

也为紧集.

关于连续函数与紧集的性质参考数学分析相关部分:

全能菜王李金夕：4.4 连续函数的性质：紧、一致连续、连通、逆zhuanlan.zhihu.com

更强的性质可由
给出:

全能菜王李金夕：Hemicontinuity of Correspondence 对应的连续性zhuanlan.zhihu.com

二、效用最大化问题求解：必要条件、预算等式(NLS)、边际替代率(NLS、Inner Solution)

2.1 Thm UMP一般解必要条件：KKT 条件

此处，我们对UMP做出进一步限制: 要求
为连续可微.

列出拉格朗日:
.

若
则必满足KKT一阶条件, 即:
(1)
;

( FOC) (2)
.

( Complementary Slackness) (3)

( Original Conditions and Nonnegative Lagrangians)
详见:

全能菜王李金夕：最优化几何杂谈：Kuhn-Tucker定理、包络定理zhuanlan.zhihu.com

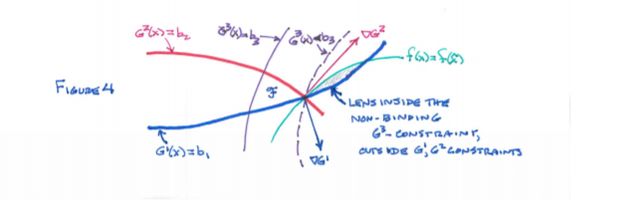
2.2 Prop "局部非餍足"的"连续"偏好: 需求必在预算线上(Walras' Law)

设
为
连续、 局部非餍足. 则
.

证: (反证法) 若
. 则记

. 考察平面

到点

的距离为

. 则记

,

到平面的距离为

. 则

.

显然由于局部非餍足
矛盾！

2.3 Def-Corollary UMP: "局部非餍足"偏好的"内点解"的必要条件

当
, 则称其为
内点解(Interior Solution相对于角解corner solution).
此时由松弛互补性，
.

再由局部非餍足偏好:
, 再由松弛互补性，

.

综上所述: 对于局部非餍足偏好的UMP内点解，即当
时, 必有:

(1)
(因为此时由内点解

)

(2)
且

.

3.3 Prop-Def 内点解: 边际替代率

商品 j 对商品 i 的边际替代率(Marginal Rate of Substitution of Good j for Good i):
. 则由3.3 (1)所述, 向量

与

平行，即

而
正是以商品

为计价单位计价的商品

的相对价格.
注意此结论仅限内点解.

三、效用最大化问题求解：充分条件

3.1 Prop 凸、严格凸的连续偏好(严格、拟凹效用函数): 需求为凸集、需求为单点

设
为连续、凸偏好, 则

为凸集. 设

为连续、严格凸偏好, 则

从集值函数退化成函数(单点).

证: 由上一节知: 连续偏好一定有连续效用函数表示；有效用函数表示的(严格)凸偏好其 效用函数一定为(严格)拟凹函数. 而 拟凹函数的最值集一定为凸集，详细证明见此文章:

全能菜王李金夕：最优化: Introduction of Quasi-Concavity & Convexityzhuanlan.zhihu.com

3.2 Thm UMP"局部非餍足""内点解"的充分条件：拟凹效用函数

设
为连续函数. 设

.

若
在点

处可微且

满足3.4 中的 KKT条件，即:

(1)

(2)

(3)
且

.

若
还为
拟凹函数(Quasiconcave), 则
为

参数下 UMP的全局解
.
证: (反证法)
设
. 则取

. 显然此时

. 可行性是由

的连续性保证: 考虑

的单变量函数

. 由于

为连续函数,

也为连续函数，则其复合函数

也为连续函数. 则由函数极限保号性:

则此时有
. 有

点的可微性，计算

而由拟凹函数的一阶充要条件知:
, 矛盾！拟凹函数性质详情参见

全能菜王李金夕：最优化: Introduction of Quasi-Concavity & Convexityzhuanlan.zhihu.com

四、间接效用函数、影子价格、罗伊恒等式

4.1 Def 间接效用函数

称UMP问题的最值函数
为间接效用函数(Indirect Utility Function).

即消费者面对

预算约束下可得到的最高效用.

4.2 Prop 间接效用函数性质

设连续效用函数
表示在

上的
局部非餍足偏好
. 则其UMP的

满足:

(1) Strictly increase in
; Decrease in

.

(2) Homogeneity of Degree 0:

(3) Quasiconvex in

(4) Continuous in
.

证：
(1) 取
. 由局部非餍足性得到 Walars' Law,

即由于
虽在

feasible，但

并未被取出作为需求.

同理, 取
. 由局部非餍足性得到 Walars' Law,

即由于

虽在

feasible，但

并未被取出作为需求.

(2) 由于预算约束
为零阶齐次，则显然成立.

(3) 由拟凸函数等价条件: 下等值集为凸集，只需证:
均为凸集. 取

.

.

若
矛盾！则WLOG设

(4)
的连续性由Berge's Maximum Theorem 给出, 略.

4.3 Thm 收入影子价格: Marginal Utility of Income

设对于UMP问题的需求(解)
退化为函数(不再是集值函数).

设
可微.

当
. 则UMP的拉格朗日乘数解即为预算约束条件的影子价格

证: 方法一: 包络定理：显然

方法二：由最值函数定义：
等式两边求

的偏导：

. 由前述性质，内点解满足

, 则

.

考察
两边对

求偏导，

, 代回即可.