效用函数推导需求函数_微观经济学笔记（4）需求

什么是“需求”？相信所有人都学过高中思想政治《经济生活》，一定还或多或少记得有一个向下倾斜的东西叫“需求曲线”，还记得需求曲线反人类地把自变量放到纵轴……可究竟什么是“需求”？

或许可以这样解释。我们观察一个某个商品的市场，当它的价格变化时，需求的数量也变化，这种函数关系就称为需求。没错。但大家有没有想过，为什么一定有一个“函数关系”？也就是说，为什么一定存在一个价格到商品数量的一一对应

？如果这不成立，是不是经济学的基础就不牢固了？再者，大家都默认了“需求曲线向下倾斜”，即所谓“需求定律”。这符合常理：价格越高，需求量就会下降。这真的成立吗？如果不成立，一些定律、模型是不是也就跟着失效了？这些问题促使我们更严谨地研究需求。

---

一、需求的存在性与唯一性

现代的需求理论是从个人的选择和需求出发的，将全体消费者的需求加总就得到了市场的需求。有人会说，这明显不靠谱呀！怎么可能得到所有消费者的选择，又怎么可能加总？实际上，现代理论不能帮我们得出需求的具体形式，但可以得出并解释需求的一些性质。只有基于这些性质，我们才能用其它方法建立方程（或许是计量经济学？我不太懂），再根据实际情况确定具体的需求曲线。从经济学研究的角度来说，现代需求理论是“理论”，具体得出需求的过程是“建模”，如何建模是需要理论来指导的。

之前的三篇笔记我们已经研究了消费者的预算约束、偏好和效用，现在我们来利用这些来得出消费者的需求。所谓个人的需求，就是给定了消费者的偏好结构，价格、预算确定的情况下使效用最大化的消费束。用数学语言就是：

这个优化问题的最优解：消费束

与价格向量

和预算

有关。那么向量函数

就称为需求函数。它是

的映射。

基于这个定义，我们再理解一下什么是需求。需求是一个优化问题的解！需求是一个优化问题的解！一旦价格和预算给定，消费者的消费就被约束了。在这个约束的条件下，消费者尽可能使效用最大，此时观测他的消费量，这个消费束就是在这个价格和预算下的需求。需求是理想（效用最大）与现实（预算约束）相妥协的解。

这么定义似乎很合理，但我们犯了一个数学上的错误。凭什么说一定存在这个“向量函数”？当你将一个问题的解定义成条件的函数时，需要证明解的存在性和唯一性。比如，我们知道函数极限的定义：若对于定义在

上的函数

，

，

，

，

，

，那么就称

在

处有极限，极限为

，并记为

.紧接着，我们就又给了它一个记号：

.这是不负责任的：除非我们说明上述定义的极限值

是唯一的，否则不能乱用等号。事实上，极限存在就唯一，这是很容易用反证法证明的。

这里也如此。我们需要证明两件事：这个优化问题的最优解存在且唯一。

解一定存在，证明如下：根据前面的约定，消费集

是闭集，且

，因此可行域

是有界闭区域。多元函数

是连续函数，在有界闭区域上连续的函数必有最大值。所以，最优解一定存在。□

在证明最优解唯一之前，我们先证明一个重要的结论：瓦尔拉斯法则。最优解

一定满足

.这说明消费者一定要用完所有的预算，这很好理解。证明如下：反证。假定

，根据局部非餍足性，必存在

，

且

，这与

是最优解矛盾。□

只要偏好关系是严格凸的，那么解一定唯一，证明如下：反证。假设存在

（

）都是最优化问题的解，那么

表示最大的效用，并且有

于是，

，

，也就是说

，同时根据严格凸性，

，则

，这说明可行域里有效用更高的消费束，矛盾！□

所以，如果偏好关系是严格凸的，就存在所说的需求函数

。它是

的映射。如果偏好关系不是严格凸的，那么最优解是一个集合，因此不存在这个映射。至此，我们解决了存在性与唯一性问题。下图（a）的偏好是凸的，但不是严格凸，这导致最优解是一个集合；图（b）的偏好是严格凸的。

---

二、需求函数的求解

现已给定理性的、连续的、单调的、严格凸的偏好结构

，即确定了效用函数

，那么如何求出需求函数

？这就是正式求解上文的规划问题。

在做数学推导之前，我们先从几何上分析。

几何上的分析

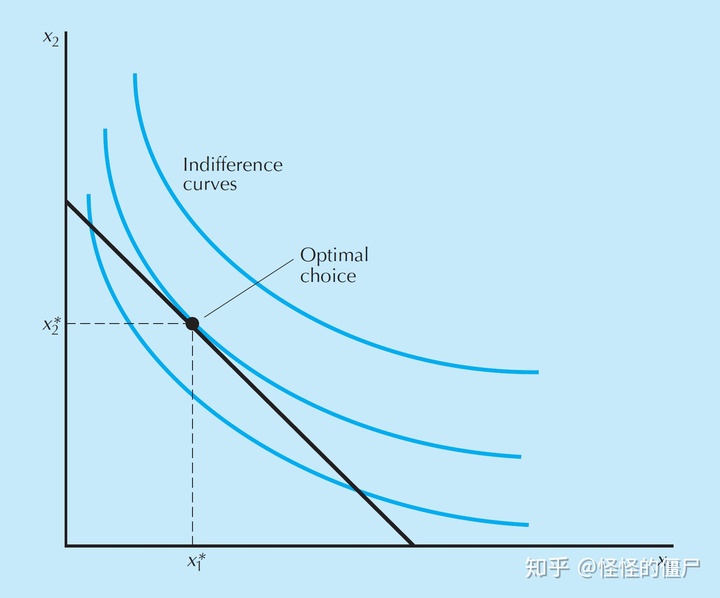
图中黑色的线段是预算线，在预算线以下的区域内，什么消费束的效用最大呢？我们考虑无差异曲线，每条无差异曲线对应一个效用

，当

增大时，无差异曲线向右上方移动，当无差异曲线与预算线相切时，效用达到最大。因为再往上移动，就不再满足预算约束；再向下移动，则效用不是最大。读者类比一下最简单的规划问题：高中数学的“线性规划”，那么这里的优化过程就很好理解了。

我们再做数学推导。在多元微积分中，我们学过多元连续函数求条件极值的方法：拉格朗日乘数法。我们来尝试使用。

拉格朗日函数

对每个变量求偏导，令偏导数等于零：

.

写成向量形式，即为

，等号左边是梯度。（注：下文不再用黑体。）

以上最优解满足的条件又被称为“一阶条件”。我们指出，

，因为根据单调性，梯度为正，价格也为正。

---

三、一阶条件的充分性

现在我们又遇到了几个问题。它们都是我们学习高数时就束手无策的问题：一阶条件一定可以求出极大值吗？一阶条件求出的一定是最大值吗？首先，我们回答第一个问题，答案是否定的，或者说又是拉格朗日乘数法得不出有意义的非负数解，这种情况被称为“角点解”。

角点解

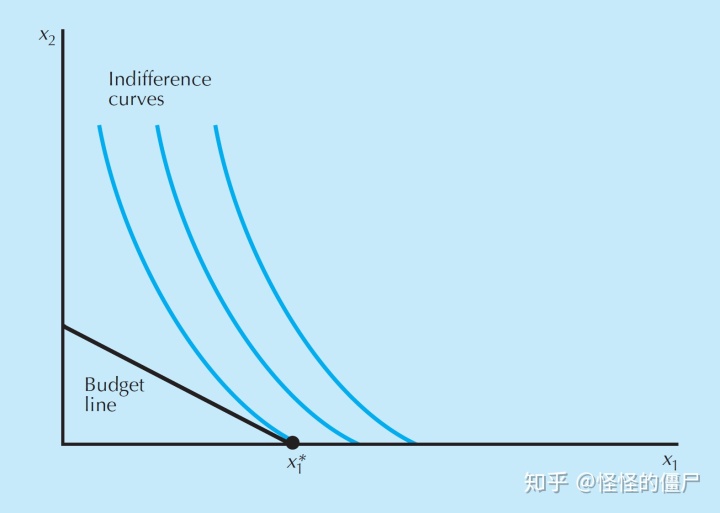
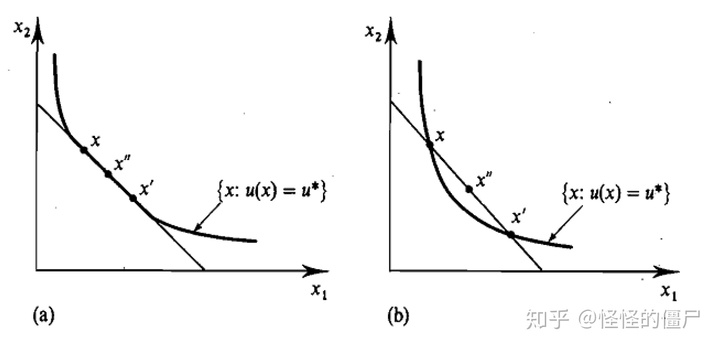
容易看出，上面的无差异曲线形状和预算线的斜率导致最优解处预算线并没有与无差异曲线相切，而是在某个坐标轴处相交。此时，如果非要求解一阶条件，很可能求出负数解。

高级微观经济学指出，库恩-塔克（Kuhn-Tucker）条件给出了更普遍适用的判别法。最优解

应同时满足：

从图形上看，它可以涵盖角点解的情形，如下图b。不再做过多解释。

第二个问题，答案是：只要解不是角点解，并且偏好是严格凸的，那么一阶条件确定的解一定是极大值，也是最大值。这对我们来说是很重要的。

在多元微积分中，极值问题还有二阶条件：若

满足一阶条件，Hessi矩阵：

负定，则

是极大值点。很遗憾，在这里我们不能证明Hessi矩阵一定是负定的。但是，关于条件极值问题有下述定理：

设函数

，满足等式约束

，若

满足一阶条件，且拉格朗日函数

的Hessi矩阵

在线性子空间

上半负定，则

是极大值点。

我么先来讨论一下严格凸的偏好满足什么数学条件。

偏好的严格凸性，等价于

，如果

且

，必有

. 从几何上可以这样考虑：

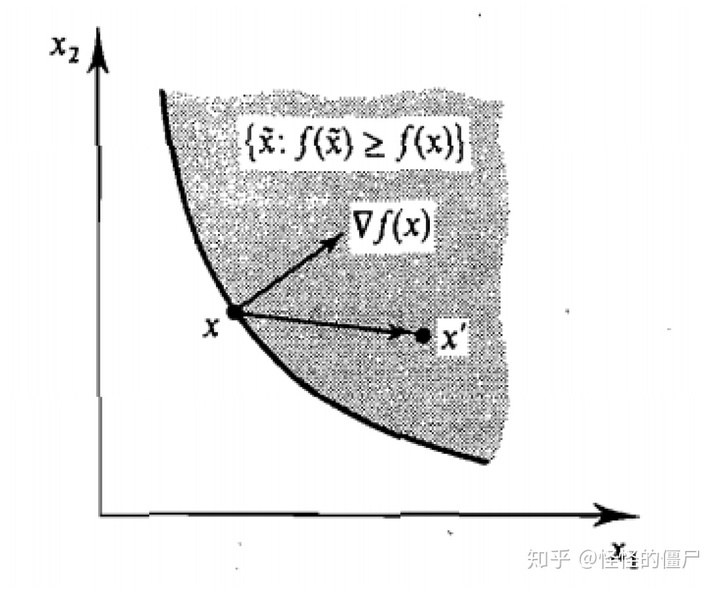
上图中，

。如果偏好严格凸，那么弱偏好集是严格凸集。

的弱偏好集内有某点

，连接两点的向量

一定与

处的梯度向量

成锐角。这很好理解，注意到

处的梯度一定垂直于无差异曲线。数学证明也很容易，需要用到凸集的定义，这里省略。（可耻地说一句“证 明 留 作 习 题”。)

注：此时效用函数

是“

拟凹函数”（quasi-concave function）。拟凹函数的定义是：若对于任意

，上轮廓集

是

凸集，则称函数是拟凹函数。若上轮廓集是严格凸集，则称函数是严格拟凹函数（strictly quasi-concave function）。满足凸性的偏好关系确定的效用函数是拟凹函数；满足严格凸性的偏好关系确定的效用函数是严格拟凹函数。

回到原题。欲证明Hessi矩阵在给定的子空间上半负定。现任取

和线性子空间

上的变化量

。根据多元函数泰勒公式，

，满足

.移项得：

.易知全微分

在线性子空间

上为零；根据偏好的严格凸性， 一定有

.（否则成锐角，不在该子空间中）。所以，等号右侧小于等于零，即

.

这个二阶微分如何理解？我们先看二元的情况。

一般地，

，其中

是Hessi矩阵。这是一个二次型。

回到原题中，于是得到，

，

，所以Hessi矩阵在子空间上半负定。□

其实，我们不需要用这个复杂并且超纲的二阶条件，也可以给出一个很简单的证明：

反证。假如满足一阶条件的点不一定是最优解，那么假设

满足一阶条件，另一个

满足

，且

.一阶条件告诉我们

，

严格凸的偏好关系告诉我们

，

由于

（上文已说明），所以

，可是根据一阶条件，

，根据预算限制，

，所以

，矛盾！□

至此，我们终于证明了：只使用一阶条件就可以得出最优解的充分条件是：解不是角点解，并且偏好满足严格凸性。

周黎安教授第三讲最后一张ppt

---

四、消费者最优解的性质

根据一阶条件，

，我们可以得到以下几条性质。

性质1 边际效用之比等于价格之比

对于任意的i，j，都有：

，即

边际效用之比等于价格之比。

性质2 等边际法则

，即在最优解时，多花一块钱，无论花在哪里，边际效用应相等。

如何理解等边际法则？我们举个例子。假如你要参加高考，现在同样是学习1个月，学数学能提高10分，学语文能提高20分，你学哪个？当然学语文。语文学的好了，再提分就难了，所以1个月能提高的分数就会减少。当各科的“时间的边际分数”都相等时，分数就达到了最高。

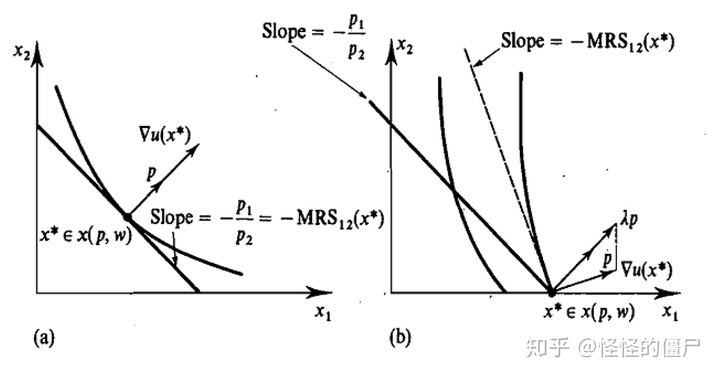
性质3 无差异曲线与预算线相切

根据前面关于边际替代率的讨论，再利用等边际法则：

.即价格之比等于边际替代率之比。

这很好理解，边际替代率之比是个人认为两种商品相互替代的比率，而价格之比是市场上的交换比率。因此达到均衡时，必然价格之比等于边际替代率之比。

那么，如何理解最优解的边际效用之比等于价格之比呢？我们设想如果边际替代率与价格比率不同会发生什么。假定有两种商品，在某点MRS为

而价格之比

，这意味着消费者愿意放弃两单位的商品1，以获得一单位的商品2.但市场愿意以1：1交换它们。那显然消费者会主动减少商品1的购买而选择商品2，这种交换会提高消费者的效用。所以此时并非最优解。

性质4

的含义

是收入的边际效用。具体推导和解释需要引入间接效用函数，请看下一讲。

---

五、举个例子

我们以Cobb-Douglas偏好为例，推导其需求函数，体会现代经济学中“需求”的来历。假设有两种商品，效用函数为

，其中

.为简化计算，作单调变换，效用函数为

。

拉格朗日函数

对各个分量求偏导，

联立解得

，

.

则产生了一个映射

，这个向量函数称为需求函数。

固定

不变，对于某种商品，固定其它商品价格不变，则产生一个一元函数

.它的图像就是我们所说的“需求曲线”。

容易看出，柯布道格拉斯偏好的需求曲线是双曲线。还可以看出，柯布道格拉斯偏好的需求有一个特殊的性质：每种商品的需求量只与这种商品的价格和预算有关，与其它商品的价格无关。这是一种很特殊的性质。一般而言，某种商品价格变化也会引起其它商品的需求量的变化，这就是所谓“替代”与“互补”。可以看出满足柯布道格拉斯偏好的商品既不替代、也不互补。为具体研究一般情况下的替代与互补，我们需要详细研究价格变化对需求的影响。请关注下篇文章的讨论。

---

至此，我们计算出了需求，并初步得出了需求的一些简单性质。但想要回答文章开头提出的“需求曲线向下倾斜”这个结论是否成立的问题，我们做的还远远不够。请关注下一讲。