2020-2-21 深度学习笔记10 - 序列建模：循环和递归网络 1（展开计算图，循环神经网络--经典 / 导师驱动 / 唯一单向量输出 / 基于上下文RNN建模）

第十章 序列建模：循环和递归网络

官网

循环神经网络（recurrent neural network）或RNN是一类用于处理序列数据的神经网络。

循环神经网络（Recurrent Neural Network, RNN）是一类以序列（sequence）数据为输入，在序列的演进方向进行递归（recursion）且所有节点（循环单元）按链式连接的递归神经网络（recursive neural network） 。
循环神经网络具有记忆性、参数共享并且图灵完备（Turing completeness），因此在对序列的非线性特征进行学习时具有一定优势 。循环神经网络在自然语言处理（Natural Language Processing, NLP），例如语音识别、语言建模、机器翻译等领域有应用，也被用于各类时间序列预报。引入了卷积神经网络（Convoutional Neural Network,CNN）构筑的循环神经网络可以处理包含序列输入的计算机视觉问题。

卷积网络在二维图像拓扑上是最成功的

• 专门用于处理网格化数据X（如一个图像）的神经网络
• 可以很容易地扩展到具有很大宽度和高度的图像，以及处理大小可变的图像

循环神经网络主要用于处理一维序列数据。

• 循环神经网络是专门用于处理序列x⁽¹⁾,…,x^(τ)的神经网络
• 可以扩展到更长的序列（比不基于序列的特化网络长得多）
• 大多数循环网络也能处理可变长度的序列

循环神经网络和神经网络区别

两者最大的不同就是循环神经网络可以根据过去做到未来。
我们可以根据不同的训练准则，选择性的精确保留过去序列的某些方面。
下图为神经网络与循环神经网络的对比。
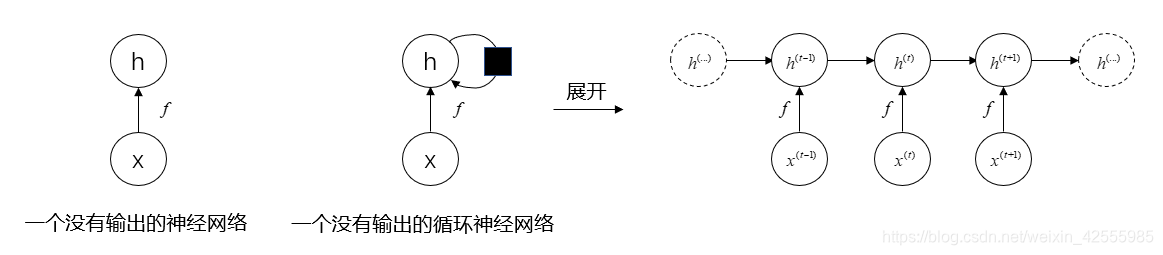在图中可以看到一个普通的神经网络就是将输入x通过函数f的计算再到状态h。而循环神经网络顾名思义就是一个循环过程，这个循环网络只处理来自输入X的信息，将其合并到经过时间向前传播的状态h，f是数据的处理函数。可以发现当前状态是可以影响其未来的状态。

展开计算图

计算图是形式化一组计算结构的方式，如那些涉及将输入和参数映射到输出和损失计算。

以下在反向传播中曾经介绍过
【1.计算图定义】
我们使用图中的每一个节点来表示一个变量。变量可以是标量、向量、矩阵、张量、或者甚至是另一类型的变量。
为了形式化我们的图形，我们还需引入操作(operation)这一概念。操作是指一个或多个变量的简单函数。
我们的图形语言伴随着一组被允许的操作。我们可以通过将多个操作复合在一起来描述更为复杂的函数。
如果变量 y 是变量 x 通过一个操作计算得到的，那么我们画一条从 x 到 y 的有向边。我们有时用操作的名称来注释输出的节点，当上下文很明确时，有时也会省略这个标注。

【2.不同操作对应的计算图举例】

• 使用 × 操作计算 z = xy 的图

• 用于逻辑回归预测 yˆ = σ(x^⊤w + b) 的图。一些中间表达式在代数表达式中没有名称，但在图形中却需要。我们简单地将 第 i 个这样的变量命名为 u⁽ⁱ⁾

• 表达式H = max{0, XW + b} 的计算图，在给定包含小批量输入数据的设计矩阵 X 时，它计算整流线性单元Relu( g(z)=max{0,z} )激活的设计矩阵 H。

• 对变量实施多个操作也是可能的。该计算图对线性回归模型的权重 w 实施多个操作。这个权重不仅用于预测 yˆ，也用于权重衰减罚项$\lambda {\sum }_i{w}_i^2$。这就是所谓的结构化风险评估。

【3.展开RNN计算图】

我们对展开(unfolding) 递归或循环计算得到的重复结构进行解释，这些重复结构通常对应于一个事件链。展开（unfolding) 这个图导致深度网络结构中的参数共享。

$a.动态系统的经典形式计算图$
例如，考虑动态系统的经典形式：
$$s^{(t)}=f(s^{(t-1)};\theta )$$
其中$s^{(t)}$称为系统的状态。
$s$在时刻$t$的定义需要参考时刻$t-1$时同样的定义，因此上式是循环的。
对有限时间步$\tau$， $\tau -1$次应用这个定义可以展开这个图。
例如$\tau =3$，我们对上式展开，可以得到：
$$s^{(3)}=f(s^{(2)};\theta )=f(f(s^{(1)};\theta );\theta )$$
以这种方式重复应用定义，展开等式，就能得到不涉及循环的表达。

现在可以使用传统的有向无环计算图（和隐马尔可夫模型HMM一样都是有向无环图概率图模型）表示这样的表达。

每个节点表示在某个时刻 t 的状态，并且函数 f 将 t 处的状态映射到 t + 1 处的状态。所有时间步都使用相同的参数(用于参数化 f 的相同 θ 值)

$b.存在外部驱动信号的动态系统的计算图$
另一个例子，让我们考虑由外部信号$x^{(t)}$驱动的动态系统，
$$s^{(t)}=f(s^{(t-1)},x^{(t)};\theta )$$
为了表明状态是网络的隐藏单元，我们使用变量 h h