深入理解与应用Logistic回归模型

本文还有配套的精品资源，点击获取

简介：Logistic回归模型是统计学中用于二分类问题的重要工具，通过线性回归与对数几率函数的结合，将预测结果转换为概率值。本文介绍了该模型的基础、形式、参数估计、评估、应用、扩展、优缺点、局限性以及模型的选择与优化方法。特别强调了Logistic回归在多个领域中的应用案例，以及在实际数据分析中软件工具的使用。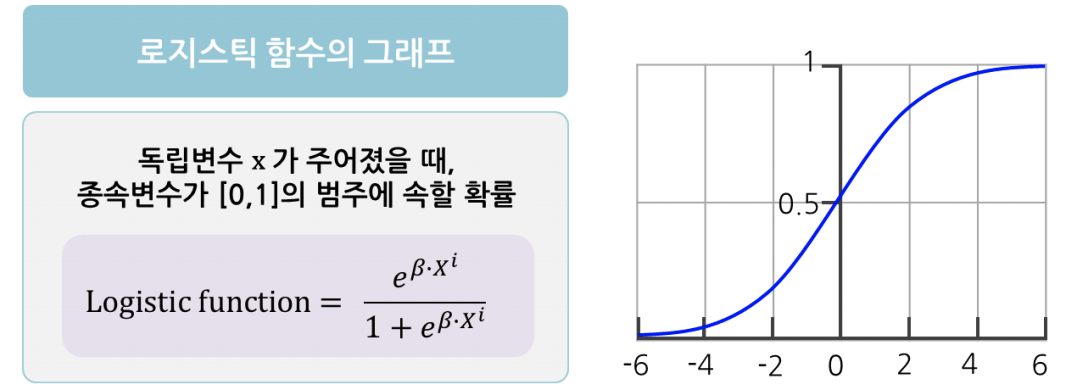

1. Logistic回归模型基础

在数据分析和机器学习领域，Logistic回归模型是一种广泛应用于分类问题的统计方法。它特别适用于处理因变量为二分类的情况，如是/否、成功/失败。模型的核心思想是将线性回归模型的输出，通过Logistic函数，即Sigmoid函数转化为一个概率值，以此来进行分类决策。虽然名为“回归”，但Logistic回归实际上是一种分类算法，其模型形式简单、易于理解和实现，在医疗、金融和其他多个领域有着重要的应用价值。在接下来的章节中，我们将深入探讨Logistic回归的数学原理、参数估计、模型评估、应用场景以及如何在实际中进行软件实现。

2. Logistic回归模型的形式与理论

2.1 Logistic回归模型的数学表达

2.1.1 概率与几率的概念

Logistic回归模型是一种广泛应用于分类问题的统计方法，其基础是概率论。概率是衡量某个事件发生的可能性的度量，取值范围在0到1之间。在二元分类问题中，一个事件发生的概率记为P，不发生的概率则为1-P。几率（Odds）是事件发生的概率与不发生的概率的比值，数学表达为P/(1-P)。

例如，如果一个邮件是垃圾邮件的概率是0.6，那么不是垃圾邮件的概率是0.4，因此垃圾邮件与非垃圾邮件的几率是0.6/0.4，即1.5。几率可以大于1（事件发生的可能性大于不发生的可能性），也可以小于1（事件发生的可能性小于不发生的可能性），还可以等于1（事件与不发生的可能性等同）。

2.1.2 逻辑函数的引入及其数学性质

为了能够将线性回归模型推广到分类问题中，引入了逻辑函数（Logistic Function），也称为Sigmoid函数，其数学表达式为：

[ \sigma(z) = \frac{1}{1 + e^{-z}} ]

Sigmoid函数的特点是输入可以取任意实数值，而输出的值在(0,1)之间，正好对应于概率的取值范围。其图形是一个S形曲线，如下所示：

graph LR
A[z] --> B[sigmoid(z)]
B --> C[0...1]

Sigmoid函数的数学性质使得它非常适合用于将线性回归的输出转换为概率。具体来说，当z趋于正无穷时，Sigmoid(z)趋近于1，表示事件发生的概率接近100%；而当z趋于负无穷时，Sigmoid(z)趋近于0，表示事件发生的概率接近0%。

2.2 Logistic回归模型的形式分类

2.2.1 二分类Logistic回归

二分类Logistic回归是最简单的形式，其目标是预测一个事件发生与不发生的概率。在二分类问题中，Logistic回归模型的输出是样本属于某一类的概率。假设有一个因变量Y，它可以取两个值（通常为0和1），则模型可以表示为：

[ P(Y=1|X) = \sigma(\beta_0 + \beta_1 X_1 + \beta_2 X_2 + ... + \beta_n X_n) ]

其中，( \beta_i ) 是模型参数，( X_i ) 是特征变量，( n ) 是特征的数量。通过这种方式，模型可以输出一个介于0和1之间的概率值，表示给定特征向量X下，事件发生的概率。

2.2.2 多分类Logistic回归

在实际应用中，经常需要处理超过两个类别的分类问题，即多分类问题。多分类Logistic回归通常有以下几种处理方式：

• 一对一策略 （One-vs-One, OvO）：对于k个类别的分类问题，训练k(k-1)/2个分类器，每个分类器区分两个类别。在预测时，对每个分类器的结果进行投票，选择得票最多的类别。
• 一对剩余策略 （One-vs-Rest, OvR）：为每个类别训练一个分类器，这些分类器将该类别与所有其他类别区分开来。在预测时，选择概率最高的分类器对应的类别作为最终的预测结果。

对于多分类问题，可以将Logistic回归的输出设置为k个Sigmoid函数，每个函数对应一个类别，这种模型也称为softmax回归。其形式如下：

[ P(Y=i|X) = \frac{e^{\beta_{i0} + \beta_{i1} X_1 + ... + \beta_{in} X_n}}{\sum_{j=1}^{k} e^{\beta_{j0} + \beta_{j1} X_1 + ... + \beta_{jn} X_n}} ]

2.2.3 序数Logistic回归

序数Logistic回归适用于处理序数数据（有序类别数据）。在序数分类问题中，类别之间存在顺序关系，例如评价等级（差，中，好）。序数Logistic回归不是简单地预测类别的概率，而是预测每个类别相对于参照类别的相对概率。

序数Logistic回归模型通常会使用所谓的“累计”或“比例”概率，例如：

[ P(Y \leq j | X) = \frac{e^{\beta_0 + \beta_1 X_1 + ... + \beta_n X_n}}{1 + e^{\beta_0 + \beta_1 X_1 + ... + \beta_n X_n}} ]

这里，( j ) 表示类别，而 ( Y \leq j ) 表示样本属于类别j或更低的类别。通过这种方式，可以评估一个样本属于某个类别或更低类别（相对于序数）的概率。

3. Logistic回归模型的参数估计与检验

在第二章中，我们了解了Logistic回归模型的不同形式与理论基础。现在，我们转向对模型参数的估计与检验，这是构建有效预测模型的关键步骤。本章节将详细介绍参数估计的方法论，并探讨参数估计的统计检验方法。

3.1 参数估计的方法论

参数估计是机器学习与统计建模中至关重要的环节。在Logistic回归中，参数估计的目的在于确定模型中的系数，从而使得模型能够最好地拟合数据。

3.1.1 最大似然估计原理

最大似然估计（Maximum Likelihood Estimation，MLE）是一种通过观测数据来估计概率模型参数的方法。简而言之，MLE的目标是找到一组参数，这组参数能使观测到的数据出现的概率最大化。

在Logistic回归中，似然函数（Likelihood Function）是关于模型参数的函数，其表达式为数据出现概率的乘积。我们通过优化似然函数来估计参数。数学上，我们通常对似然函数取对数，将乘法运算转换为加法运算，得到对数似然函数（Log-Likelihood Function），然后通过求导寻找极大值点。

3.1.2 梯度下降法与优化算法

梯度下降法是一种迭代算法，用于求解函数的局部最小值。在参数估计的上下文中，我们将其用于最小化成本函数（例如负对数似然函数），从而找到参数的最优估计值。

梯度下降法的基本思想是从一个初始点开始，按照负梯度方向（即函数下降最快的方向）迭代更新参数，直到收敛。梯度下降法的变种如随机梯度下降（SGD）和批量梯度下降（BGD）提供了不同的更新策略和适用场景。

代码示例 ：

import numpy as np

# 假设X为输入特征矩阵，y为二分类标签
# W为模型参数，初始为零向量
W = np.zeros(X.shape[1])

# 学习率
alpha = 0.01

# 对数似然函数
def log_likelihood(X, y, W):
    # 实现细节省略
    pass

# 梯度计算函数
def gradient(X, y, W):
    # 实现细节省略
    pass

# 梯度下降主循环
for _ in range(iterations):
    W -= alpha * gradient(X, y, W)

在上面的代码块中，我们首先导入numpy库，并初始化参数W。然后，定义了一个计算对数似然的函数和一个计算梯度的函数。最后，通过迭代更新W来执行梯度下降。

3.2 参数估计的统计检验

参数估计之后，我们需要对模型参数进行统计检验以确保它们的统计显著性。统计检验可以帮助我们判断模型系数是否有效地预测了因变量。

3.2.1 偏回归系数的检验

偏回归系数（或称偏回归斜率）衡量的是自变量与因变量之间的关系强度和方向，当我们控制其他变量不变时。检验偏回归系数的显著性，通常使用t检验（t-test）。

在Logistic回归中，每个偏回归系数的t检验涉及以下步骤：

1. 计算偏回归系数的估计值。
2. 计算标准误差（Standard Error，SE）。
3. 计算t统计量，即偏回归系数除以SE。
4. 根据自由度（通常等于样本数量减去参数数量）和希望得到的显著性水平，查找t分布表得到临界值。
5. 将计算得到的t统计量与临界值比较，判断系数是否显著。

3.2.2 模型的似然比检验和Wald检验

似然比检验（Likelihood Ratio Test，LRT）和Wald检验是两种常用的检验方法，用于评估整体模型或模型中特定参数的统计显著性。

似然比检验 的核心思想是：通过比较两个模型的似然函数值来进行假设检验。一个模型包含某个参数，另一个模型不包含。如果包含该参数的模型显著改善了似然值，我们便有理由认为这个参数在统计上是有意义的。

Wald检验 则是基于模型参数估计值和它们的标准误差。检验的统计量是参数估计值除以其标准误差，其分布接近卡方分布。通过将统计量与临界值比较，我们可确定参数是否显著。

Mermaid流程图示例 ：

graph LR
    A[开始] --> B[拟合完整模型]
    B --> C[拟合简化模型]
    C --> D[计算两个模型的似然比]
    D --> E[计算统计量]
    E --> F{统计量是否显著?}
    F -- 否 --> G[接受简化模型]
    F -- 是 --> H[保留完整模型]
    H --> I[结束]
    G --> I

流程图说明了似然比检验的基本步骤，从拟合完整的模型开始，到最终根据检验结果决定模型选择。

通过本章节的介绍，我们已经了解了Logistic回归模型参数估计的主要方法和参数检验的基本概念。在下一章中，我们将深入探讨如何评估和优化Logistic回归模型，以提高其预测性能。

4. Logistic回归模型的评估与优化

4.1 模型评估的基本方法

4.1.1 混淆矩阵与分类精度

混淆矩阵（Confusion Matrix）是评估分类模型性能的一个重要工具。它呈现了模型对于各个类别的预测情况，其中横轴代表预测值，纵轴代表实际值。对于Logistic回归模型，我们可以用以下四种情况来评估模型性能：

• 真正类（True Positive, TP） : 模型正确预测为正类的数量。
• 假正类（False Positive, FP） : 模型错误预测为正类的数量。
• 真负类（True Negative, TN） : 模型正确预测为负类的数量。
• 假负类（False Negative, FN） : 模型错误预测为负类的数量。

根据这些值，可以计算出分类模型的精确度（Precision）、召回率（Recall）和F1分数：

# 伪代码展示混淆矩阵的计算过程
from sklearn.metrics import confusion_matrix

# 假设 y_true 是真实标签，y_pred 是模型预测标签
tn, fp, fn, tp = confusion_matrix(y_true, y_pred).ravel()

# 计算精确度、召回率和F1分数
precision = tp / (tp + fp)
recall = tp / (tp + fn)
f1_score = 2 * (precision * recall) / (precision + recall)

4.1.2 ROC曲线与AUC值

接收者操作特征曲线（Receiver Operating Characteristic，简称ROC曲线）是另一种评估二分类模型性能的有效方法。ROC曲线通过不同的阈值下计算真正类率（True Positive Rate，TPR）与假正类率（False Positive Rate，FPR）来展示模型的分类能力。

ROC曲线越接近左上角，模型的性能越好。衡量ROC曲线整体性能的一个数值是曲线下面积（Area Under the Curve，简称AUC）。AUC的值介于0到1之间，一个理想的分类器的AUC值为1。

# 伪代码展示ROC曲线和AUC值的计算过程
from sklearn.metrics import roc_curve, auc

# 假设y_scores是预测的分数
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)

# 绘制ROC曲线
import matplotlib.pyplot as plt

plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

4.2 模型选择与优化策略

4.2.1 模型选择的标准

模型选择是机器学习任务中的一个重要环节，它涉及到根据一系列标准从多个候选模型中选择出最佳模型。对于Logistic回归模型而言，常用的模型选择标准包括：

• 交叉验证分数（Cross-validation Score） : 通过交叉验证计算模型在不同数据集上的平均表现。
• AIC（赤池信息量准则） : AIC是一种衡量模型复杂度和拟合优度的准则，较低的AIC值通常表示模型更为可取。
• BIC（贝叶斯信息量准则） : BIC类似于AIC，但惩罚项更大，对于具有更多参数的模型更加严格。

4.2.2 正则化方法与模型压缩

为了防止模型过拟合，尤其是当样本特征数量较多时，可以采用正则化方法对Logistic回归模型进行优化。正则化方法通过对模型参数的大小施加限制，从而减少模型复杂度。常见的正则化方法有：

• L1正则化（Lasso回归） : 通过添加绝对值作为惩罚项，鼓励模型选择稀疏特征。
• L2正则化（Ridge回归） : 通过添加平方项作为惩罚项，对参数值较大进行惩罚。

正则化项可以表示为：

# 伪代码展示正则化项的计算
import numpy as np

# 假设theta是模型参数，alpha是正则化强度参数
l1_penalty = alpha * np.sum(np.abs(theta))
l2_penalty = alpha * np.sum(np.square(theta))

在实践中，正则化参数 alpha 可以通过交叉验证进行选择。

模型压缩则是将一个大模型转换成小模型的过程，目的是减少模型的复杂度并提高运算效率。在Logistic回归中，使用L1正则化即可达到模型压缩的目的，因为L1正则化倾向于产生稀疏解，有助于去除一些不重要的特征。在实际应用中，一旦模型经过了正则化训练，就可能得到一个较为精简的模型版本。

5. Logistic回归模型的应用场景

5.1 Logistic回归在医疗领域的应用

5.1.1 疾病风险预测

在医疗领域，Logistic回归模型被广泛用于疾病风险预测。这是因为Logistic回归能够处理分类输出，非常适合于预测疾病的发生与否。例如，我们可以利用Logistic回归模型，基于病人的年龄、性别、生活习惯、遗传因素等数据，来预测某病人患有某种疾病的可能性。

该模型可以预测的疾病包括但不限于心脏病、糖尿病、癌症等。模型的预测结果为概率值，可以根据医疗需求设定阈值，超过阈值即可认为该病人存在患病的风险。在实际的医疗应用中，Logistic回归模型需要和医生的专业知识结合使用，才能达到更好的效果。

5.1.2 临床决策支持系统

Logistic回归模型在临床决策支持系统（CDSS）中也扮演着重要的角色。临床决策支持系统依赖于大量的数据和先进的数据分析方法来辅助医生进行决策。

在CDSS中，Logistic回归可以被用于根据病人的临床数据来预测治疗的效果和可能的副作用。通过对大量的病例数据进行分析，Logistic回归模型能够辨识出对治疗效果和副作用有显著影响的因素，并据此对新病例进行预测。

这类系统可以显著提高医疗决策的质量，减少医疗错误，并帮助医生更好地了解病情、制定治疗方案。然而，需要注意的是，Logistic回归模型给出的是基于统计数据的预测，医生在临床实践中仍需要综合考虑患者的实际情况。

5.2 Logistic回归在金融领域的应用

5.2.1 信用评分模型

在金融领域，信用评分模型是核心应用之一。金融机构利用Logistic回归模型来评估个人或企业的信用风险，进而决定是否给予贷款、信用卡额度等服务。

具体来说，信用评分模型会考虑个体的收入水平、负债情况、信用历史和其他相关因素来预测违约的概率。金融机构可以使用这些预测结果来做出贷款决策，并决定贷款利率。

这种模型的一个重要优势是其直观性和解释性，相较于机器学习中的其他复杂模型，Logistic回归的结果更加容易被解释和理解。尽管如此，在实际应用中，信用评分模型需要定期进行验证和调整，以保证其准确性。

5.2.2 市场营销响应预测

Logistic回归模型也常用于市场营销领域，尤其是在响应预测中。通过分析客户的历史行为数据、人口统计学特征以及购买行为，Logistic回归模型可以帮助企业预测客户对于市场营销活动的响应概率。

比如，通过分析客户对过往邮件营销活动的点击率和购买记录，企业可以构建一个Logistic回归模型，来预测哪些客户更可能响应即将推出的新活动。这可以帮助企业更加精准地进行市场定位，提高营销活动的ROI（投资回报率）。

在实际应用中，企业需要收集大量相关的客户数据，并且不断地更新和维护模型，以保证预测结果的准确性。同时，企业还需要关注隐私保护和数据安全，确保在合理合法的范围内使用客户数据。

5.2.3 代码实践

# 使用Python中的scikit-learn库来实现一个简单的信用评分模型

import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import classification_report, roc_auc_score

# 假设我们有一个名为credit_data的数据集
credit_data = pd.read_csv('credit_data.csv')

# 选择特征和目标变量
features = credit_data[['age', 'debt', 'income', 'assets', 'credit_history']]
target = credit_data['default']

# 将数据集分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(features, target, test_size=0.2, random_state=42)

# 创建Logistic回归模型实例
model = LogisticRegression()

# 训练模型
model.fit(X_train, y_train)

# 预测测试集
y_pred = model.predict(X_test)

# 输出模型评估报告
print(classification_report(y_test, y_pred))

# 输出ROC AUC得分
print('ROC AUC Score:', roc_auc_score(y_test, model.predict_proba(X_test)[:, 1]))

在这段代码中，我们首先导入了必要的库，并加载了credit_data数据集。然后，我们选取了特征变量和目标变量，并将数据集分割为训练集和测试集。接着，我们创建了一个Logistic回归模型实例，并用训练集对模型进行了训练。最后，我们使用测试集对模型进行了评估，并输出了分类报告和ROC AUC得分。

需要注意的是，为了得到良好的预测性能，数据预处理和特征工程也是至关重要的。在实际应用中，特征的选择、编码以及处理缺失值和异常值都是需要特别注意的步骤。

在模型部署之后，监控模型性能和及时更新模型以反映最新的数据趋势也是必要的。这样，我们能够确保模型在实际的金融业务中发挥最大的作用。

6. Logistic回归模型的软件实现与实践

在了解了Logistic回归的理论和参数估计之后，接下来探讨的是Logistic回归的软件实现与实践。我们将通过R语言和Python这两种常用的数据分析和机器学习工具，来详细解析Logistic回归的软件实现，并通过实际案例来演示如何在真实数据集上执行Logistic回归模型。

6.1 常用统计软件实现Logistic回归

6.1.1 R语言中的Logistic回归分析

R语言是统计分析领域中非常流行的开源软件之一。在R中，我们可以使用 glm() 函数来拟合Logistic回归模型。它不仅支持线性模型，还能处理广义线性模型，是处理二元、多项式和序数Logistic回归的理想选择。

# 加载数据集
data("mtcars")
# 假设我们使用mpg(每加仑英里数)来预测是否为自动变速器(am=1为自动，am=0为手动)
mtcars$am <- as.factor(mtcars$am)
logit_model <- glm(am ~ mpg, data=mtcars, family=binomial)
summary(logit_model)

在上述代码中， mtcars 是R内置的汽车数据集，我们将 am 列转换为因子类型，以适应二元Logistic回归。 glm 函数的 family 参数设置为 binomial 来指定模型类型。 summary() 函数用于查看模型的详细统计信息。

6.1.2 Python中的Logistic回归应用

Python是机器学习和数据科学领域中非常受欢迎的编程语言。在Python中，我们可以使用 scikit-learn 库来实现Logistic回归。

# 导入所需的库
from sklearn.linear_model import LogisticRegression
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
import pandas as pd

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 进行数据集划分
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 创建模型并训练
logit = LogisticRegression(max_iter=200)
logit.fit(X_train, y_train)

# 模型预测与评估
predictions = logit.predict(X_test)

上述代码使用了鸢尾花数据集，将数据集分为训练集和测试集，随后创建并拟合了一个 LogisticRegression 模型。最后，我们使用训练好的模型对测试集进行预测。

6.2 实际案例分析与代码实践

6.2.1 数据预处理与探索性数据分析

在应用Logistic回归模型之前，我们首先需要对数据进行预处理和探索性数据分析，以确保数据质量并找到合适的变量进行建模。

import seaborn as sns
import matplotlib.pyplot as plt

# 绘制特征和目标变量之间的关系
sns.countplot(x="am", data=mtcars)
plt.show()

# 两变量间的关系图
sns.scatterplot(x="mpg", y="wt", data=mtcars, hue="am")
plt.show()

上述代码展示了如何使用Python的 seaborn 库来绘制分类变量 am 的分布情况以及连续变量 mpg 和 wt 与 am 之间的关系。

6.2.2 代码实现与结果解读

在R或Python中实现Logistic回归后，我们可以查看模型的输出结果并解读它们。

# 输出R中Logistic回归模型摘要
summary(logit_model)

# Python中模型的系数
print("Coefficients:", logit.coef_)

在R的 summary 结果中，我们可以看到每个变量的回归系数估计值、标准误、z值、p值等统计信息。在Python中，模型的系数直接输出，我们可以解释为每个特征的对数几率比。

6.2.3 模型的部署与监控

部署Logistic回归模型通常意味着将模型集成到生产环境中，并确保其稳定运行。监控是确保模型长期表现的关键。

# 保存模型
import joblib
joblib.dump(logit, 'logistic_regression_model.pkl')

# 加载并使用模型
loaded_model = joblib.load('logistic_regression_model.pkl')
loaded_model.predict(X_test)

在Python中，我们可以使用 joblib 库来保存和加载模型。这样，在新的数据上我们可以快速使用训练好的模型进行预测。

监控模型的性能可以通过定期检查模型的准确度、AUC值等关键性能指标来实现。如果性能下降，可能需要重新训练模型或调整模型参数。

总结来说，Logistic回归的软件实现涉及数据预处理、模型训练、结果解读以及模型部署与监控等多个步骤。通过上述的R语言和Python实践案例，我们可以看到如何在实际应用中将这些步骤一一实现。这不仅要求我们掌握模型本身的知识，还包括了编程技能和数据处理技巧。

本文还有配套的精品资源，点击获取

简介：Logistic回归模型是统计学中用于二分类问题的重要工具，通过线性回归与对数几率函数的结合，将预测结果转换为概率值。本文介绍了该模型的基础、形式、参数估计、评估、应用、扩展、优缺点、局限性以及模型的选择与优化方法。特别强调了Logistic回归在多个领域中的应用案例，以及在实际数据分析中软件工具的使用。

本文还有配套的精品资源，点击获取