量化感知训练——LSQ(一：原理)

1. 什么是模型量化

 个人总结：对浮点型(float)的模型参数(weight)和激活值(activation)通过某个映射，离散化成整型，如将float的参数通过一个线性映射变成int8的整型。

        比如这个线性映射可以如下：

                                                                                   (1)
             其中  为float类型的参数， 为缩放参数scale,  为偏置，也称为零点值(zeropoint), 就是当  为0是，对应的量化值；  为量化后的值。 

                                  
2. 为什么要模型量化

       模型量化的目的是为了将float类型的计算，变成整型的计算。比如我们一般PC端训练的模型的参数是float32类型，在计算时占的位宽32; 而比如int8的位宽只有8(int4的位宽只有4，等等)， 使用量化后的int8来进行模型的推理计算，然后再反量化得到最终输出，显然提升了计算速度，减少了计算内存的空间。但是，将float32量化成int8进行推理后再反量化回来，结果显然是容易产生误差的；比如：有一个tensor: 

                    

现在我们需要将这个tensor量化到uint8, 也就是[0, 255]。

根据公式(1)，首先计算 , ：

                                                                                     (2)

                                                                                 (3)

           把数值带入(2), (3)得：

那么此时进行反量化还原的话：

量化前的tensor：  ，

量化后的qtensor: 

显然两者是有误差的。这种误差的积累将导致模型推理的结果发生改变，发生改变往往意味着模型量化后的准确率会变低。因此，模型量化需要解决的一个最重要的问题就是量化后如何保证推理的准确率。

3. 怎么进行量化

一般一下种方式：

后训练量化(Post-trainging quantization, 简称PTQ)：

       对训练后的模型参数，利用统计学或者其他一些方法，找到一个合理的映射，把float型离散化为整型。

量化感知训练(Quantization Awaring training, 简称QAT)

        通过在训练中模拟量化的过程（如何模拟这个量化的过程，这就是各种量化训练方法要解决的问题），然后再对模拟量化的节点进行反量化，通过更新参数使得参数适应量化过程保持准确率尽量不下降。
5. 量化感知训练

前面说了量化感知训练是什么，那么其中两核心个问题：

1. 怎么模拟量化过程？

插入伪量化节点：对训练的weight和激活值进行量化，然后再反量化得到新的weight和激活值，利用新的weight和激活值进行前向计算。

2. 怎么更新参数？

直通估计(Straight Through Estimator 简称STE):在反向传播中，由于反量化后得到的新的的偏导处处为零(round取整操作的导数为0)， 跳过伪量化的过程，直接对伪量化之前的进行更新，通过伪量化得到的计算的结果来模拟量化误差，通过这个误差来反向修正原始的,以适应量化产生的误差。

4. QAT算法——LSQ算法原理介绍

LSQ算法是一种经典的QAT算法，LSQ全称为learning Step Size Quantization;

主要的算法思想：通过插入伪量化节点，通过量化训练来学习量化参数scale并不断更新scale, 以达到量化的目的。与其他的量化训练不同的是，网络学习不仅是调整weight来适应量化误差，还加入了scale（lsq+加入了偏移offset的学习），通过对scale的学习来适应量化误差。

核心问题：如何更新量化参数scale?

首先LSQ也是插入伪量化节点，也是利用STE来更新参数。

伪量化的前向计算如下：

那么weight的伪量化的过程可由下列公式表示(这里假如LSQ的量化为对称量化)：

                                                        (4)

                                                                                                  (5)

其中，clip代表截断操作，round代表取整操作。 是 float 的输入，是量化后的数据 (仍然使用 float 来存储，但数值由于做了 round 操作，因此是整数)，是反量化的结果。 和  分别是量化数值的最小值和最大值 )， 是量化参数。

通过公式(4), (5)合并为下公式：

 对求导得：

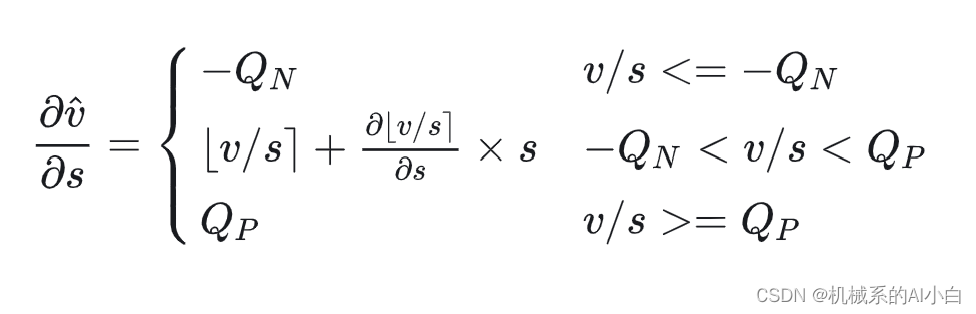
其中：

得到（ ∂⌊𝑡⌉/∂𝑡 是 STE 得到）：

通过以上公式的推到，我们得到了插入伪量化节点后，被量化参数对scale参数的偏导，也就知道了通过训练学习scale的理论基础。

        在计算 𝑠 的梯度的时候，需要注意其参数更新的幅度和权重参数更新的幅度是成比例的，这有助于训练更好的收敛, ratio定义如下：

                                         

        算法参数初始化和s的梯度调整：

每一层的权重(weight)或激活值(activation)有对应的s(scale), 一般可以初始化为  ： 量化训练的权重（weight）的初始化可由预训练好的float模型的权重得到，激活值的初始化可由一些代表性的数据进行推理计算得到。

为了在训练中更好的收敛，对s的梯度进行调整，用s乘以一个gradient scale，记作g。对于权重,

, 其中为每一层中权重的个数，对于激活值，，其中为每层激活值中特征的个数。