常用涡识别方法的Tecplot实现（Q准则、λ2 准则、delta准则、Omega准则）

惯例声明：本人没有相关的工程应用经验，只是纯粹对相关算法感兴趣才写此博客。所以如果有错误，欢迎在评论区指正，不胜感激。本文主要关注于算法的实现，对于实际应用等问题本人没有任何经验，所以也不再涉及。

本来想写一个拉格朗日结构LSC的文章，但是不知道是算法理解有问题还是计算参数设置问题，自己搞的结果总是神似形不似，所以放弃，改写一个偏实际应用方面的。

0 前言

0.1 欧拉法涡识别

欧拉法涡识别基于函数与场论的思想，对流场的信息进行计算加工，得到描述涡的函数。之后对涡函数取截面或等值面等方法，展示涡的结构。

大多数欧拉法涡识别都具有平移不变性，即涡识别结果不会因为场的平移而变化。
但是大多数欧拉法涡识别都不具备旋转不变性，即涡识别结果会因为坐标系定义的方向变化而变化（尤其是旋转坐标系下的涡识别）。

常用的涡识别方法有涡量法、Q方法、λ2方法（Lambda-2）、Δ方法（Delta）、λci方法（Lambda-ci)、Ω方法(Omega）。具体的原理不再细说，本文只介绍最终结果。

本文的参考文献以及术语定义来源为：
[1]第三代涡识别方法及其应用综述（王义乾, 桂南）2019
[2]A review of methods for vortex identification in hydroturbines（张宇宁）2018
[3]Tecplot官方Github：https://github.com/Tecplot/handyscripts/tree/master/macro

0.2 Tecplot中的涡识别

Tecplot在新版本中陆续添加了很多新的涡识别方法，以Q准则为例。

第一步，点击Analyze中的Calculate Variables

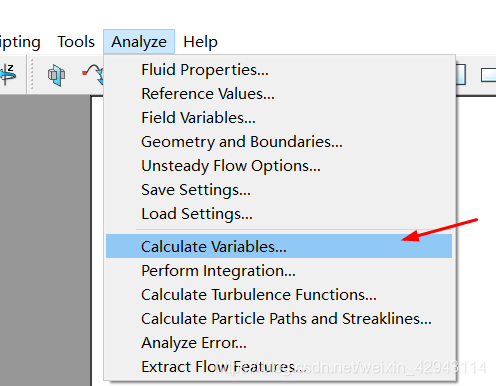
第二步，点击Select，选择Q Criterion，选择Ok。然后点击Calculate计算即可。

如果由于Tecplot的版本太低，或者想要计算的涡识别方法没有被Tecplot收录，就需要自己计算编辑计算了。当然，优先用Tecplot自带的函数计算，那些函数计算经过优化更省时间。
那么可以采取下面的方法：
第一步，点击Data里的Alter，选择Specify Equations

第二步：输入公式，点击Compute计算（这里用到的公式在后面会给出，不用抄）

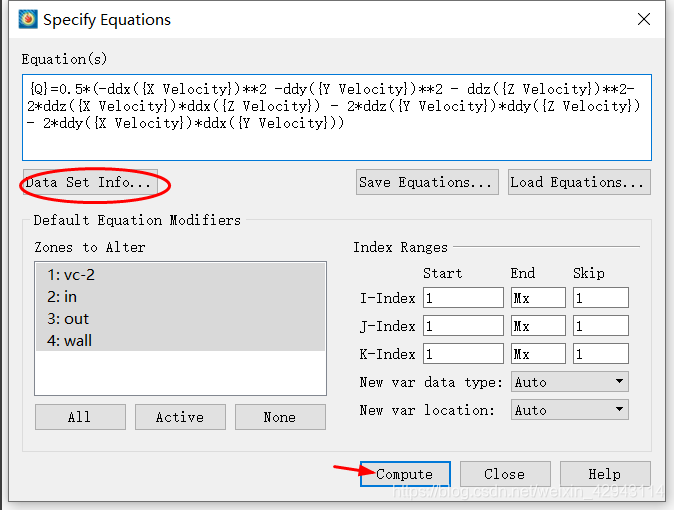
这里注意Tecplot的公式格式：
1 次方用的不是^，而是**
2 变量用花括号{}括起来，具体变量名称参考Data Set Info里面，不同软件不同设置得到的变量名称往往不一样。（也可以用V3来的形式，来表示第3个变量，变量顺序同样参考Data Set Info）

1 涡量法

涡量法是描述涡最简单的方法，但是难以区分旋转导致的涡与剪切导致的涡（比如会把边界层识别出来）。而且难以识别虽然涡量较小但是结构清晰的涡。

Tecplot内Analyze中的Calculate Variables中，自带函数Vorticity Magnitude计算涡量。
由于内置函数计算速度远大于自己编辑的公式，所以不再给出函数。

2 Q方法

这个是最经典的方法，计算量小，而且结果也很不错，推荐使用。

一般选择Q>0的某个等值面作为涡。

Tecplot内Analyze中的Calculate Variables中，自带函数Q Criterion
由于内置函数计算速度远大于自己编辑的公式，所以尽可能用Tecplot内的函数。

公式为
$$Q=0.5\ast (\Vert B{\Vert }_F^2-\Vert A{\Vert }_F^2)$$
其中，$\Vert B{\Vert }_F^2$表示矩阵B的范数的平方，等同于矩阵B所有元素的平方和。
而矩阵A和矩阵B分别为速度梯度的对称张量和反对称张量，即：
$$A=0.5\ast (\Delta V+\Delta V^T)$$
$$B=0.5\ast (\Delta V-\Delta V^T)$$
其中T代表矩阵的转置。速度张量的定义如下：
$$\Delta V=(\begin{array}{c}\text{Ux}\end{array}$$