算法介绍
0-1背包问题是一个经典的组合优化问题,通常用于描述以下情境:①有一个容量有限的背包,可以容纳一定总重量的物品。②有一组不同的物品,每个物品都有一个特定的重量和一个价值。③目标是在限定的背包容量内,选择一些物品放入背包,以使这些物品的总重量不超过背包容量,同时使它们的总价值最大化。
0-1背包问题的名称来自于每个物品在解中要么被完全放入背包(0表示不放入,1表示放入),而不允许将物品部分放入背包。它是一个NP难问题,没有一个多项式时间的精确解法,因此通常使用动态规划、贪心算法或启发式算法等近似方法来解决。其中,动态规划是解决0-1背包问题最常见且最有效的方法。
问题描述
给定一组不同的物品,每个物品具有两个属性:重量(weight)和价值(value)。同时,有一个容量有限的背包,容量为W。问题的目标是确定如何选择这些物品放入背包,以使它们的总重量不超过W,并且总价值最大。
问题特点
- 每个物品要么被放入背包(选中),要么不放入背包(不选中),不能部分选择。
- 每个物品只能使用一次。
- 物品的数量和容量都是有限的。
- 目标是最大化背包中物品的总价值。
数学描述
- 物品集合:{物品1, 物品2, …, 物品N},其中N是物品的数量。
- 物品重量:{weight[1], weight[2], …, weight[N]},表示每个物品的重量。
- 物品价值:{value[1], value[2], …, value[N]},表示每个物品的价值。
- 背包容量:W。
问题目标
找到一个物品的选择方式,即一个0-1向量 {x1, x2, …, xN},其中xi为0或1,表示物品i是否被选中,以使得以下条件成立:
- Σ(xi * weight[i]) ≤ W,总选择的物品重量不超过背包容量。
- 最大化 Σ(xi * value[i]),总选择的物品价值最大化。
算法步骤
-
问题结构分析
- 明确原始问题:给定一组物品,每个物品都有一个重量 weight[i] 和一个价值 value[i],以及一个容量有限的背包,容量为 W。
- 给出问题表示:我们定义的子问题是这样的,考虑前 i 个物品,背包容量为 w 时的最大总价值,表示为 dp[i][w]。
-
递推关系建立
-
分析最优(子)结构:以选和不选着手找到重叠子问题。
假设我们已经解决了一个子问题 dp[i][w],它表示在考虑前 i 个物品和背包容量为 w 时的最大总价值。现在,我们考虑如何构建原问题 dp[N][W] 的最优解。
- 如果我们不选择放入第 i 个物品,那么最优解就是 dp[i-1][w],即考虑前 i-1 个物品时背包容量为 w 时的最大总价值。
- 如果我们选择放入第 i 个物品,那么最优解就是 dp[i-1][w - weight[i]] + value[i],即考虑前 i-1 个物品时背包容量为 w - weight[i] 时的最大总价值,再加上第 i 个物品的价值 value[i]。
最优子结构的关键在于,无论我们选择放入还是不放入第 i 个物品,原问题 dp[N][W] 的最优解都可以通过子问题的最优解构建而来。这是动态规划的核心特性之一,允许我们使用递推关系将原问题分解成子问题,逐步求解最优解。
-
构造递推公式
- 递推关系(基于最优子结构而来)
- 对于 i > 0 和 w > 0,dp[i][w] 可以按照以下递推关系更新:
dp[i][w] = max(dp[i-1][w], dp[i-1][w - weight[i]] + value[i])
- 对于 i > 0 和 w > 0,dp[i][w] 可以按照以下递推关系更新:
- 递推关系(基于最优子结构而来)
-
-
自底向上计算
-
确定计算顺序(通过递推式确定计算顺序)
-
状态初始化:将初始化的条件搞定
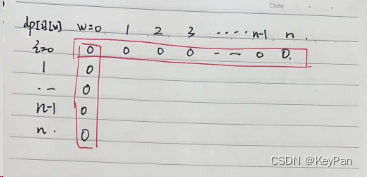
- 对于 i = 0,没有物品可选,所以对于所有 w,dp[i][w] = 0 。
- 对于 w = 0,背包容量为0,所以对于所有 i, dp[i][w] = 0 。
-
明确子问题依赖关系
-
子问题dp[i][w]依赖于子问题 dp[i-1][w-weight[i]]与dp[i-1][w]

dp[i-1][w-weight[i]]与dp[i-1][w]位于dp[i][w]的左上方,故每一行计算都需要把它的上一行算好。
-
-
-
依次求解问题
构造一个备忘录(二维数组 dp )存储子问题的解。从 i=0 到 N(物品的数量),以及从 w=0 到 W(背包容量),按照递推关系依次填充 dp 数组。这是一个自底向上的过程,确保每个子问题都依赖于前面的子问题的解。

-
-
最优方案追踪
最优方案追踪是指在动态规划中找到原问题的最优解,即确定如何选择物品以使总价值最大,同时不超过背包容量。这通常涉及到从填充完动态规划表格后的某个特定单元格开始,然后根据填充过程中的决策来重建最优解。- 从动态规划表格中找到最终状态,即 dp[N][W],其中 N 表示物品的数量,W 表示背包的容量。这个单元格包含了问题的最优解,即最大的总价值。
- 从 dp[N][W] 开始,向前追踪。设当前状态为 dp[i][w],其中 i 表示当前考虑的物品,w 表示当前剩余的背包容量。
- 比较 dp[i][w] 与 dp[i-1][w] 是否相等。如果它们相等,表示当前物品 i 没有被选择放入背包。在这种情况下,继续向上追踪,即令 i 减小 1,不做任何标记。
- 如果 dp[i][w] 与 dp[i-1][w] 不相等,说明当前物品 i 被选择放入背包。在这种情况下,将物品 i 标记为被选中,同时减少背包容量 w,即 w = w - weight[i]。
- 重复上述步骤,直到回到初始状态 dp[0][0],或者 i 等于 1。此时,你已经找到了构成最优解的物品的集合。
- 最后,被标记为被选中的物品组成的集合就是问题的最优解,它们的总重量不超过背包容量 W,总价值最大化。
算法伪代码
这个伪代码描述了0-1背包问题的动态规划算法。算法通过填充一个二维数组 dp 来计算最大总价值,然后使用 traceSolution 函数来回溯找到选中的物品。注意,这个伪代码是一种通用框架,具体的数据结构和输入数据需要根据实际情况进行调整。
函数 knapsack(items, capacity):
n = 数组 items 中物品的数量
创建一个二维数组 dp,大小为 (n+1) x (capacity+1)
对于 i 从 0 到 n:
对于 w 从 0 到 capacity:
如果 i=0 或 w=0:
dp[i][w] = 0 # 基本情况,没有物品或者背包容量为0时,总价值为0
否则如果 items[i-1].weight > w:
dp[i][w] = dp[i-1][w] # 当前物品过重,无法放入背包
否则:
# 考虑将当前物品放入背包和不放入背包两种情况,选择总价值更大的
dp[i][w] = max(dp[i-1][w], items[i-1].value + dp[i-1][w-items[i-1].weight])
返回 dp[n][capacity] 作为最大总价值
函数 traceSolution(items, dp, capacity):
n = 数组 items 中物品的数量
创建一个空数组 selectedItems
w = capacity
对于 i 从 n 到 1(倒序):
如果 dp[i][w] ≠ dp[i-1][w]:
# 当前物品被选中,将其添加到选中的物品列表,并更新背包容量
将 items[i-1] 添加到 selectedItems
w = w - items[i-1].weight
返回 selectedItems 作为选中的物品列表
主程序:
items = 一组物品,每个物品包括 weight(重量)和 value(价值)
capacity = 背包的容量
最大总价值 = knapsack(items, capacity)
选中的物品 = traceSolution(items, dp, capacity)
算法实例
实例介绍
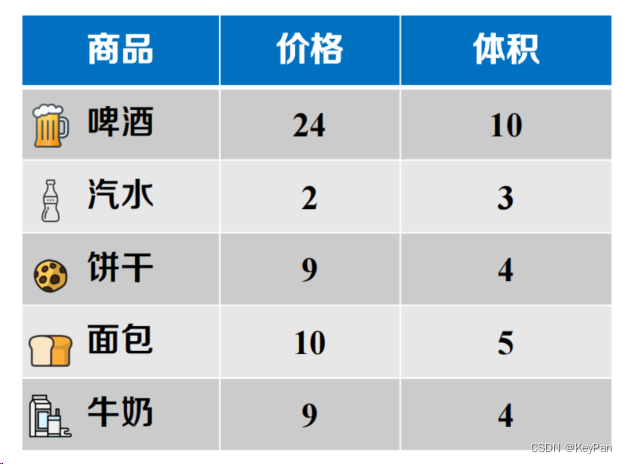
超市允许顾客使用一个体积大小为13的背包,选择一件或多件商品带走。问题:如何带走总价最多的商品?
实例分析
为了方便大家体会动态规划思想的解题步骤中符号的作用,本实例中我换一个符号来表示问题。大家自行体会。
- 问题结构分析
- 明确原始问题
𝑷[𝒊, 𝒄]:前𝒊个商品可选、背包容量为𝒄时的最大总价格。 - 给出问题表示
𝑷[𝒏, 𝑪] :前𝒏个商品可选、背包容量为𝑪时的最大总价格。
- 明确原始问题
- 递推关系建立
- 分析最优子结构
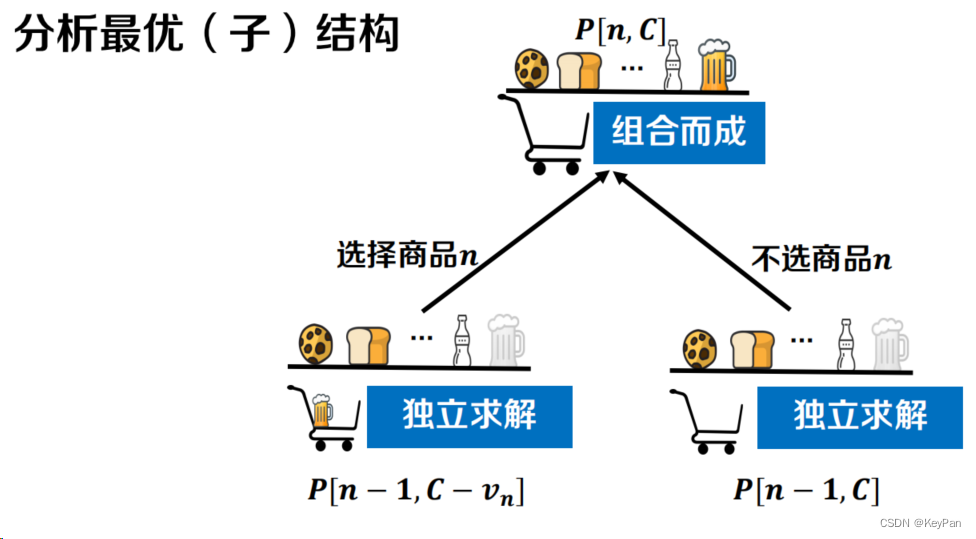
- 构造递推公式
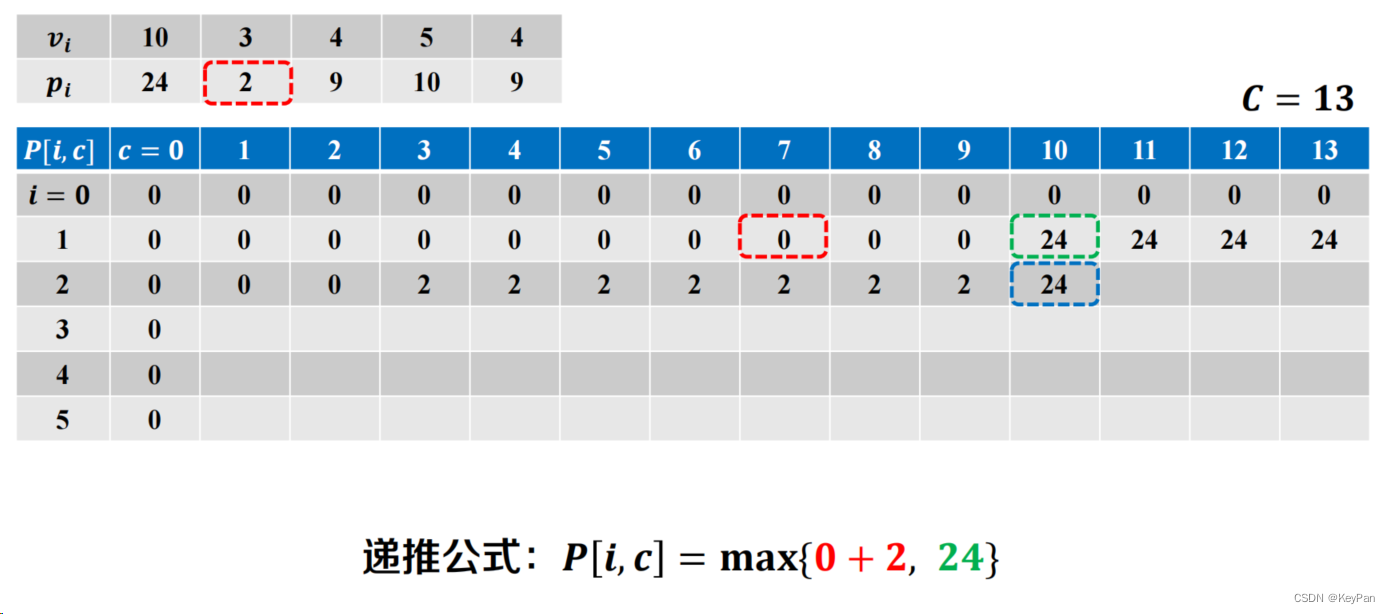
𝑷[𝒊, 𝒄] = 𝐦𝐚𝐱{𝑷[𝒊 − 𝟏, 𝒄] , 𝑷[𝒊 − 𝟏, 𝒄 − 𝒗𝒊] + 𝒑𝒊}
- 分析最优子结构
- 自底向上计算
- 确定计算顺序
-
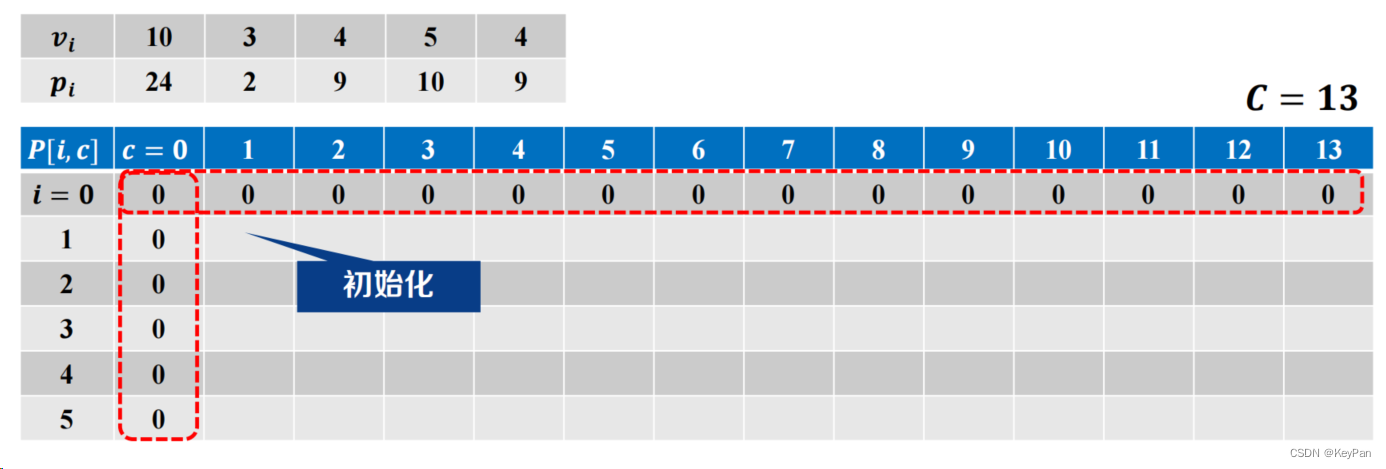
状态初始化
- 容量为0时:𝑷[𝒊, 𝟎] = 𝟎
- 没有商品时:𝑷[𝟎 , 𝒄] = 𝟎

-
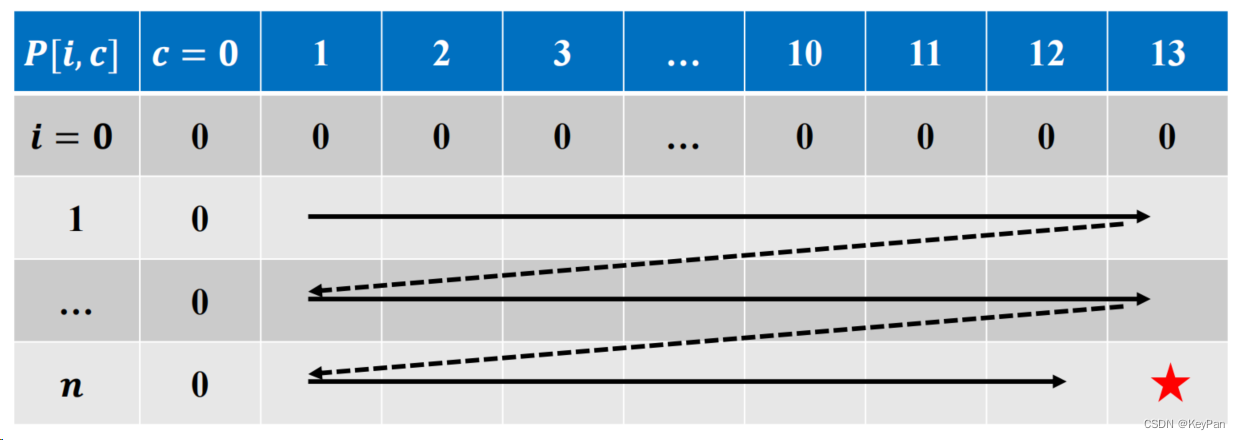
明确子问题依赖关系
𝑷[𝒊, 𝒄]依赖于子问题𝑷[𝒊 − 𝟏, 𝒄 − 𝒗𝒊]和𝑷[𝒊 − 𝟏, 𝒄]

-
计算顺序结果
-
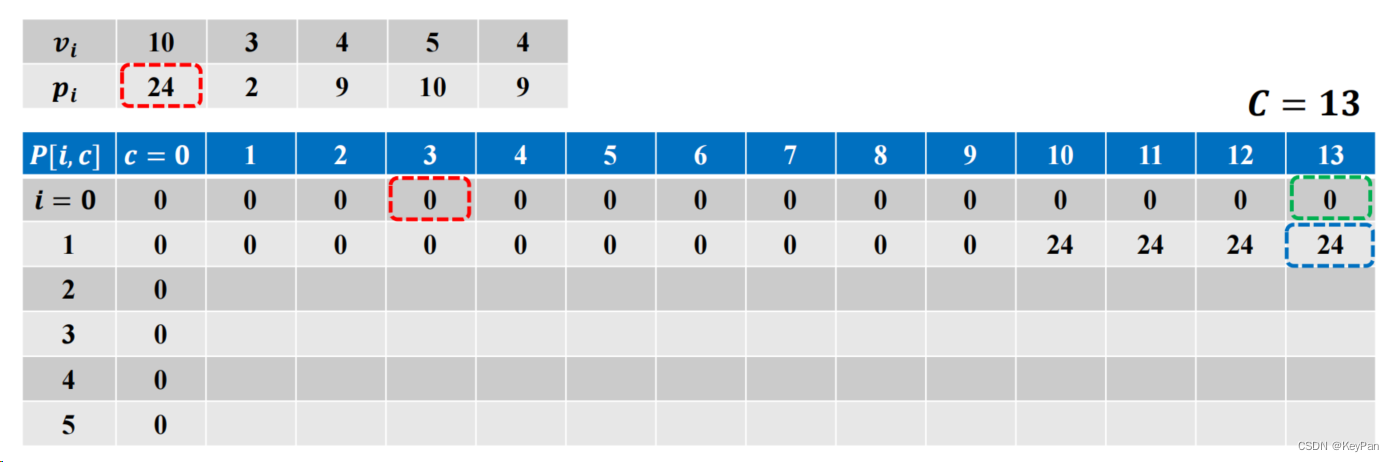
- 依次求解子问题
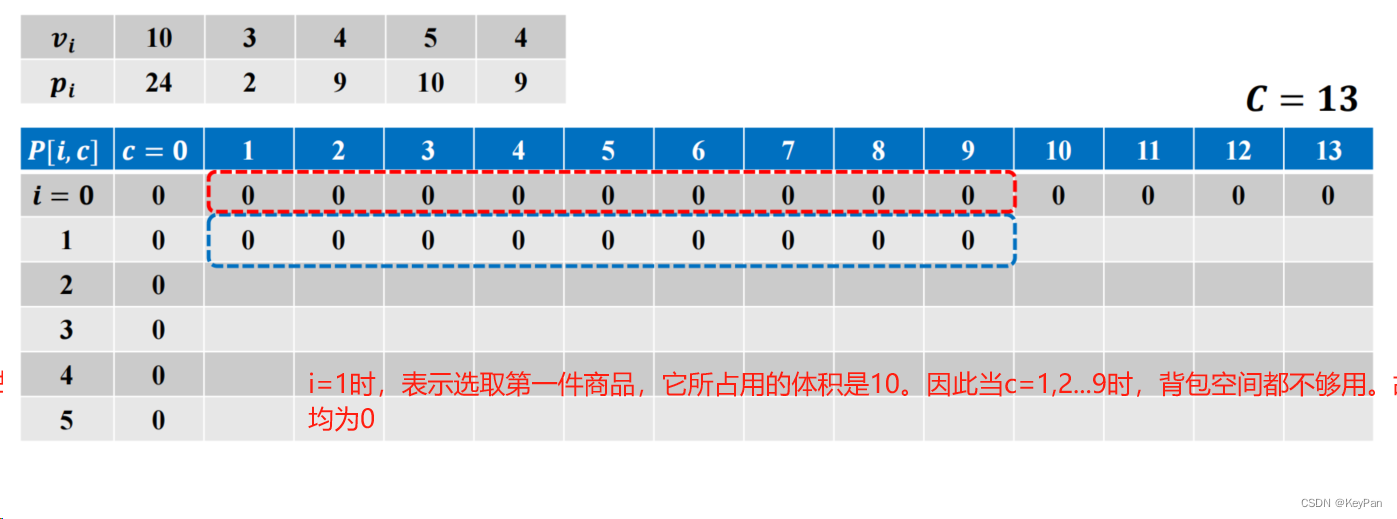

…
…

…
…
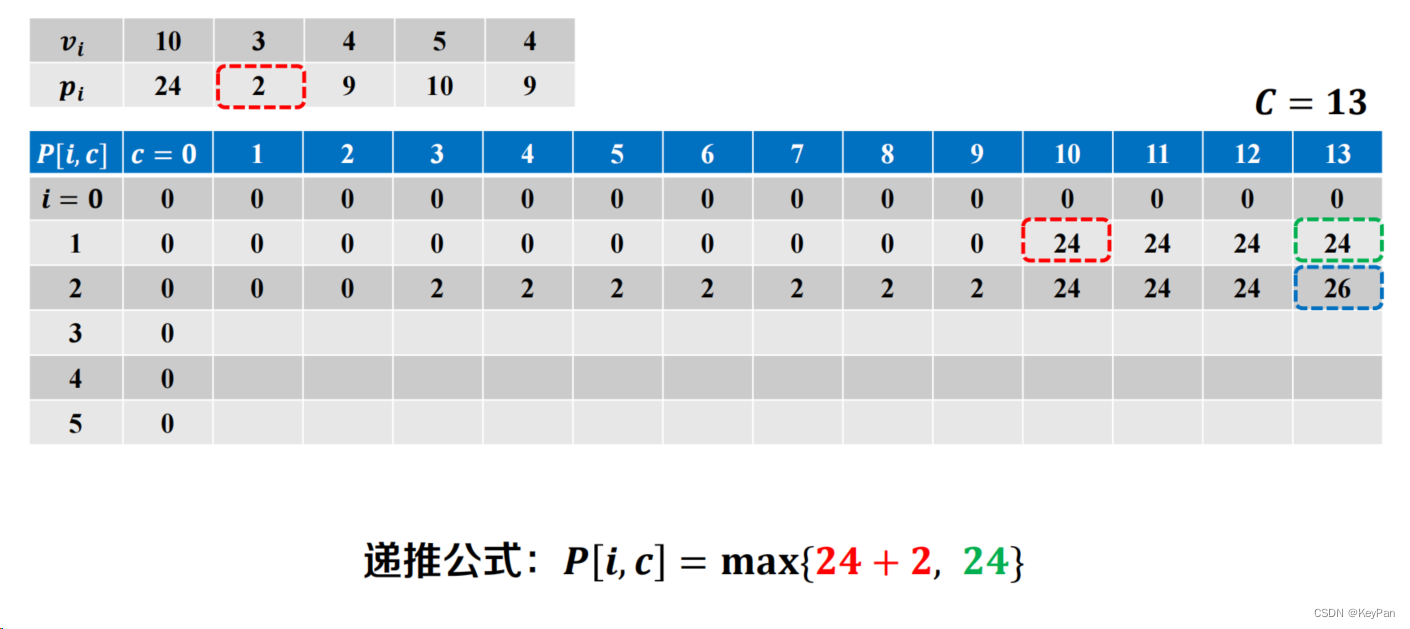
…以此类推
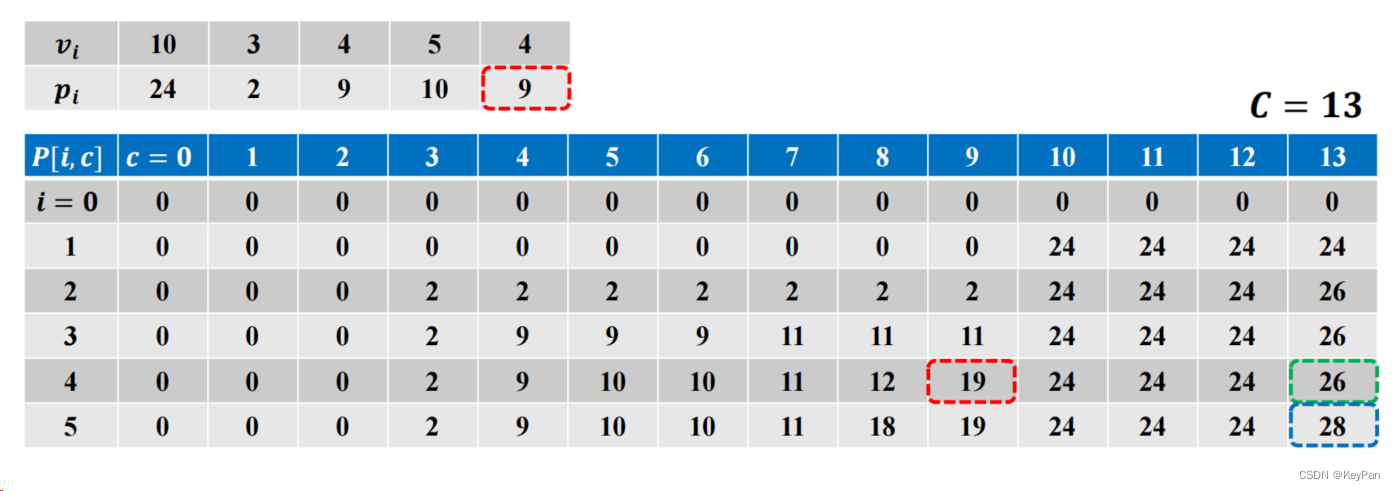
- 确定计算顺序
- 最优方案追踪
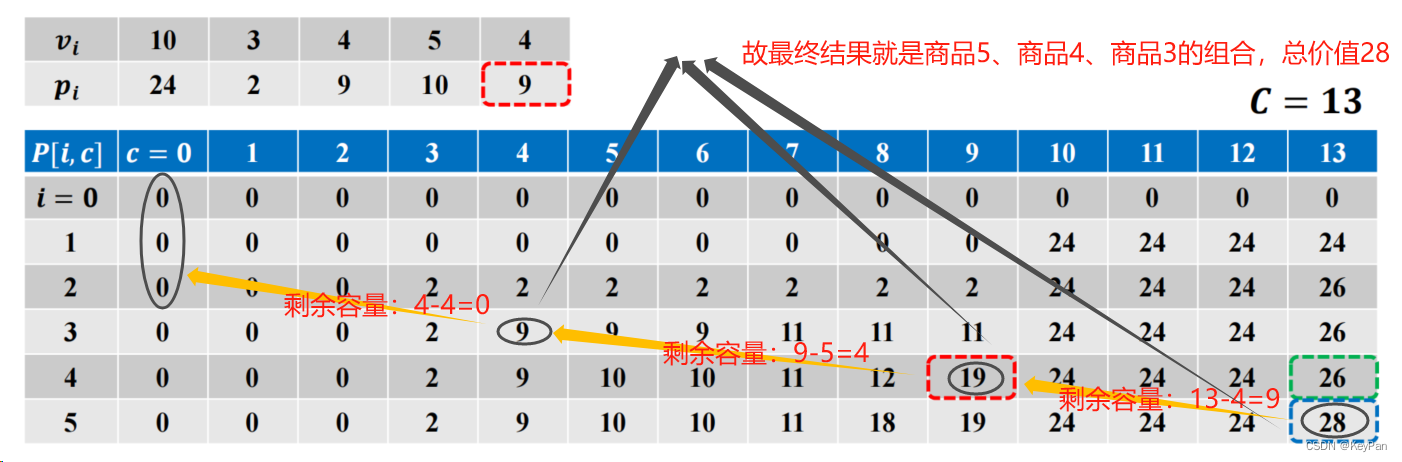
- 从总价值最大P[5,13]=28入手,28不等于P[4,13]=26,故第5个商品被选,剩余背包体积13-4=9。我没要看P[4,9]。
- P[4,9]=19不等于P[3,9]=11,故第4个商品被选,剩余背包体积9-5=4。我没要看P[3,4]。
- P[3,4]=9不等于P[2,4]=2,故第3个商品被选,剩余背包体积4-4=0。此时背包空间为0,追踪结束。
- 最终结果选了商品5、4、3。
算法性能
时间复杂度
在动态规划中,我们填充一个二维的 dp 表格,其中有 N 行(物品数量)和 W 列(背包容量)。每个单元格需要计算一次,而计算每个单元格的时间复杂度为常数时间。因此,0-1背包问题的动态规划算法的时间复杂度为 O(N*W)。
空间复杂度
动态规划算法需要一个二维数组来存储子问题的解,因此空间复杂度为 O(N*W)。这可能在某些情况下占用大量内存,特别是当物品数量和背包容量非常大时。
稳定性
检查算法在不同输入情况下的性能是否一致。算法应该对不同问题实例的输入数据表现稳定,而不会因输入的变化而导致不稳定的结果。
算法总结
总的来说,动态规划算法对于解决0-1背包问题是一种非常有效的方法,尤其适用于中小规模的问题。对于非常大的规模问题,时间和空间复杂度可能会变得不可行。因此在处理大规模问题时,需要谨慎考虑性能和可行性。算法的实际效果也受到问题特性和硬件环境的影响。




















 829
829











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








