阅读笔记 | Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting

阅读论文：

1. Wu, Haixu, et al. “Autoformer: Decomposition transformers with auto-correlation for long-term series forecasting.” Advances in neural information processing systems 34 (2021): 22419-22430.

背景与动机

由于难以捕捉时间序列本身的复杂时序模式，长期时序预测难以进行。而善于捕捉长序依赖的经典自注意力机制由于其平方计算复杂度而让人望而却步。为了发挥注意力机制的长序依赖建模能力，文章强调并解决了长期时序预测中，复杂时序模式难捕捉和注意力机制计算量大的问题。

模型

文章的模型整体结构参考了原始Transformer，采用了Encoder-Decoder结构。其中最为不同的是文章引入的两个block，分别用于应对背景中提出的两个主要问题。

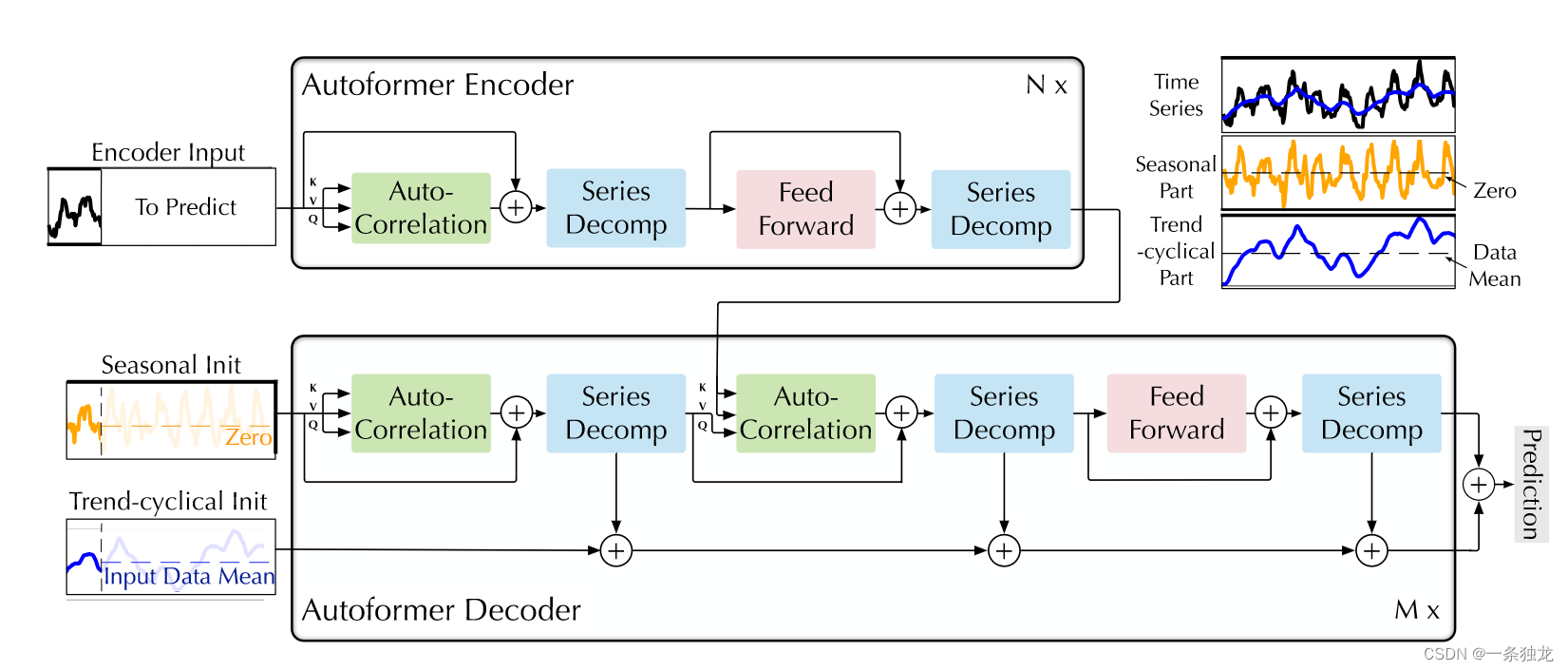
Encoder部分用于建模学习时序数据的季节性部分，最终Series Decomp block分解输出的趋势部分是被裁掉的，只有季节性部分输出到Decoder进行互相关计算。

Decoder部分对于周期分量使用自相关机制进行依赖建模，并聚合与相似过程的子序列；对于趋势分量，使用加权累积方式，逐步从预测的隐变量中提取出趋势信息。而最终的预测结果是由预测的趋势分量和季节性分量加权相加得到的。

$$\begin{array}{rl}{\mathcal{S}}_{\mathrm{de}}^{l,1},{\mathcal{T}}_{\mathrm{de}}^{l,1}& =\mathrm{SeriesDecomp}\left(\text{ Auto-Correlation }\left({\mathcal{X}}_{\mathrm{de}}^{l-1}\right)+{\mathcal{X}}_{\mathrm{de}}^{l-1}\right)\\ {\mathcal{S}}_{\mathrm{de}}^{l,2},{\mathcal{T}}_{\mathrm{de}}^{l,2}& =\mathrm{SeriesDecomp}\left(\text{ Auto-Correlation }\left({\mathcal{S}}_{\mathrm{de}}^{l,1},{\mathcal{X}}_{\mathrm{en}}^N\right)+{\mathcal{S}}_{\mathrm{de}}^{l,1}\right)\\ {\mathcal{S}}_{\mathrm{de}}^{l,3},{\mathcal{T}}_{\mathrm{de}}^{l,3}& =\mathrm{SeriesDecomp}\left(\text{ FeedForward }\left({\mathcal{S}}_{\mathrm{de}}^{l,2}\right)+{\mathcal{S}}_{\mathrm{de}}^{l,2}\right)\\ {\mathcal{T}}_{\mathrm{de}}^l& ={\mathcal{T}}_{\mathrm{de}}^{l-1}+{\mathcal{W}}_{l,1}\ast {\mathcal{T}}_{\mathrm{de}}^{l,1}+{\mathcal{W}}_{l,2}\ast {\mathcal{T}}_{\mathrm{de}}^{l,2}+{\mathcal{W}}_{l,3}\ast {\mathcal{T}}_{\mathrm{de}}^{l,3}\end{array}$$

针对复杂时序模式的捕捉，文章提到了时序分析中常用的时序分解思想，即，将单一的时序分解为多个更易于预测的子序列，然后再做注意力。为此引入Series Decomp模块，用以将时序数据分解为季节性分量和趋势-周期性分量（趋势和非季节导致的周期性的结合）。其分解方法比较简单，使用了基于平均池化操作的移动平均方法平滑掉周期性波动得到长期趋势。

$$\begin{array}{rl}& {\mathcal{X}}_{\mathrm{t}}=\mathrm{AvgPool}(\mathrm{Padding}(\mathcal{X}))\\ & {\mathcal{X}}_{\mathrm{s}}=\mathcal{X}-{\mathcal{X}}_{\mathrm{t}}\end{array}$$

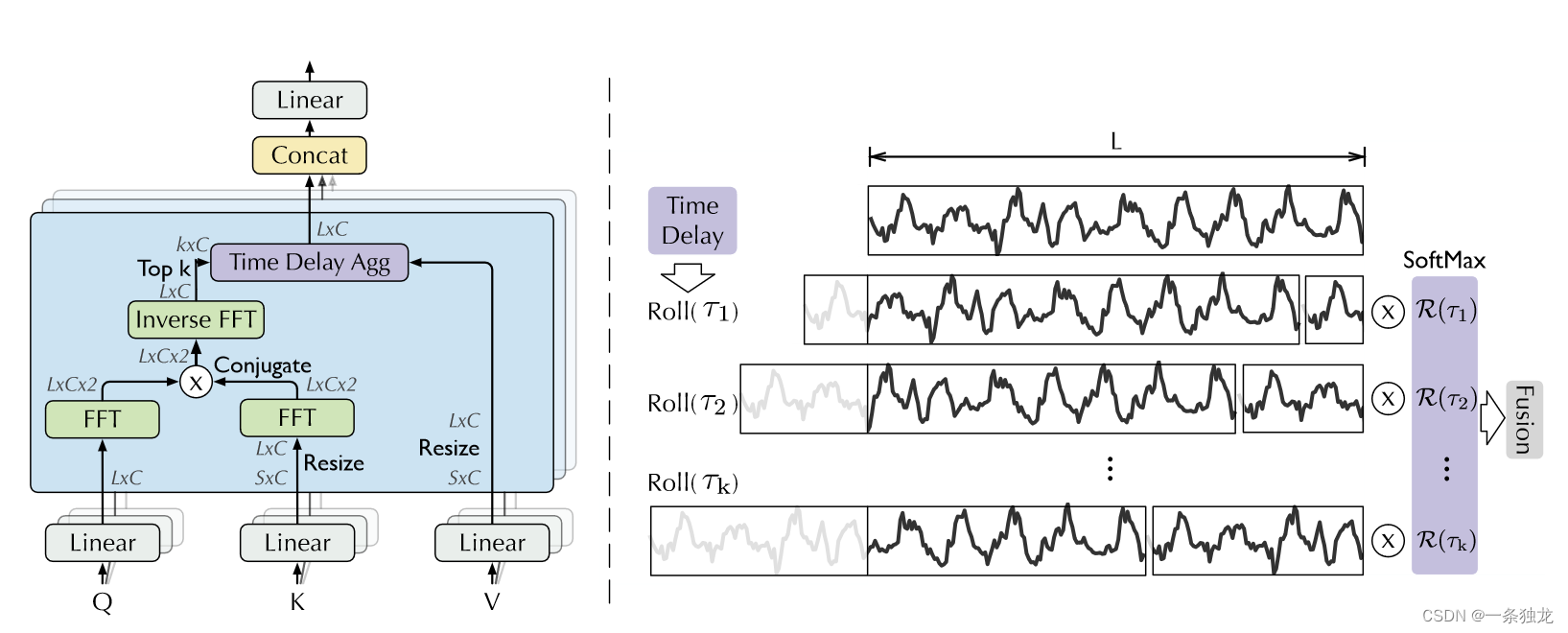
对于自注意力机制的计算复杂度问题，文章基于随机过程理论，用基于快速傅里叶变换的自相关性机制替代使用矩阵运算的自注意力机制，实现了 $\mathrm{O}(L\log L)$ 的计算复杂度。具体而言，文章观察到不同周期的相似相位间通常存在相似子过程，利用这种相似性设计了自相关机制。自相关性的计算定义和基于Wiener-Khinchin理论用快速傅里叶变换实现的$\tau$步滞后时序自相关性计算公式下：

$${\mathcal{R}}_{\mathcal{XX}}(\tau )=\underset{L\to \infty }{\lim }\frac{1}{L}\sum _{t=1}^L{\mathcal{X}}_t{\mathcal{X}}_{t-\tau }$$

$$\begin{array}{rl}& {\mathcal{S}}_{\mathcal{XX}}(f)=\mathcal{F}\left({\mathcal{X}}_t\right){\mathcal{F}}^{\ast }\left({\mathcal{X}}_t\right)={\int }_{-\infty }^{\infty }{\mathcal{X}}_t{e}^{-i2\pi tf}\mathrm{d}t{\int }_{-\infty }^{\infty }{\mathcal{X}}_t{e}^{-i2\pi tf}\mathrm{d}t\\ & {\mathcal{R}}_{\mathcal{XX}}(\tau )={\mathcal{F}}^{-1}\left({\mathcal{S}}_{\mathcal{XX}}(f)\right)={\int }_{-\infty }^{\infty }{\mathcal{S}}_{\mathcal{XX}}(f)e^{i2\pi f\tau }\mathrm{d}f\end{array}$$

这种时延相似性结果可以看做周期为$\tau$置信度为${\mathcal{R}}_{\mathcal{XX}}(\tau )$，也就是实现了对序列的周期长度进行了估计。为了实现不同周期的相似性结果在序列级进行连接，文章设计了时延信息聚合。首先对于序列的不同周期的估计根据置信度排序，选取置信度最高的$k$个周期，再对这些相似性结果组成的序列做softmax后与其本向前滚动$\tau$步对齐后的结果相乘再进行求和。

τ 1 , ⋯   , τ k = arg ⁡ Topk ⁡ τ ∈ { 1 , ⋯   , L } ( R Q , K ( τ ) ) R ^ Q , K ( τ 1 ) , ⋯   , R ^ Q , K ( τ k ) = S o f t Max ⁡ ⁡ ( R Q , K ( τ 1 ) , ⋯   , R Q , K ( τ k ) )  Auto-Correlation  ( Q , K , V ) = ∑ i = 1 k Roll ⁡ ( V , τ i ) R ^ Q , K ( τ i ) \begin{aligned} \tau_1, \cdots, \tau_k & =\underset{\tau \in\{1, \cdots, L\}}{\arg \operatorname{Topk}}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}(\tau)\right) \\ \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right) & =\operatorname{Soft\operatorname {Max}}\left(\mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_1\right), \cdots, \mathcal{R}_{\mathcal{Q}, \mathcal{K}}\left(\tau_k\right)\right) \\ \text { Auto-Correlation }(\mathcal{Q}, \mathcal{K}, \mathcal{V}) & =\sum_{i=1}^k \operatorname{Roll}\left(\mathcal{V}, \tau_i\right) \widehat{\mathcal{R}}_{\mathcal{Q}, \mathcal{K}}\left(\tau_i\right) \end{aligned} τ1​,⋯,τk​R Q,K​(τ1​),⋯,R Q,K​(τk​) Auto-Correlation (Q,K,V)​=τ∈{1,⋯,L}argTopk​(RQ,K​(τ))=SoftMax(RQ,K​(τ1​),⋯,RQ,K​(τk​))=i=1∑k​Roll(V,τi​)R Q,K​(τi​)​

实验

• 数据集

  • ETT：采样间隔15分钟的电力负荷和油温

  • Electricity：小时级别的用户用电

  • Exchange：日级别的货币汇率

  • Traffic：小时级别的道路占用率

  • Weather：采样间隔10分钟21种气象指标的天气数据

  • ILI：星期级的流感样疾病患病人数

• 指标

  • MSE

  • MAE

• Baselines

  • 多变量

    • Informer

    • Reformer

    • LogTrans

    • LSTNet

    • LSTM

    • TCN

  • 单变量

    • Informer

    • Reformer

    • LogTrans

    • N-BEATS

    • DeepAR

    • Prophet

    • ARMIA

• 实验设置：在单变量和多变量数据下，对于同一数据集均进行不同长度的预测，计算指标进行对比。并对本文方法进行消融实验。

• 实验结果：对比实验表明Autoformer在多领域数据的多输入输出长度设置下一致取得SOTA，且预测结果长度越长，提升更明显；消融实验表明本文方法的自相关机制可以正确发现每个周期的下降过程，并展现出明显的时间效率和内存占用上的提升。

个人思考

• 信号分析手段的引入：时序分解中，时序数据可进行季节性、趋势和差分等方面的分解。在季节性分解中，还经常用到小波分解或是傅立叶分解等信号分析手段。特别地，小波分解相对傅里叶变换提供了更好的局部化特性，相当于为时序打造的放大镜，可以更精细地捕捉短期和局部的变化。将更多信号分析手段引入时序数据分析中是有很多好处的，不光是可以对时序数据分解为深度学习模型更易于建模预测的分量，还可以利用信号处理手段对数据进行降噪等处理（类比本文将时序分解的操作从只在预处理阶段进行提升到可以自由安排执行，提供更多灵活性），并在分量分解上提供一定的可解释性（比如提供物理上的解释）。
• 自相关性与互相关性计算：传统时序分析里的相关性分析是非常重要的一步，时序数据的滞后自相关性可以发现其时序依赖关系，而互相关性分析可以发现时序数据与其它变量间存在的关系。本文中强调了时序数据本身的自相关性计算，但似乎并未强调多变量时序预测下时序数据与其它变量间的互相关性计算，特别是其它变量中包含离散变量的情况下。