最小割最大流 Minimum Cut-Max Flow/图割 Graph Cut的理解

• 最小割（Minimum Cut）

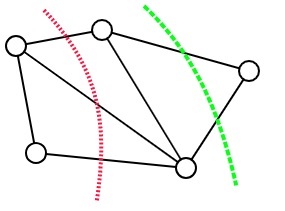
在图论中，图的最小割是划分两个不相交的子集时，所割掉的边为最小，如绿色的线：

具体的例子：

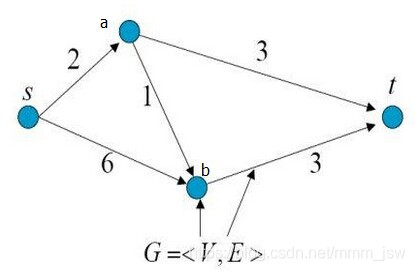
从s点到t点有三条路径：

s --> a --> t;

s --> a --> b --> t;

s --> b --> t.

现要求在保证所剪去边的权重最小的情况下，使得s --> t 的路径不存在。答案是剪去s --> a (2) 和 b --> t (3) 两条边，这种方法称为最小割。

 

• 最大流 （Max Flow）

假设从点s有源源不断的水流出，将每条边为能通过的最大水量，例如s --> a 最大的水量为2，最后点t能接受的水流量是多少？

s --> a --> t; （2）

s --> a --> b --> t; （0，和其他两条路重复）

s --> b --> t. （3）

最后流入的水流量也为5。

 

• 证明最大流问题 == 最小流问题

（1）最大割可能大于最小流吗？

（2）最大割可能小于最小流吗？

 

• GraphCut

GraphCut利用最小割最大流算法进行图像的分割，使用时需要给定前景和背景的点（种子，seed）作为输入，算法将建立各个像素点与前景和背景相似度的赋权图，然后通过最小割最大流区分前景和背景。