AL-iLQR

Objective

状态微分方程，$x$是状态量，$u$是控制量，$\dot{x}$是对时间的微分。

轨迹优化问题的目标：（连续）

$l(x(t_f))$指的是$t_f$时刻的状态到终点状态的cost（比如距终点的距离），${\int }_0^{t_f}l(x(t),u(t))$是从0到$t_f$时刻累计的过程成本（比如里程数、耗油量等）。轨迹优化问题致力于着有效的方式去解决差分约束优化问题。
进行离散化，差分方程

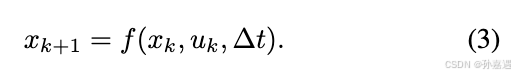
目标改写成：

求解方法

1、直接法

直接方法将状态和控制视为决策变量，并使用通用非线性规划 (NLP) 求解器，例如 SNOPT 或 IPOPT。这些方法通常将优化问题转化为 (4) 中给出的形式的某些内容，通常具有不同的方法来逼近连续时间动力学或问题约束的独特公式。最常见的方法，direct collocation(DIRCOL, 配点法)，使用 Hermite-Simpson 积分来整合cost和动力学，这本质上是状态的三阶隐式 Runge-Kutta 积分器和控制量的一阶保持（即线性插值）。这些方法直接受益于它们所依赖的 NLP 求解器的鲁棒性和通用性。然而，直接方法也往往相当慢，需要大型优化包。
直接配点法的学习详见：

2、间接法

严格遵循（4）的马尔可夫结构，然后通过模拟系统的动力学来隐式强制执行动力学约束。差分动态规划 (DDP) 和迭代 LQR (iLQR) 是密切相关的间接法，通过把问题分解为多个子问题。
DDP 方法通过在每个时间步的动态前向模拟期间合并反馈策略来改进更幼稚的“simple shooting”方法。由于其对动态可行性的严格执行，通常很难找到为 DDP 方法生成合理初始化的控制序列。虽然它们速度很快，内存占用较低，这使得它们易于嵌入式实现，但 DDP 方法历来被认为在数值上不太稳健，不太适合处理非线性状态和输入约束。

3、本教程 AL-iLQR Tutorial

本教程推导了在增广拉格朗日框架内使用DDP或iLQR求解约束轨迹优化问题的方法。结果是一种快速、高效的算法，允许对状态和控制进行非线性相等和不等式约束。

背景知识

增广拉格朗日

增广拉格朗日一般用于解决带有约束的优化问题：
解决带有约束的问题一般是降约束放入cost函数，并且迭代的增加接近或违反约束的惩罚。一般会在惩罚接近于无穷大的时候收敛到最优解，但是这对数值计算是不切实际的。所以增广拉格朗日方法通过保持与约束相关的的拉格朗日乘子的估计来改进惩罚方法。

$\lambda$是拉格朗日乘子，$\mu$是惩罚乘子，当满足约束并且拉格朗日乘子为0时，$I_{\mu }=0$，否则为惩罚乘子。

问题求解：1）$\lambda$和$\mu$初始都是固定常数。2）更新拉格朗日乘子，当这次迭代满足约束等式和满足约束不等式使用不同的更新策略。3）更新惩罚乘子，一般$\varphi \in (2,10)$。4）是否收敛。 5）不满足的话继续迭代

Linear Quadratic Regular (LQR)

1、objective

$R$是实对称正定矩阵，$Q$是实对称半正定矩阵。（因为是线性控制）

2、连续LQR（HJB方程）

$t_f$时刻的成本函数：

最小cost：（这个一般也是值函数）

定义的Hamiltonian（最小cost $J$的一阶偏微分方程）: $l(x(t),u(t)$是当前时刻过程成本，$J_x^{\ast }=\frac{\partial J^{\ast }}{\partial x}$， $f(x(t),u(t),t)$是动力学（微分状态方程）

Hamilton-Jacobi-Bellman 方程（HJB)
实际上是从一阶泰勒展开来的，
如果是LQR的话，$\frac{\partial H}{\partial u}=0$


代入回Hamiltonian，
假设最小cost是二次型：$K$需要是对称正定的
代入回HJB方程

利用二次型的对称性以及对所有 $x(t)$都为0，得到Riccati方程：
使用求解器（LQR和卡尔曼滤波都经常使用对偶的riccati方程），得到控制策略

3、离散LQR

同样是构建HJB方程，不赘述了。需要注意的是是从后往前进行的推导，这是边界条件：

AL-DDP

动态规划的关键思想是在每次迭代中，所有的非线性约束和objectives都使用一阶或者二阶泰勒展开来近似，以便于用离散LQR进行求解。最优反馈策略是在后项传播（backward pass)中进行计算的，因为ddp是从轨迹的尾部开始。然后最优的推进作用在前向的轨迹规划中。

为了处理约束，我们简单地用增广拉格朗日的乘数和惩罚项“增广”代价函数，将λ和μ视为常数。经过多次迭代DDP后，更新乘子和惩罚项。

Backward Pass

就是之前的值函数加上约束，$V_k(x){|}_{\lambda ,\mu }$ 是使用拉格朗日乘子和惩罚项估计的在第k步耗费的过程成本。

对其进行二阶泰勒展开
就像公式（28）一样，最后一步不需要优化控制量：