双重差分模型
定义
双重差分法(Difference in Differences): 通过利用观察学习的数据,计算自然实验中“实验组”与“对照组”在干预下增量的差距。

步骤:
- 分组:对于一个自然实验,其将全部的样本数据分为两组:一组是受到干预影响,即实验组;另一组是没有受到同一干预影响,即对照组;
- 目标选定:选定一个需要观测的目标指标,如购买转化率、留存率,一般是希望提升的KPI;
- 第一次差分:分别对在干预前后进行两次差分(相减)得到两组差值,代表实验组与对照组在干预前后分别的相对关系;
- 第二次差分:对两组差值进行第二次差分,从而消除实验组与对照组原生的差异,最终得到干预带来的净效应。
参考【传送门】

δ ^ = ( y ˉ T , 1 − y ˉ T , 0 ) − ( y ˉ C , 1 − y ˉ C , 0 ) \hat{\delta}=\left(\bar{y}_{T, 1}-\bar{y}_{T, 0}\right)-\left(\bar{y}_{C, 1}-\bar{y}_{C, 0}\right) δ^=(yˉT,1−yˉT,0)−(yˉC,1−yˉC,0)
实验组干预前后的均值的差减去对照组干预前后均值的差
理解
1.在一些论文报告中,有一个DID的变量,可以看下面这个例子理解。

就是个体(时间)与政策虚拟变量的乘积。
stata实现

gen gd=t*treated
reg fte gd treated t bk kfc roys,r
diff fte, t(treated) p(t) cov(bl kfc roys) robust
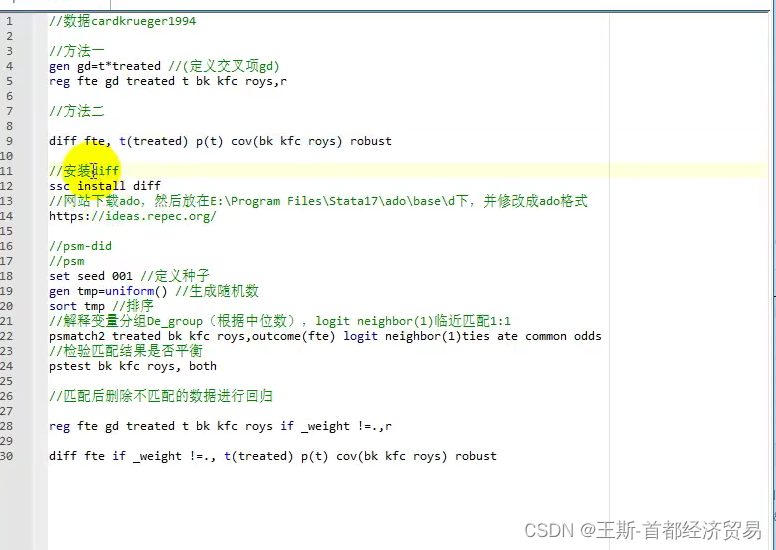
一般情形下:是先做PSM倾向性得分匹配
答:因为在研究某一政策的影响时,可能还包含其他的政策影响因素,PSM的目的是为了去掉其他的干扰。







 双重差分模型(DID)是一种统计方法,用于评估政策或干预措施的效果。它通过比较实验组和对照组在干预前后的变化来消除固有差异,计算出净效应。DID涉及到分组、选择目标指标、两次差分步骤,并且在实际应用中常与PSM(倾向性得分匹配)结合,以减少其他因素的影响。
双重差分模型(DID)是一种统计方法,用于评估政策或干预措施的效果。它通过比较实验组和对照组在干预前后的变化来消除固有差异,计算出净效应。DID涉及到分组、选择目标指标、两次差分步骤,并且在实际应用中常与PSM(倾向性得分匹配)结合,以减少其他因素的影响。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










