概率与统计样卷一

试卷一

一、填空（每小题2分，共10分）

１．设是三个随机事件，则至少发生两个可表示为______________________。

２. 掷一颗骰子，表示“出现奇数点”，表示“点数不大于3”，则表示______________________。

３．已知互斥的两个事件满足，则___________。

４．设为两个随机事件，，，则___________。

５．设是三个随机事件，，，、，则至少发生一个的概率为___________。

 

二、单项选择（每小题的四个选项中只有一个是正确答案，请将正确答案的番号填在括号内。每小题2分，共20分）

1. 从装有2只红球，2只白球的袋中任取两球，记“取到2只白球”，则（     ）。

(A) 取到2只红球                           (B) 取到1只白球

(C) 没有取到白球                          (D) 至少取到1只红球

2．对掷一枚硬币的试验, “出现正面”称为（     ）。

(A) 随机事件                              (B) 必然事件

(C) 不可能事件                            (D) 样本空间

3. 设A、B为随机事件，则（     ）。

(A)  A                              (B)  B           

(C)  AB                             (D)  φ

4. 设和是任意两个概率不为零的互斥事件，则下列结论中肯定正确的是（     ）。

(A)  与互斥                          (B) 与不互斥

(C)               (D)

5. 设为两随机事件，且，则下列式子正确的是（     ）。

(A)                    (B)

(C)                     (D)      

6. 设相互独立，则（     ）。

(A)                                    (B)

(C)                                   (D)

7.设是三个随机事件，且有，则（     ）。

(A) 0.1                                  (B) 0.6

(C) 0.8                                  (D)0.7

8. 进行一系列独立的试验，每次试验成功的概率为p，则在成功2次之前已经失败3次的概率为（     ）。

(A)  p^2(1– p)^3                         (B)  4p(1– p)^3         

 (C)  5p^2(1– p)^3                       (D)  4p^2(1– p)^3  

9. 设A、B为两随机事件，且，则下列式子正确的是（     ）。

(A)                (B)

(C)                  (D)

10. 设事件A与B同时发生时，事件C一定发生，则（     ）。

(A)  P(A B) = P (C)                    (B)  P (A) + P (B) – P (C) ≤ 1

(C)  P (A) + P (B) – P (C) ≥ 1          (D)  P (A) + P (B) ≤ P (C)

三、计算与应用题（每小题8分，共64分）

1. 袋中装有5个白球，3个黑球。从中一次任取两个。

求取到的两个球颜色不同的概率。

 

2. 10把钥匙有3把能把门锁打开。今任取两把。

求能打开门的概率。

 

3. 一间宿舍住有6位同学，

求他们中有4个人的生日在同一个月份概率。

 

4. 50个产品中有46个合格品与4个次品，从中一次抽取3个，

求至少取到一个次品的概率。

 

5. 加工某种零件，需经过三道工序，假定第一、二、三道工序的次品率分别为0.2，0.1，0.1，并且任何一道工序是否出次品与其它各道工序无关。

求该种零件的次品率。

 

6. 已知某品的合格率为0.95，而合格品中的一级品率为0.65。

求该产品的一级品率。

 

7. 一箱产品共100件,其中次品个数从0到2是等可能的。开箱检验时，从中随机抽取10件，如果发现有次品，则认为该箱产品不合要求而拒收。若已知该箱产品已通过验收，

求其中确实没有次品的概率。

 

8. 某厂的产品，按甲工艺加工，按乙工艺加工，两种工艺加工出来的产品的合格率分别为0.8与0.9。现从该厂的产品中有放回地取5件来检验，

求其中最多有一件次品的概率。

 

四、证明题（共6分）

设，。证明：

 

 

 

试卷一  

参考答案

一、填空

1.  或

2. 出现的点数恰为5

3.

与互斥

  则

4. 0.6

故 

5.

至少发生一个，即为

又由  得

故

 

二、单项选择

1．

2. A

3. A

  利用集合的运算性质可得.

4．

与互斥

故 

5．

故

6．

相互独立

7.

 且

则

8.  

9. B

10. B

故  P (A) + P (B) – P (C) ≤ 1

三、计算与应用题

1. 解：

设 表示“取到的两球颜色不同”，则

而样本点总数

故

2. 解：

设 表示“能把门锁打开”，则，而

故

3. 解：

设 表示“有4个人的生日在同一月份”，则

而样本点总数为

故

4. 解：

设 表示“至少取到一个次品”，因其较复杂，考虑逆事件=“没有取到次品”

则 包含的样本点数为。而样本点总数为

故

5. 解：

设 “任取一个零件为次品”

由题意要求，但较复杂，考虑逆事件“任取一个零件为正品”，表示通过三道工序都合格，

则

于是

6. 解：

设 表示“产品是一极品”，表示“产品是合格品”

显然，则

于是

即 该产品的一级品率为

7. 解：

设 “箱中有件次品”，由题设，有

又设 “该箱产品通过验收”，由全概率公式，有

于是

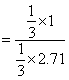
8. 解：

依题意，该厂产品的合格率为，

于是，次品率为

设 表示“有放回取5件，最多取到一件次品”

则

 

四、证明题

证明

 ，  ，

由概率的性质知      则

又   

且 

故