调用matlab曲线拟合工具箱，自定义函数预测人口数量

好的！文西

已于 2022-09-25 21:34:48 修改

阅读量5.9k

点赞数 4

分类专栏： Matlab 数模文章标签：拟合曲线 matlab

于 2022-09-25 21:31:07 首次发布

本文链接：https://blog.csdn.net/weixin_43275631/article/details/127042723

版权

Matlab 同时被 2 个专栏收录

14 篇文章

订阅专栏

数模

5 篇文章

订阅专栏

拟合所求函数值不需要在已知点精确等于原始函数值，目的为了使用更简单的函数更低次的多项式表示原函数。相比插值，面对大量节点情况下选择拟合求函数曲线不失为一种更好的方法，拟合得到的曲线为一条确定的曲线。

现有一组数据分布如下图：

我们要求一条直线/曲线（高次多项式方法）进行表示y与x之间的关系假设该拟合曲线为:

$y=k x+b$

求解该曲线即求各样本点与曲线距离的最小值时的k b值，表达式：

$\hat{y}_i=k x_i+b$

$\hat{k}, \hat{b}=\underset{k, b}{\arg \min }\left(\sum_{i=1}^n\left(y_i-\hat{y}_i\right)^2\right)$

不用绝对值（绝对值不方便求导）、不用三次方（存在误差正负抵消的情况不满足目的）、不用四次方（避免极端数据对拟合曲线的影响）

令： $L=\sum_{i=1}^n\left(y_i-k x_i-b\right)^2$

现在要找k b使L最小，即令L对k、b求偏导，当偏导为0时解得的k b即为所需的值，计算公式如下：

$\left\{\begin{array} { l } { \frac { \partial L } { \partial k } = - 2 \sum _ { i = 1 } ^ { n } x _ { i } ( y _ { i } - k x _ { i } - b ) = 0 } \\ { \frac { \partial L } { \partial b } = - 2 \sum _ { i = 1 } ^ { n } ( y _ { i } - k x _ { i } - b ) = 0 } \end{array} \Rightarrow \left\{\begin{array}{l} \sum_{i=1}^n x_i y_i=k \sum_{i=1}^n x_i^2+b \sum_{i=1}^n x_i \\ \sum_{i=1}^n y_i=k \sum_{i=1}^n x_i+b n \end{array}\right.\right.$

$\Rightarrow\left\{\begin{array}{l} n \sum_{i=1}^n x_i y_i=k n \sum_{i=1}^n x_i^2+b n \sum_{i=1}^n x_i \\ \sum_{i=1}^n y_i \sum_{i=1}^n x_i=k \sum_{i=1}^n x_i \sum_{i=1}^n x_i+b n \sum_{i=1}^n x_i \end{array}\right.$

$n \sum_{i=1}^n x_i y_i-\sum_{i=1}^n y_i \sum_{i=1}^n x_i=k n \sum_{i=1}^n x_i^2-k \sum_{i=1}^n x_i \sum_{i=1}^n x_i \Rightarrow \hat{k}=\frac{n \sum_{i=1}^n x_i y_i-\sum_{i=1}^n y_i \sum_{i=1}^n x_i}{n \sum_{i=1}^n x_i^2-\sum_{i=1}^n x_i \sum_{i=1}^n x_i}$

同理计算得到

$\hat{b}=\frac{\sum_{i=1}^n x_i^2 \sum_{i=1}^n y_i-\sum_{i=1}^n x_i \sum_{i=1}^n x_i y_i}{n \sum_{i=1}^n x_i^2-\sum_{i=1}^n x_i \sum_{i=1}^n x_i}$

下面使用该公式计算拟合曲线的k b代码如下：

load data.mat
plot(x,y,'o');
xlabel('x的值');
ylabel('y的值');
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x));
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x));
hold on;
grid on;%显示网格线
xx = 2.5:0.1:7;
yy = k*xx+b;
plot(xx,yy,'-');

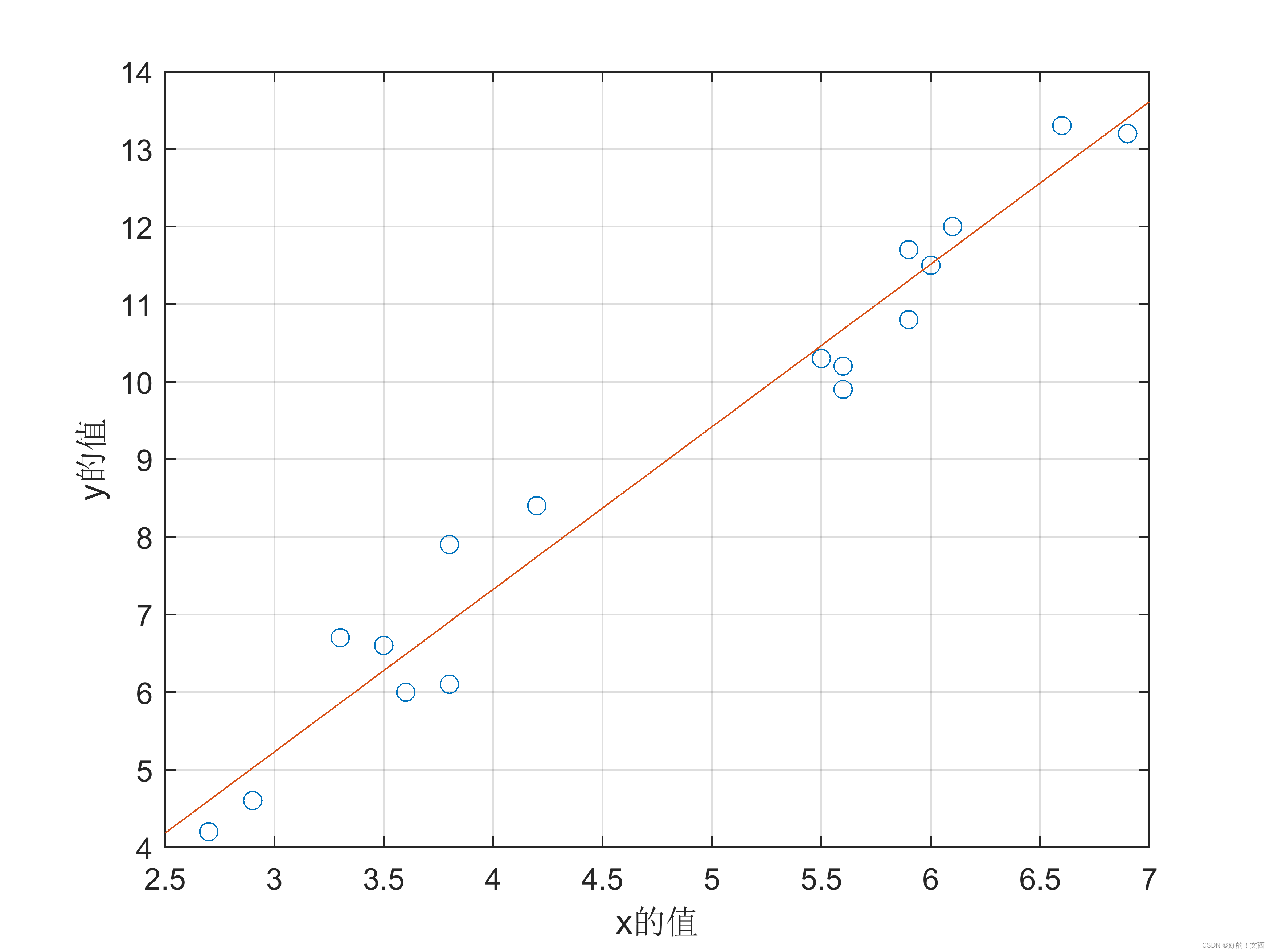
结果如下图：

下面使用matlab自带的曲线拟合工具箱根据以往数据预测后30年人口数量，

首先导入数据绘制出1790-2000年的人口变化predict_population.m：

%导入数据
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
plot(year,population,'o');

运行代码 :cftool调出工具箱如下图：

拟合方程出有很多方式可以选择，这里我们选择Custom Equation，在下方输入自己设定的函数：

$x(t)=\frac{x_m}{1+\left(\frac{x_m}{3.9}-1\right) e^{-r(t-1790)}}$

其中 $x_m$ 和 $r$ 是两个拟合参数，Results处显示拟合结果，其中r = 0.02735 xm = 342.4。按上图指示获取matlab自动生成的代码，并保存到本地。这里自动保存为createFit.m文档，在别的文档直接调用函数即可，在predict_population.m运行代码 [fitresult, gof] = createFit(year, population)显示结果如下图：

在得到拟合参数的基础上我们预测后30年的人口数据，代码如下：

%导入数据
year = 1790:10:2000;
population = [3.9,5.3,7.2,9.6,12.9,17.1,23.2,31.4,38.6,50.2,62.9,76.0,92.0,106.5,123.2,131.7,150.7,179.3,204.0,226.5,251.4,281.4];
t = 2001:2030;
xm = 342.4;   
r =  0.02735;
predictions = xm./(1+(xm./3.9-1).*exp(-r.*(t-1790)));  % 计算预测值（注意这里要写成点乘和点除,这样可以保证按照对应元素进行计算）
figure(2)
plot(year,population,'o',t,predictions,'.')  % 绘制预测结果图

结果如下图：