首先介绍一下绕三个坐标轴旋转一定角度需要的矩阵,后面计算时要用到,这里设旋转角度为θ
三维坐标系下
绕z轴旋转θ的矩阵Rz(θ)
{
c
o
s
θ
−
s
i
n
θ
0
0
s
i
n
θ
c
o
s
θ
0
0
0
0
1
0
0
0
0
1
}
\left\{ \begin{matrix} cosθ& -sinθ & 0& 0\\ sinθ & cosθ & 0& 0\\ 0 & 0 & 1 &0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧cosθsinθ00−sinθcosθ0000100001⎭⎪⎪⎬⎪⎪⎫
绕x轴旋转θ的矩阵Rx(θ)
{
1
0
0
0
0
c
o
s
θ
−
s
i
n
θ
0
0
s
i
n
θ
c
o
s
θ
0
0
0
0
1
}
\left\{ \begin{matrix} 1& 0 & 0& 0\\ 0 & cosθ & -sinθ& 0\\ 0 & sinθ&cosθ&0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧10000cosθsinθ00−sinθcosθ00001⎭⎪⎪⎬⎪⎪⎫
绕y轴旋转θ的矩阵Ry(θ)
{
c
o
s
θ
0
s
i
n
θ
0
0
1
0
0
−
s
i
n
θ
0
c
o
s
θ
0
0
0
0
1
}
\left\{ \begin{matrix} cosθ& 0 & sinθ& 0\\ 0 & 1 & 0& 0\\ -sinθ & 0&cosθ&0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧cosθ0−sinθ00100sinθ0cosθ00001⎭⎪⎪⎬⎪⎪⎫
绕任意轴旋转的计算的基本思想与二维平面下图像绕任意点旋转类似:
如下图,假设一图形绕P1P2所在的任意轴旋转角度θ,将任意轴经过一步步旋转、变换到旋转轴为z轴后再绕z轴进行旋转θ,最后再经矩阵逆变换到原来的位置。

步骤如下:

主要介绍Step1—>Step2—>Step3的内容包括:
1.求出P1P2直线的单位向量u(a,b,c),设P1(x1,y1,z1)P2(x2,y2,z2)直线为V轴:
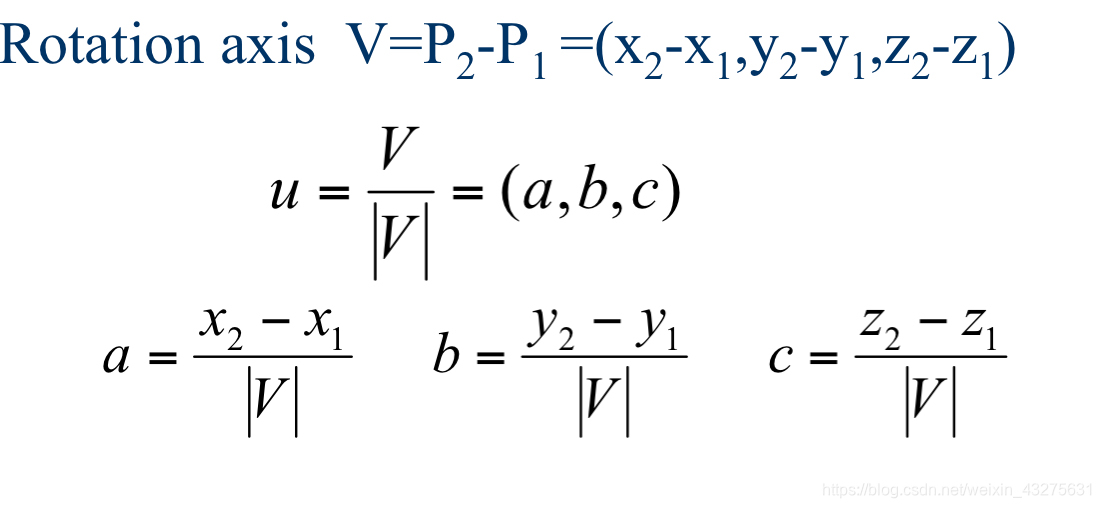
2.设置转换矩阵,将P1P2移动到原点坐标处:
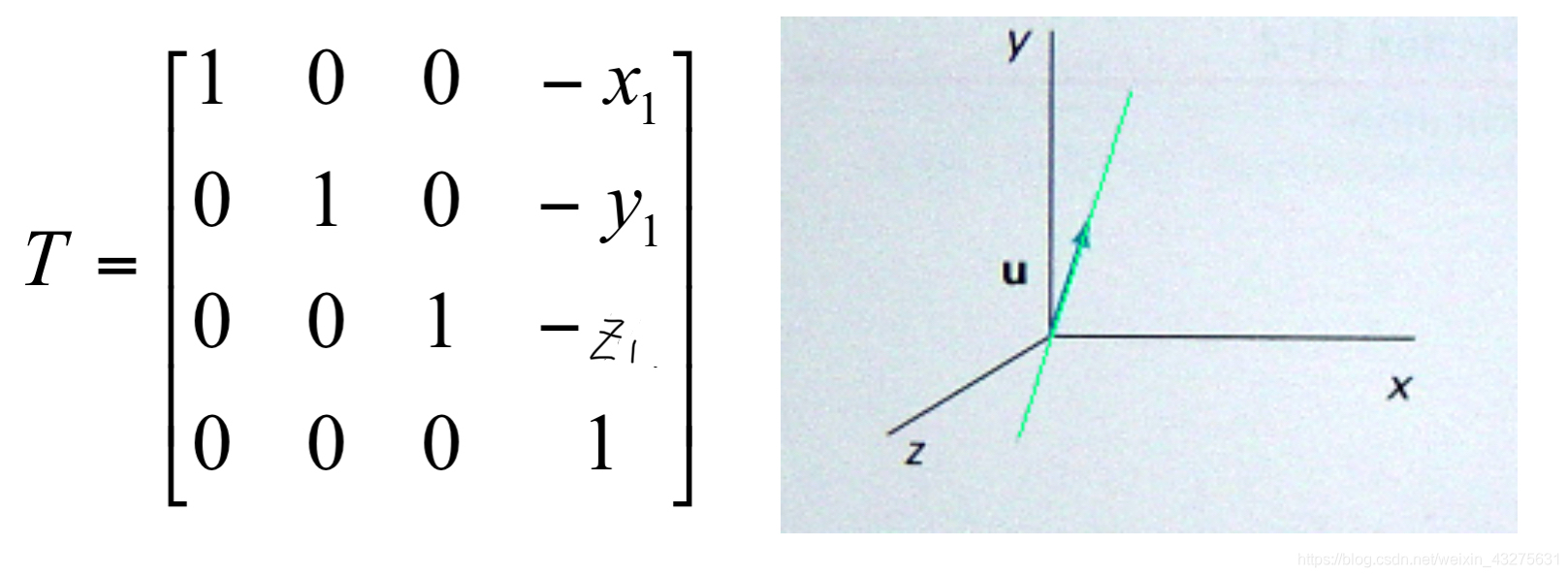
3.将u绕x轴旋转至xoz平面,效果如下图(a):
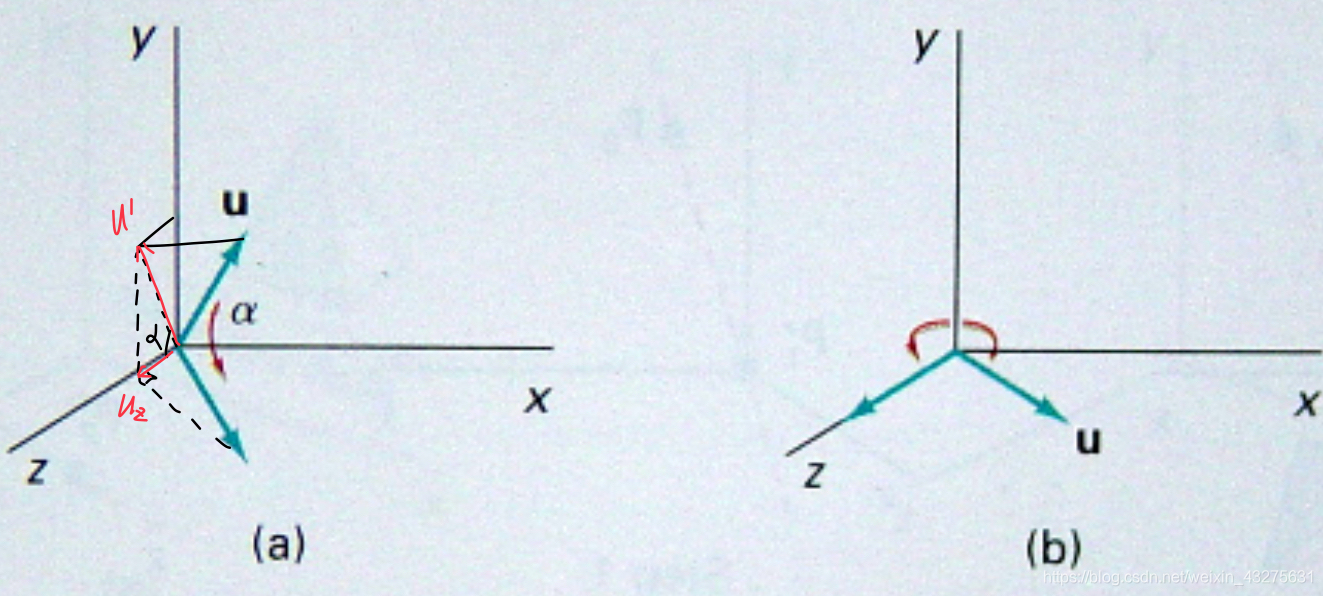
由上面的关系可以求出sinα,cosα:
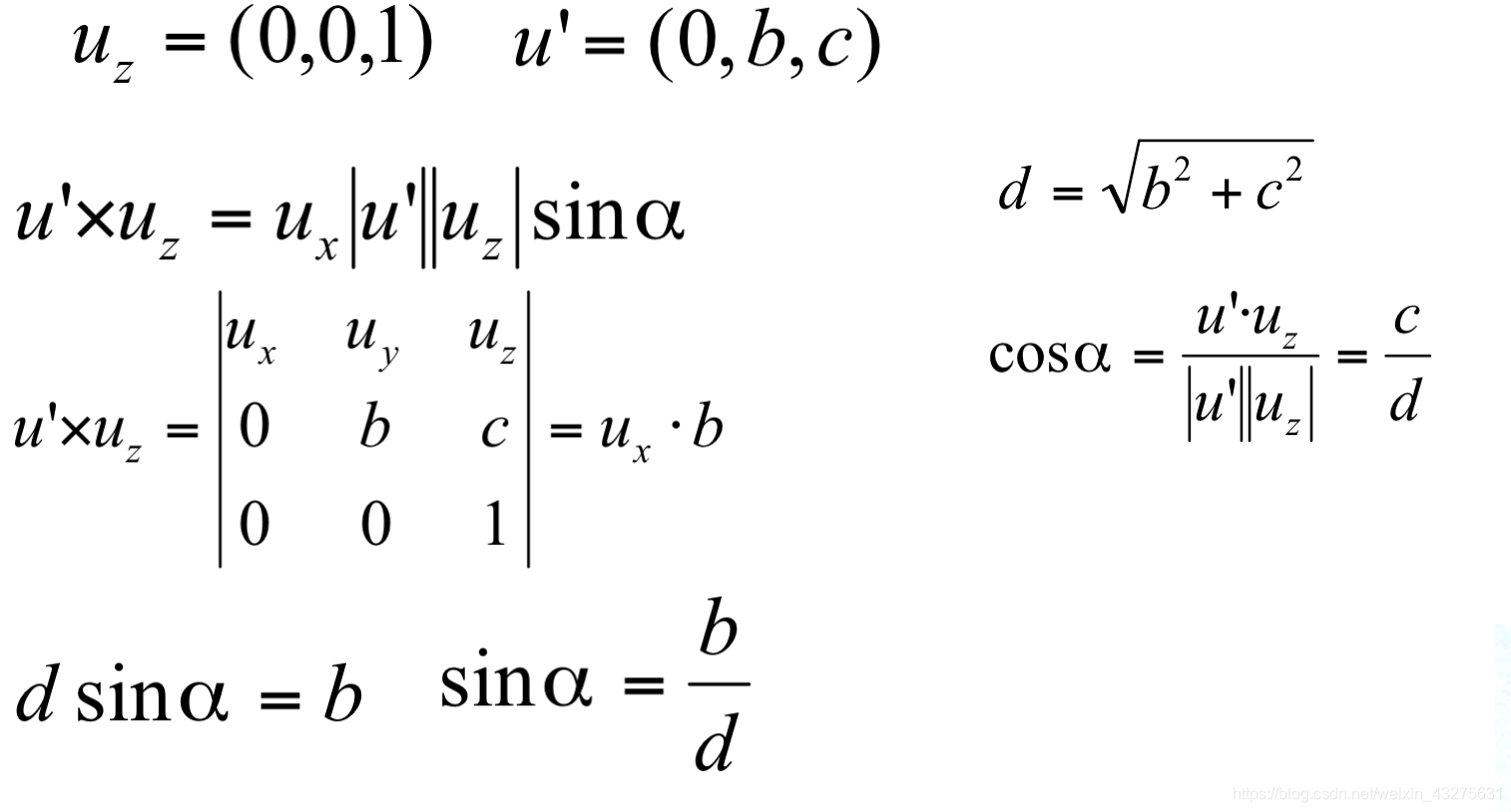
并将α带入直线绕x轴旋转矩阵Rx(θ),得到旋转矩阵Rx(α):
{
1
0
0
0
0
c
/
d
−
b
/
d
0
0
b
/
d
c
/
d
0
0
0
0
1
}
\left\{ \begin{matrix} 1& 0 & 0& 0\\ 0 & c/d & -b/d& 0\\ 0 & b/d&c/d&0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧10000c/db/d00−b/dc/d00001⎭⎪⎪⎬⎪⎪⎫
4.将xoz平面的u命名为u’’,令其绕y轴旋转β至与z轴重合:

并求出此次旋转的sinβ、cosβ、矩阵Ry(β):
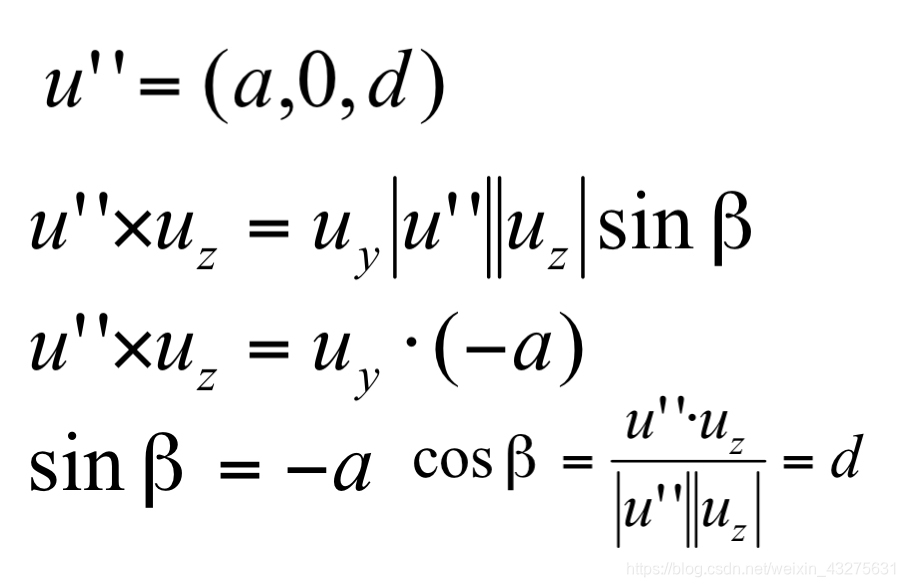
Ry(β):
{
d
0
−
a
0
0
1
0
0
a
0
d
0
0
0
0
1
}
\left\{ \begin{matrix} d& 0 & -a& 0\\ 0 & 1 & 0& 0\\ a & 0&d&0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧d0a00100−a0d00001⎭⎪⎪⎬⎪⎪⎫
最后绕z轴旋转θ,矩阵如下:
{
c
o
s
θ
−
s
i
n
θ
0
0
s
i
n
θ
c
o
s
θ
0
0
0
0
1
0
0
0
0
1
}
\left\{ \begin{matrix} cosθ& -sinθ & 0& 0\\ sinθ & cosθ & 0& 0\\ 0 & 0 & 1 &0\\ 0 & 0 & 0&1 \end{matrix} \right\}
⎩⎪⎪⎨⎪⎪⎧cosθsinθ00−sinθcosθ0000100001⎭⎪⎪⎬⎪⎪⎫
整个过程的变换矩阵为:
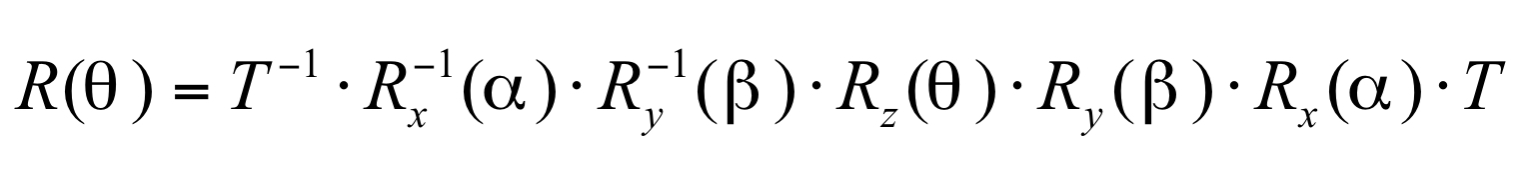

























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










