stable diffusion实践操作-采样sample

系列文章目录

stable diffusion实践操作

---

`

---

前言

采样方式和迭代步数是相辅相成的，不能分开来谈，每个采样方式都有自己的收敛迭代最佳步数。

不同的采样方法相当于我们绘画的方式不同。具体选择哪种采样方法呢？首先，我们可以参考他人使用的好看照片中所用的采样方法。如果不确定该选择哪种，我经过测试，下面圈出来的几种采样方法生成的照片质量较高且速度较快。

本文主要是B站A Eye的视频整理而来。

观看链接：Stable diffusion喂饭级基础知识教程 第四期:什么是采样方法和采样迭代步数？

---

一、采样是什么？

1.1 SD原理图

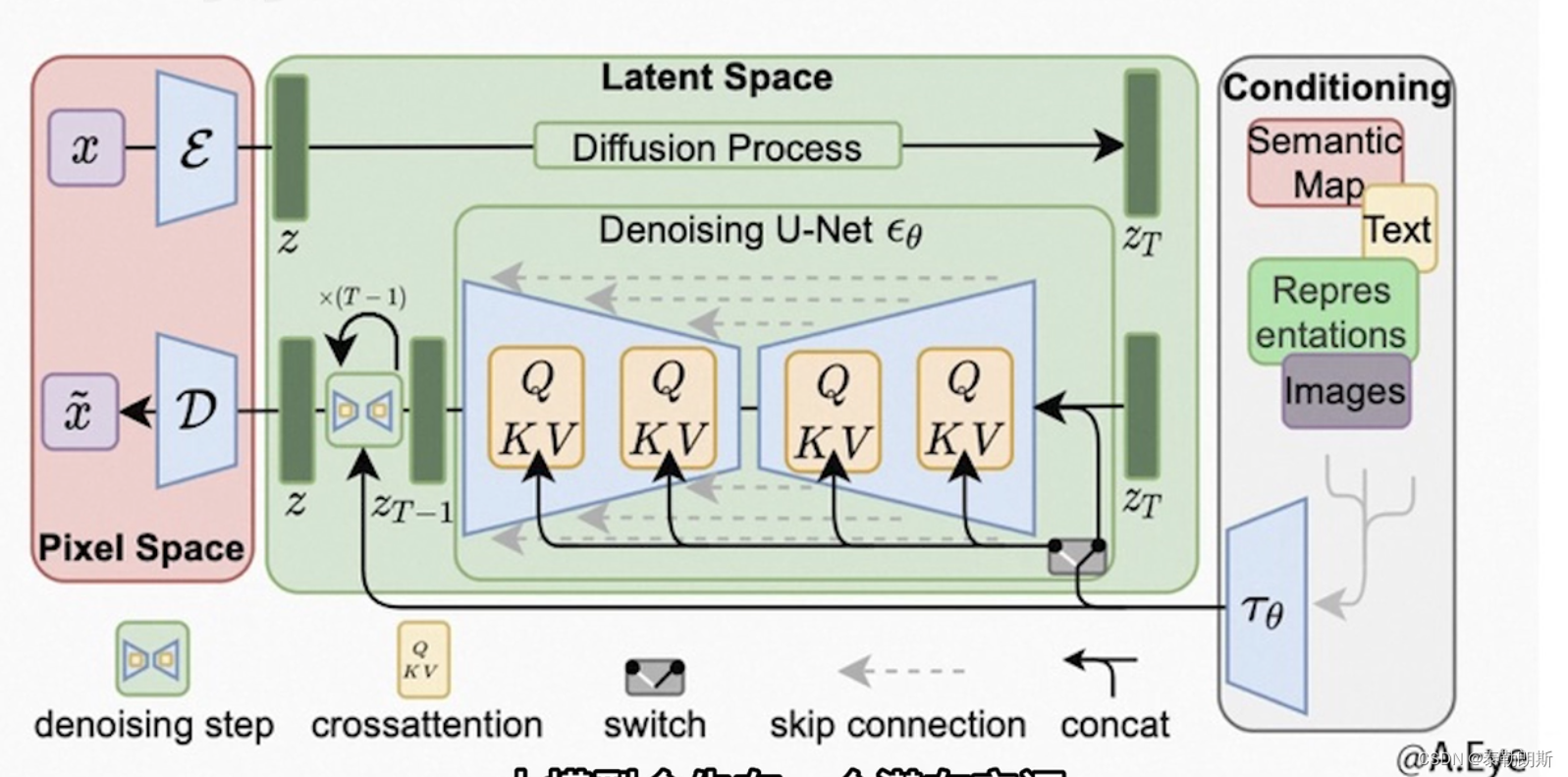
1.2 SD中采样工作流程

SD在生成图片之前，大模型会先在一个潜在的空间LatentSPaced生成一个充满噪点的图像，然后噪声预测器开始工作，从图像中减去预测到的噪声，然后不断重复这个过程。重复次数受到采样步数限制，最终得到清晰的图像。

1.3 SD重复预测采样结果

最后得到清晰的图像，简而言之SD在制作图像的过程中，都会生成一张新的去噪后的图像，整个去噪的过程即为采样，使用的采样方式就是采样器或者采样方法。

1.4 SD中采样方法列表

在webUI中，展示的采样方法

采样方法有很多，下面是采样器对比：

1.4 SD中采样方法功能总结

1.5 SD中常用采样方法

我们常用的采样方式就下面的三个，你也可以 通过XYZ图标去做对比

二、 SD中常用采样方法对比

主要从速度和收敛性来分析。
速度就看从第几步开始出图，收敛性就是看随着迭代步数增加，图片是否有不可控方向发展，如果画质细节越来越好，说明收敛性很好，否则，画质突变就说明收敛性不好。
分别对比两种风格：二次元和真人

2.1 二次元-第一组

2.1.1Euler a

从上图可以看到Euler a 从第10步就可以正常出图，后面迭代画面略有扩展，文本和模型的收敛性一般。

2.1.2Euler

从上图可以看到Euler 和Euler a差不多，但是Euler 收敛性更加强，细节更加好。

2.1.3 LMS

从上图可以看到LMS在30步以后的人收敛性才开始变得很强

2.2 二次元-第二组

2.2.1Heum

从上图可以看到Heum,从20步以上开始正常出图，和LMS采样效果很像，速度略有提升。

2.2.2 DMP2

从上图可以看到DMP2，从10步以上开始正常出图，速度不错，整体收敛性很稳定，适合做逐帧动画。

2.2.3 DMP2a

从上图可以看到DMP2a，从20步开始正常出图，但是后续迭代，细节略有扩展，类似Euler a，速度略慢Euler a.

2.3 二次元-第三组

2.3.1DPM++ 2S a

从上图可以看到DPM++ 2S a,从10步以上开始正常出图，但是在不同步数下，收敛性略差，细节变化略差。

2.3.2 DMP++ 2M

从上图可以看到DMP++ 2M，从20步以上开始正常出图，速度不错，整体收敛性很稳定，适合做逐帧动画，连续作图。

2.3.3 DMP++ SDE

从上图可以看到DMP++ SDE，从10步开始正常出图，但收敛性很差，画面完全变了，不管整体还是细节，整体太随意了。

2.4 二次元-第四组

2.4.1DPM fast

从上图可以看到DPM fast,从40步以上开始正常出图，真正的收敛性在很高步数才有。

2.4.2 DMP adaptive

从上图可以看到DMP adaptive，从10步以上开始正常出图，速度不错，整体收敛性很稳定。

2.4.3 LMS Karras

从上图可以看到LMS Karras，从10步开始正常出图，收敛性也不错。

2.5 二次元-第五组

2.5.1DPM2 Karras

从上图可以看到DPM2 Karras，从10步以上开始正常出图，表现出极好的稳定性，表现和 LMS Karras很像，但是低步数光影略胜于 LMS Karras。

2.5.2 DMP2 a Karras

从上图可以看到DMP2 a Karras，从40步以上开始正常出图，不难看出，使用了原始采样方法的人采样器，收敛性比较差。

2.5.3 DPM++ 2S Karras

从上图可以看到DPM++ 2S Karras，从10步开始正常出图，收敛性很差，后面的人图和前面的区别很大。

2.6 二次元-第六组

2.6.1DPM++ 2M Karras

从上图可以看到DPM++ 2M Karras，从10步以上开始正常出图，表现出极好的稳定性，非常完美，这也是我们推荐使用的采样器。

2.6.2 DMP++ SDE Karras

从上图可以看到DMP++ SDE Karras，从10步以上开始正常出图，收敛性比较差。

2.6.3 DDIM（元老级采样器）

从上图可以看到DDIM，从10步开始正常出图，但是整体感觉怪怪的。

2.7 二次元-第七组

2.7.1 PLMS(元老级采样器)

从上图可以看到PLMS，从40步以上开始正常出图，出图效果比较差。

2.7.2 UniPC（理论最快采样器）

从上图可以看到UniPC，从10步以上开始正常出图，低步数收敛性一般，高步数收敛性比较好。

三、迭代步数是什么

3.1 webUI上的设置位置

3.1 迭代步数定义

通过上面的分析之后，迭代步数就很好理解了，它就是从噪点到最终生成图片的步数。
步数是要通过测试才能根据模型去确定下来。

---

四、总结

采样器和迭代步数是相辅相成的。

采样器的效果会根据模型的不同表现略有差异，当选定某个模型的适合，可以使用xyz图表插件测试出图风格，最终再确定 适合自己的。

迭代步数，也要根据采样器来设置，根据不同步数，选择一个速度最高，效果最好的的步数。

所以最佳采样器和迭代步数是根据实际情况试出来的。

具体方式为xyz周，x轴为迭代步数，y轴为不同采样器。效果如下:

链接入口：xyz使用教程

以上就是今天要讲的内容。