RSA -原理介绍

学习笔记：

1、 先来看 RSA原理

RSA是1977年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）和伦纳德·阿德曼（Leonard Adleman）一起提出的。

 主要的数学原理介绍如下：

图解|什么是RSA算法_吴师兄学算法的博客-CSDN博客

欧拉函数：任意给定正整数n，请问在小于等于n的正整数之中，有多少个与n构成互质关系？

欧拉函数有个通用的计算公式：

a. 如果k是质数，则φ(k) = k-1;
b.如果 n = P * Q，P 与 Q 均为质数，则 φ(n) = φ(P * Q)= φ(P)φ(Q) = (P - 1)(Q - 1) 

欧拉定理
如果两个正整数m和n互质，那么m的φ(n)次方减去1，可以被n整除。

费马小定理
欧拉定理的特殊情况：如果两个正整数m和n互质，而且n为质数，那么φ(n)结果就是n-1

根据欧拉定理进行下面公式转换

（注：上面X等于φ(N)时候，式子5的推论成立）

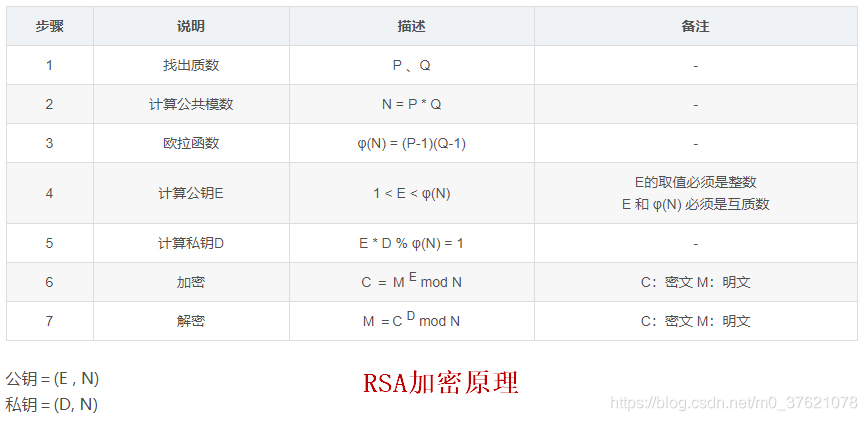
 因此，根据以上数学原理，RSA的私钥和公钥的产生过程如下：

• 1.随机选择两个质数P和Q（n=P*Q）

• 2.求N的欧拉函数值M（也就是φ(N)）

• 3.找一个与M互素的整数E

• 4.找一个整数D，满足如下关系：(E*D) mod M = 1（这里有一个术语-模逆元或模反，也就是指有一个整数d，可以使得ed被φ(N)除的余数为1。）

• 通过随机选择的互质的P和Q计算得到N、M、E、D

• 这些数字分为两组：(E,N)和(D,N)分别为公钥组和私钥组，E是公钥、D是私钥。

• 图解|什么是RSA算法_吴师兄学算法的博客-CSDN博客

• 

• RSA的加密过程满足：

  X^E mod N = Y
  其中X为明文，E为公钥，N为大整数，Y为密文，mod取余运算。（注意：数字X需要小于密钥组中的N，如果字符串转换后的数字X后大于N则需要先进行拆分）

  解密过程：

  Y^D mod N = X
  其中Y为密文，D为私钥，N为大整数，X为明文，mod取余运算。（由欧拉定理和模逆可推出）

  RSA的安全性：

  除了公钥用到n和e，其余的4个数字是不公开的（p、q、φ(n)、d）
  目前破解RSA得到的方式如下：

  要想求出私钥d，由于ed=φ(n)k+1，要知道e和φ(n)；e是知道的，但是要得到φ(n)，必须知道p、q；由于n=p*q，只有将n因式分解才能算出

  大整数的因数分解是极其困难的，属于NPC问题，所以RSA算法的安全性取决于大整数分解的难度，目前RSA算法可以支持4096位密钥长度，分解难度超乎想象，即使借助于量子计算机难度和时间都是非常非常大的。

• 

  2  OpenSSL产生key文件：

• RSA公私钥格式分析及其在Java和Openssl之间的转换方法_元子丰的博客-CSDN博客_rsa私钥格式

• 生成私钥：openssl genrsa -out prikey.pem 1024

  上面这条命令可以生成一个PKCS#1格式的，PEM格式（Base64编码+DER编码）的，1024位的RSA私钥；

  

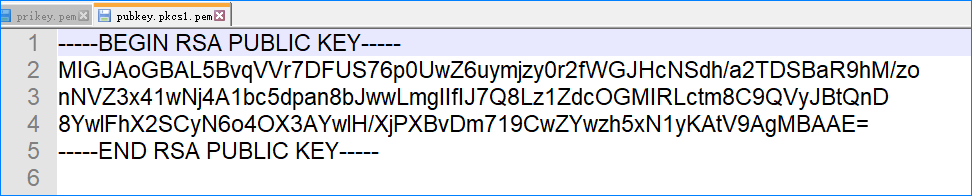
   从私钥中导出公钥：

  openssl rsa –in prikey.pem –RSAPublicKey_out –out pubkey.pkcs1.pem

  这条命令可以从RSA私钥中PKCS#1格式的、PEM编码的RSA公钥

  

  PKCS#1格式的RSA公钥

  PKCS#1格式的RSA公钥的ASN.1描述如下：

  RSAPublicKey ::= SEQUENCE { modulus INTEGER, -- n

                                                       publicExponent INTEGER -- e }

• modulus： 是RSA模数，是一个正整数
• publicExponent： 是RSA公钥幂指数，是一个正整数

• 我们用Asn1View来查看一下前面生成的pubkey.pkcs1.pem这个RSA公钥：

• 

  可以看到，它是符合PKCS标准的。其中包括了n和e这两个RSA公钥元素。其中e为65537，即0x10001，这是一个最常用的公钥幂指数。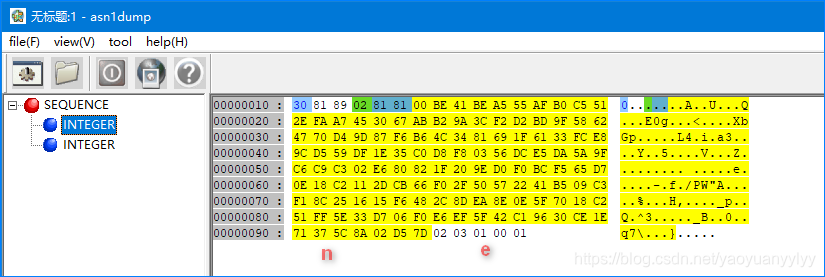
  RSA算法中的公钥指数目前在用的有两个，其一名为F0，等于3；其二名为F4，等于65537。

• PKCS#1格式的RSA私钥

  • RSAPrivateKey ::= SEQUENCE {
        version           Version, 
        modulus           INTEGER,  -- n
        publicExponent    INTEGER,  -- e
        privateExponent   INTEGER,  -- d
        prime1            INTEGER,  -- p
        prime2            INTEGER,  -- q
        exponent1         INTEGER,  -- d mod (p-1)
        exponent2         INTEGER,  -- d mod (q-1) 
        coefficient       INTEGER,  -- (inverse of q) mod p
        otherPrimeInfos   OtherPrimeInfos OPTIONAL 
    }

  • 另外还有PKCS#8格式的RSA私钥和公钥，具体信息可以查看X509文档；

•