【Simulink】光伏电池数学模型公式推导和初步仿真（FCS-MPC/扰动观察MPPT）

1. 光伏电池发电的基本原理

光伏电池发电的基本原理主要基于光电效应和半导体物理。

1️⃣ 光电效应
光伏电池的工作原理首先依赖于光电效应。光电效应是指当光子（光的粒子）照射到某些材料（如硅）上时，可以将材料中的电子激发到更高的能量状态，从而使电子脱离原子的束缚，形成自由电子-空穴对。

2️⃣ 半导体材料
光伏电池通常由半导体材料制成，最常用的材料是单晶硅、多晶硅或者薄膜材料。半导体材料在特定条件下（如掺杂）可以控制其导电性，实现光生电流的产生。

3️⃣ P-N 结的形成
光伏电池内部通过掺杂技术形成 P-N 结：

• P 型半导体：通过在硅中掺入能 提供空穴（正电荷载流子）的元素（如硼） 形成。
• N 型半导体：通过掺入能 提供自由电子（负电荷载流子）的元素（如磷） 形成。
  P-N 结的形成导致在接触面处产生电场，能够分离光生的电子和空穴。

4️⃣ 光照与电流产生
当光线（光子）照射到光伏电池表面，光子能量高于半导体材料的带隙能量时，会激发出电子，形成电子-空穴对。这些自由电子在 P-N 结形成的电场作用下，被驱动向 N 型半导体移动，而空穴则向 P 型半导体移动。

5️⃣ 电流输出
分离的电子和空穴流动形成电流。当光伏电池连接到外部负载时，电子流动产生直流电。

2. 光伏电池数学模型

光伏电池可以被等效为一个电流源和一个理想二极管的并联电路。原因如下：

1️⃣ 光伏效应产生电流
光伏电池通过光伏效应将光能转化为电能。当光照到光伏电池时，光子激发材料中的电子，形成电子-空穴对。这些电子在 P-N 结的电场作用下，从 P 型区域移动到 N 型区域，形成光生电流。因此，光伏电池的输出可以被视为一个恒定的电流源，代表了在特定光照条件下产生的光生电流。

2️⃣ 理想二极管的行为
在光伏电池中，P-N 结的存在使其具有二极管的特性。当没有光照或光照不足时，电池内会出现反向电流（通过 P-N 结的多余电子和空穴产生的），与理想二极管的反向特性相似。在正向工作时，随着电压V的增加，二极管会根据 Shockley 方程呈指数增长。

此外，考虑材料的电阻率等方面因素，在上述等效电路的基础上并联一个电阻$R_{sh}$，并串联一个电阻$R_s$。

上述模型为单二极管模型，实际上还有其他等效模型，比如双二极管、三二极管等等，参见：Słowik, Adam, et al. “An efficient approach to parameter extraction of photovoltaic cell models using a new population-based algorithm.” Applied Energy 364 (2024): 123208.

上图中，$I_L$为光生电流，$I_0$为二极管的反向饱和电流，$V_{pv}$为光伏电池输出电压，$I_{pv}$为光伏电池输出电流。

根据基尔霍夫电流定律：
$I_{p\nu }=I_L-I_D-I_{sh}$
其中，$I_D$是二极管反向电流，$I_{sh}$是并联的泄露电流（$R_{sh}$上的电流，从上到下）。

下面的公式来可以用来计算二极管反向电流$I_D$：
$I_D=I_0(e^{\frac{V_D}{V_T}}-1)=I_0(e^{\frac{q\left(V_{p\nu }+I_{p\nu }{R}_s\right)}{nkT}}-1)$
其中，$I_R$是反向电流，$I_s$是饱和电流，$V_D$是反向电压，$V_T=knT/q$是热电势。$q$为单位电荷（1.6×10^-19C），$k$为玻耳兹曼常数（1 .38×10^-23J/K），T为绝对温度（K），n为二极管指数，一般介于1～2之间。根据电路方程，$V_D=V_{p\nu }+I_{p\nu }{R}_s$。

代入原来的公式，得到：
$I_{p\nu }=I_L-I_0(e^{\frac{q\left(V_{p\nu }+I_{p\nu }{R}_s\right)}{nkT}}-1)-\frac{V_{p\nu }+I_{p\nu }{R}_s}{R_{sh}}$

3. 光伏电池简化数学模型

光伏生产商一般会提供几个重要技术参数，包括 $I_{sc}$（短路电流 Short-circuit current）、$V_{oc}$（开路电压 Open circuit voltage）、$I_m$（最大功率点的负载电流）、$V_m$（最大功率点的负载电压）、$P_m$ （最大功率 Maximum Power）、T（光伏温度）和 S（光照强度）。接下来基于上述参数构建模型。

在之前求出的数学模型的基础上作简化，得到工程模型：

1）等效串联电阻$R_s$远远小于等效并联电阻$R_{sh}$，所以光生电流$I_L$远远大于光伏电池的漏电流$I_{sh}$，忽略上式的最后一项，即：
$I_{p\nu }=I_L-I_0(e^{\frac{q\left(V_{p\nu }+I_{p\nu }{R}_s\right)}{nkT}}-1)$

2）等效串联电阻$R_s$远远小于PN结正向导通电阻，当光伏电池发生短路时，其短路电流$I_{sc}$可等效为光生电流$I_L$，即：
$I_{p\nu }=I_{sc}-I_0(e^{\frac{q\left(V_{p\nu }+I_{p\nu }{R}_s\right)}{nkT}}-1)$

3）在标准状况条件下，将光伏电池的开路电压等于标准环境条件下的开路电压$V_{oc}$，光伏电池的峰值电压等于标准环境条件下的峰值电压$V_m$，光伏电池的峰值电流等于标准环境条件下的峰值电流$I_m$。

设参数 $C_1$ 和 $C_2$：
$C_1=\left(1-\frac{I_m}{I_{sc}}\right)e^{\left(-\frac{V_m}{C_2{V}_{oc}}\right)}$
$C_2=\left(\frac{V_m}{V_{oc}}-1\right){\left[\ln \left(1-\frac{I_m}{I_{sc}}\right)\right]}^{-1}$

代入光伏电池输出电流公式，得到：
$I_{pv}=I_{sc}\left(1-C_1\left(e^{\frac{V_{pv}}{C_2{V}_{oc}}}-1\right)\right)$

在标准状况条件下，可通过光伏电池的峰值电压、峰值电流、开路电压、短路电流求得参数 $C_1$ 和 $C_2$，得到光伏电池在标准环境条件下的输出特性。

一般峰值电压、峰值电流、开路电压、短路电流这些参数会受到太阳的光照强度 S 和温度 T 影响。当日射强度及电池温度不是参考日射强度和参考电池温度时，必须考虑环境温度条件对太阳电池特性的影响。对这些参数在实际温度和光照强度条件（标准电池温度 $T_{ref}$ (比如25℃) ）和标准光照强度 $S_{ref}$ (比如1000W/m^2)）下进行折算：
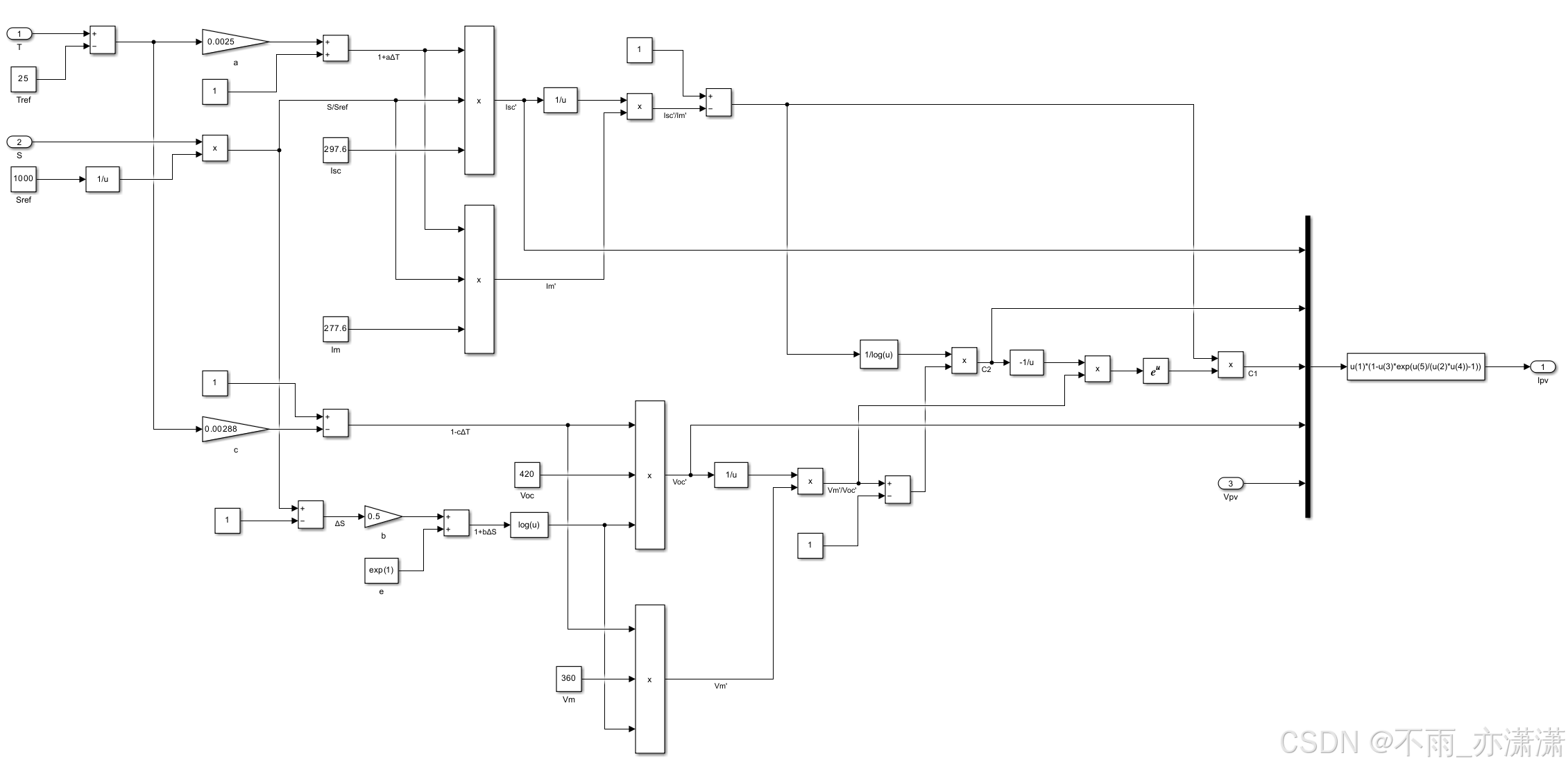
$\begin{array}{l}\Delta T=T-T_{ref}\\ \Delta S=\frac{S}{S_{ref}}-1\\ I_{sc}^{\prime }=I_{sc}\frac{S}{S_{ref}}(1+\alpha \Delta T)\\ V_{oc}^{\prime }=V_{oc}(1-c\Delta T)\ln (1+b\Delta S)\\ I_m^{\prime }=I_m\frac{S}{S_{ref}}(1+\alpha \Delta T)\\ V_m^{\prime }=V_m(1-c\Delta T)\ln (1+b\Delta S)\end{array}$
推算过程中假定 I-V 特性曲线基本形状不变，系数a、b、c的典型值为：a=0.0025/℃，b=0.5，c=0.00288/℃。

除此之外，还有另一种处理方式，详见：[1] 杨鲁发.光伏并网发电系统MPPT和孤岛检测技术的研究和实现[D].华北电力大学（河北）,2010. 和 [5] 苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,(04):409-412. 中的方法1。

4. Simulink模型构建

Simulink自带的 PV Array 模块：

内部：

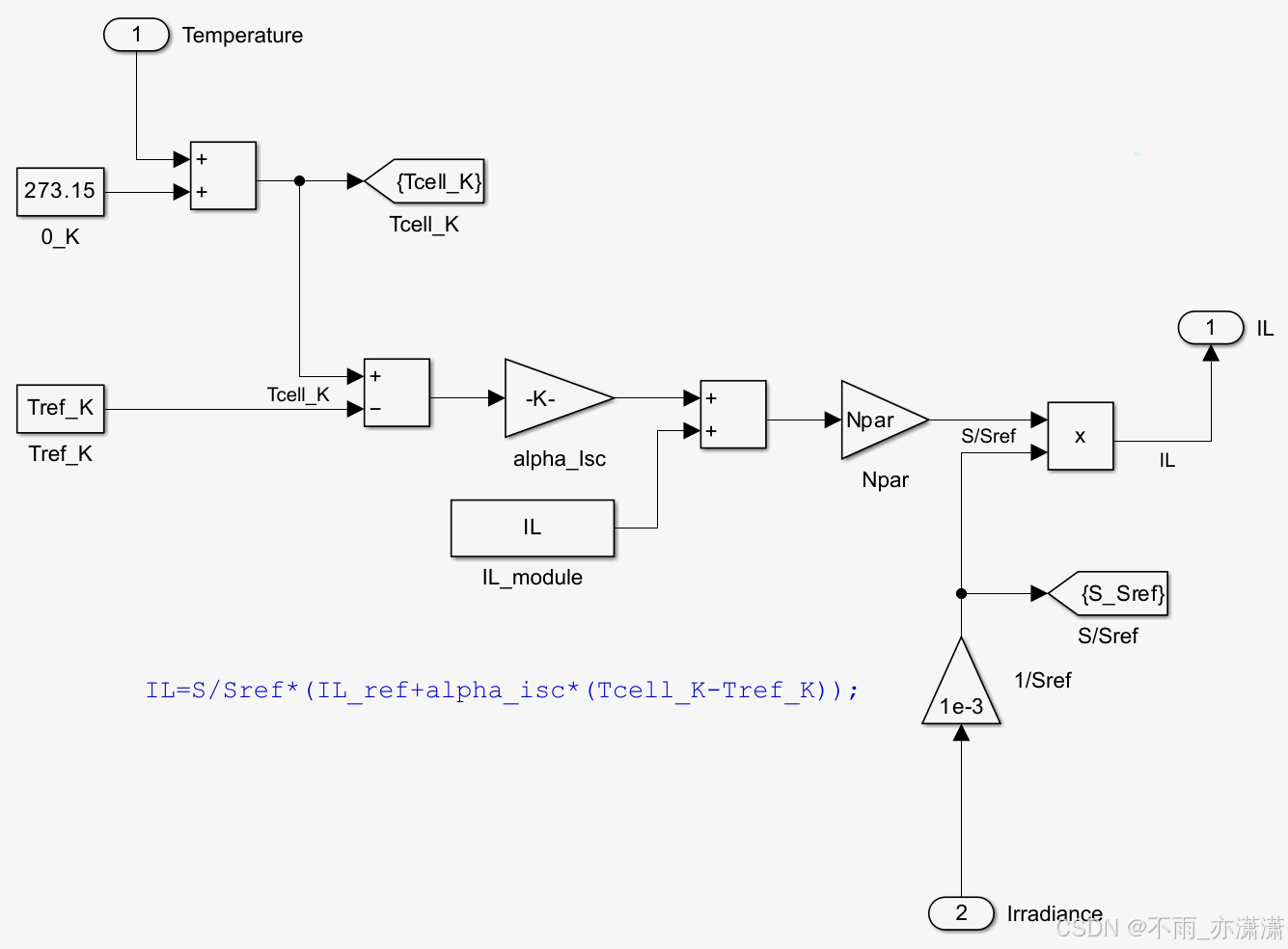
我们可以参考模块内部，建立光伏电池仿真模型。

外接boost变换器和阻性负载，控制部分采用PI+FCS-MPC试试。

负载端电压：

稳定在540V左右。

为了充分利用光伏电池的输出量，最大程度的发挥光伏电池的作用，实际上一般采用MPPT算法使光伏电池工作在最大功率点。

MPPT-扰动观察

MPPT：

光伏输出功率：

最大功率的计算即为Vm*Im (单个电池)

再比如：

最大功率 Pm = 29 * 7.35 * 10 * 40 = 85260

绘制 I-V、P-V 曲线

T=25℃，S=1000W/m^2

I-V

P-V

T=25℃，S=800W/m^2

I-V

P-V

T=20℃，S=1000W/m^2

I-V

P-V

很明显，不同温度、光照强度下的光伏特性I-V、P-V曲线不同。

模型：https://mbd.pub/o/bread/Zp6ZlJts

参考

[1] 杨鲁发.光伏并网发电系统MPPT和孤岛检测技术的研究和实现[D].华北电力大学（河北）,2010.

[2] 关皓闻.含光伏发电系统的负荷模型参数辨识及电网稳定性研究[D].华北电力大学,2022.

[3] Słowik, Adam, et al. “An efficient approach to parameter extraction of photovoltaic cell models using a new population-based algorithm.” Applied Energy 364 (2024): 123208.

[4] 童俊杰,叶成彬,陈贤钰,等.基于太阳能的电动车光蓄能源供电管理系统[J].环境技术,2021,39(03):111-116+130.

[5] 苏建徽,余世杰,赵为,等.硅太阳电池工程用数学模型[J].太阳能学报,2001,(04):409-412.

基于MATLAB/Simulink的光伏电池物理、工程模型建模仿真