本文基于光学原理和波动理论,用Matlab实现迈克尔逊等倾干涉现象仿真。
迈克尔逊干涉原理
- 实验装置:

- 光强分布公式:
产生光程差大小 Δ = 2 n d c o s i \Delta=2nd cosi Δ=2ndcosi;( i i i为光源S在M1上的入射角,n为折射率)
由光波叠加原理,干涉光强分布公式: I = 2 I 0 c o s 2 ( π Δ λ ) I=2I_0cos^2(\frac {\pi\Delta} {\lambda}) I=2I0cos2(λπΔ)
其中,在屏幕前加上焦距为f的透镜,则 i i i可表示为: i = a r c t a n x 2 + y 2 f i=arctan\frac {\sqrt{x^2+y^2}} {f} i=arctanfx2+y2
Project Code
% 作者:ZQJ
% 日期:2021.1.28 星期四
%***********************模拟迈克尔逊等倾干涉图样**************************
clear,clc,close all;
% 基本参数输入及处理*********************************
% 本例输入:Lambda = 632.8; d = 0.2;
Lambda = input('输入光的波长(单位为nm):');
Lambda = Lambda * 1e-9; %波长单位转为:m
d = input('输入M1和M2’之间的距离(单位为mm):');
d = d * 1e-3; %距离d单位转为:m
f = 0.1; %透镜的焦距:m
I0 = 1; %入射光的光强
Screen_length = 0.015; %定义干涉仿真范围:m
[Screen_x,Screen_y] = meshgrid(linspace(-Screen_length,Screen_length,800));
interference_r = abs(Screen_x + 1i*Screen_y);
I_delta = (2*pi*d/Lambda).*cos(atan(interference_r./f));
I = 2*I0*(cos(I_delta)).^2;
I = I./max(max(I)); %光强分布归一化
% 迈克尔逊等倾干涉光强分布图*************************
I = I*64; %光强归一,扩大显示
image(Screen_x(1,:),Screen_y(:,1),I); %设置x和y的像素,显示数值
colormap hot; %妆点色彩
colorbar;
xlabel('空间坐标x'),ylabel('空间坐标y');
title('迈克尔逊等倾干涉光强空间分布');
仿真结果图:
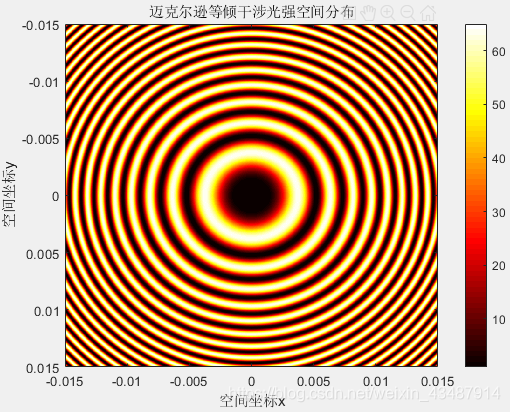
专栏内容供作者本人或大家学习使用,多多指教 ~








 本文介绍了基于光学原理和波动理论,利用Matlab进行迈克尔逊等倾干涉现象的仿真。通过输入光的波长和两反射镜间距离,计算光强分布,并展示干涉光强的空间分布图。代码实现详细,适合学习光学和仿真技术的读者参考。
本文介绍了基于光学原理和波动理论,利用Matlab进行迈克尔逊等倾干涉现象的仿真。通过输入光的波长和两反射镜间距离,计算光强分布,并展示干涉光强的空间分布图。代码实现详细,适合学习光学和仿真技术的读者参考。
















 988
988

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








