4.8 案例:21点游戏
一、游戏规则
本节考虑纸牌游戏“21点”(Blackjack-v0),为其实现游戏AI。
21点的游戏规则是这样的:游戏里有一个玩家(player)和一个固定策略的庄家(dealer),牌的数量是无限(有替换)的,每次取牌的概率是固定的。游戏开始时玩家和庄家都有两张牌,庄家的一张牌是亮出来的。接着,玩家可以选择是不是要更多的牌,每个回合的结果可能是玩家获胜、庄家获胜或打成平手。
简化版的玩家动作:只有两种:一种是拿牌,另一种是停牌。
- 拿牌(HIT):如果玩家拿牌,表示玩家希望再拿一张或多张牌,使总点数更接近21点。如果拿牌后玩家的总点数超过21点,玩家就会Bust。
- 停牌(STAND):如果玩家停牌,表示玩家选择不再抽牌并希望当前总点数能够打败庄家
状态:是玩家的点数(Player),庄家的点数(Dealer)和是否有Blackjack(Ace)。具体到代码中,player为玩家点数,dealer为庄家点数,ace为True时表明牌A算作11点
确定A牌的点数:首先要保证玩家手上牌的总点数小于21(所以至多有一张A牌会算作11),在此基础上让总点数尽量大。在计算庄家点数时,总是将A计算为1点(当然总是计算为11点也是完全等价的)
结果:如果点数和大于21,则称玩家输掉这一回合,庄家获胜;如果点数和小等于21,那么玩家可以再次决定是否要更多的牌,直到玩家不再要更多的牌。如果玩家在总点数小等于21的情况下不要更多的牌,那么这时候玩家手上的总点数就是最终玩家的点数。
接下来,庄家展示其没有显示的那张牌,并且在其点数小于17的情况下抽取更多的牌。如果庄家在抽取的过程中总点数超过21,则庄家输掉这一回合,玩家获胜;如果最终庄家的总点数小于等于21,则比较玩家的总点数和庄家的总点数。如果玩家的总点数大于庄家的总点数,则玩家获胜;如果玩家和庄家的总点数相同,则为平局;如果玩家的总点数小于庄家的总点数,则庄家获胜。
各牌面对应的点数见表4-1,其中牌面A代表1点或11点。
| 牌面 | 点数 |
|---|---|
| A | 1或11 |
| 2 | 2 |
| 3 | 3 |
| … | … |
| 9 | 9 |
| 10, J ,Q, K | 10 |
二、代码详解
4.8.1 实验环境的使用
import gym
#这里需要下载文本网址https://www.lfd.uci.edu/~gohlke/pythonlibs/#pygame
# 导入pyplot并将其命名为plt
import matplotlib.pyplot as plt
import numpy as np
env = gym.make('Blackjack-v1')
env = env.unwrapped # 据说不做这个动作会有很多限制,unwrapped是打开限制的意思
env.reset()#初始化环境
env.step(action)
1.env.step()函数的参数是动作,它可以是int型数值0或1,其中0表示玩家不再要更多的牌,1表示玩家再要一张牌。env.step()的第0个返回值是观测,它是一个有3个元素的tuple值,其3个元素依次为:
范围为3~21的int型数值,表示玩家的点数和;
范围为1~10的int型数值,表示庄家可见牌的点数;
bool型数值,表示在计算玩家点数和的时候,是否有将1张A牌计算为11点。
代码4-1、用随机策略玩一个回合
#游戏网站https://www.casinotop10.net/blackjack
print(env.action_space)
#env.action_space查看这个环境中可用的action有多少个,返回Discrete()格式
print(env.observation_space)#env.observation_space查看这个环境中可用的observation有多少个,返回Discrete()格式
#-------------------用随机策略玩一个回合--------------------
observation=env.reset()
print('观测={}'.format(observation))
while True:
print('玩家 = {},庄家 = {}'.format(env.player,env.dealer))
#查看这个环境中可用的action有多少个,返回int
action=np.random.choice(env.action_space.n)
print('动作 = {}'.format(action))
#获取下一步的环境、得分、检测是否完成。
observation,reward,done,_=env.step(action)
print('观测 = {},奖励 = {},结束指示 = {}'.format(observation,reward,done))
if done:
break#回合结束
Numpy库的np.random.choice()函数选择动作。numpy.random.choice(a, size=None, replace=True, p=None)
这个函数的第0个参数表示要从哪些数据里选择。它还可能有一个关键字参数p,表示选择各数据的概率,代码没有指定关键字参数p,则表示等概率选择数据。
运行结果
Discrete(2)
Tuple(Discrete(32), Discrete(11), Discrete(2))#状态空间
#Discrete(32)的范围是0-31,游戏中没有0的牌,1-31表示玩家的牌的和,注意如果玩家到了21点肯定不会再要牌,因此即使爆了最大和也最多是20+11=31;
观测=(15, 7, False)
玩家 = [6, 9],庄家 = [7, 10]
动作 = 0
观测 = (15, 7, False),奖励 = -1.0,结束指示 = True
- 2代表有2个离散action,是一个类,并且继承一个space类,0或1 要牌或放弃
- 第一个tuple中分别代表,当前玩家手中的牌总和,对方展示牌大小,以及我方是否有usable Ace后面是奖励,以及当前幕是否结束。
- 总状态数有下面三个维度:自己手中的点数和(12到21)。庄家明牌的点数(A到10);庄家明牌是否有 A(True, False)。
代码4-3 同策回合更新策略评估
21点游戏的交互可以看作一个Markov决策过程。我们将观测略做修改,将观测tuple的最后一个元素改为int值,就可以得到用3个int值表示的状态,见以下代码
在21点游戏中的轨迹特点:
- 不可能出现重复的状态——牌的总点数增加。
- 最后的奖励值就是回合的总奖励值——在一个轨迹中只有最后的一个奖励值是非零值,$ \gamma=1$。
- 不需要区分首次访问和每次访问——都是首次访问;
- 同策更新不需要逆序求回报——一个游戏内的所有奖励都是零,在折扣因子 γ = 1 \gamma=1 γ=1的情况下,只要将回合最后一个奖励值作为回报值,
算法4-3 给出了on-policy回合更新策略评估的算法。函数evaluate_action_monte_carlo()根据环境env和策略policy,求得动作价值函数q并返回。在这个函数中,不区分首次访问和每次访问,限定 γ = 1 \gamma= 1 γ=1 并直接用最后的奖励值作为回报值 g g g,而且在更新状态时是顺序更新的。
#----------------------回合更新预测-----------------------------
#从观测到状态
def ob2state(observation):
return(observation[0],observation[1],int(observation[2]))
#同策回合更新策略评估
def evaluate_action_monte_carlo(env, policy, episode_num=500000):
#例如模型训练中途或迭代结束后,玩一轮游戏(例如玩一局飞机大战)看看本局游戏能得多少奖励。无论通关还是失败,都是一个episode。
q = np.zeros_like(policy)
c = np.zeros_like(policy)
# 按照设定的episode_num数量进行对应迭代
# 按照输入的策略,采集episode
for _ in range(episode_num):#’_’ 是一个循环标志,也可以用i,j 等其他字母代替
# 玩一回合
state_actions = []
observation = env.reset()
while True:
state = ob2state(observation)
# 获取当前状态是预定策略将会采取的动作
action = np.random.choice(env.action_space.n, p=policy[state])
state_actions.append((state, action))
# 与环境交互,获取下一个状态,奖励,以及结束标志位
observation, reward, done, _ = env.step(action)
if done:
break # 回合结束
g = reward # 回报
for state, action in state_actions:
c[state][action] += 1.
q[state][action] += (g - q[state][action]) / c[state][action] #p58 2.2.5
return q
- step 方法的输入为玩家的决策动作(叫牌还是结束),并输出observation, reward, done, _ 。简单解释一下代码逻辑,当玩家继续加牌时,需要判断是否超21点,如果没有超过的话,返回下一状态,同时reward 为0,等待下一step方法。若玩家停止叫牌,则按照庄家策略:小于17时叫牌。游戏终局时产生+1表示玩家获胜,-1表示庄家获胜。数据集的类型为List[Tuple[State, Action, Reward]]
range(start, stop[, step]),分别是起始、终止和步长
evaluate_action_monte_carlo()函数的用法:
#evaluate_action_monte_carlo()函数的用法
policy = np.zeros((22, 11, 2, 2))
policy[20:, :, :, 0] = 1 # >= 20 时收手
policy[:20, :, :, 1] = 1 # < 20 时继续
q = evaluate_action_monte_carlo(env, policy) # 动作价值
v = (q * policy).sum(axis=-1) # 状态价值
$ v_{\pi}(s)=\sum_{a}\pi(a|s)q_{\pi}(s,a)$
policy被初始化为一个4维数组,第一维表示玩家手牌的点数1-21(0和1实际没有用到),第二维表示庄家手牌点数,第三维表示玩家手牌是否有A计算为11点,第四维是玩家要采取的动作(0-停牌,1-要牌)
代码4-4 绘制最后一维的指标为0或1的3维数组
# 绘制最后一维的指标为0或1的3维数组
#绘制最后一维的指标为0或1的3维数组
def plot(data):
#它是用来创建 总画布/figure“窗口”的
fig, axes = plt.subplots(1, 2, figsize=(9, 4))
titles = ['without ace', 'with ace']
have_aces = [0, 1]
extent = [12, 22, 1, 11]
for title, have_ace, axis in zip(titles, have_aces, axes):
dat = data[extent[0]:extent[1], extent[2]:extent[3], have_ace].T
axis.imshow(dat, extent=extent, origin='lower')
axis.set_xlabel('player sum')
axis.set_ylabel('dealer showing')
axis.set_title(title)
plt.show()
plot(v)
运行结果

代码4-5 带起始探索的同策回合更新
在函数内部,每个游戏回合前都随机产生一个状态动作对。利用产生的状态,可以反推出一种玩家的持牌可能性和庄家持有的明牌。考虑所有对应到相同状态的玩家持牌都是等价的,所以这里只需任意指定一种玩家的持牌即可。计算得到玩家的持牌和庄家持有的明牌后,可以直接将牌面赋值给env.player和env.dealer[0],告知环境当前状态。这样,该回合游戏就可以从给定的起始状态开始了。
# ----------带起始探索的同策回合更新---------------------------
def monte_carlo_with_exploring_start(env, episode_num=500000):
policy = np.zeros((22, 11, 2, 2))
policy[:, :, :, 1] = 1.
q = np.zeros_like(policy)
c = np.zeros_like(policy)
for _ in range(episode_num):
# 随机选择起始状态和起始动作
state = (np.random.randint(12, 22),
np.random.randint(1, 11),
np.random.randint(2))
action = np.random.randint(2)
# 玩一回合
env.reset()
if state[2]: # 有A
env.player = [1, state[0] - 11]
else: # 没有A
if state[0] == 21:
env.player = [10, 9, 2]
else:
env.player = [10, state[0] - 10]
env.dealer[0] = state[1]
state_actions = []
while True:
state_actions.append((state, action))
observation, reward, done, _ = env.step(action)
if done:
break # 回合结束
state = ob2state(observation)
action = np.random.choice(env.action_space.n, p=policy[state])
g = reward # 回报
for state, action in state_actions:
c[state][action] += 1.
q[state][action] += (g - q[state][action]) / c[state][action]
a = q[state].argmax()
policy[state] = 0.
policy[state][a] = 1.
return policy, q
policy, q = monte_carlo_with_exploring_start(env)
v = q.max(axis=-1)
plot(policy.argmax(-1))
plot(v)
运行结果
观测=(13, 3, True)
玩家 = [1, 2],庄家 = [3, 6]
动作 = 1
观测 = (13, 3, False),奖励 = 0.0,结束指示 = False
玩家 = [1, 2, 10],庄家 = [3, 6]
动作 = 1
观测 = (22, 3, False),奖励 = -1.0,结束指示 = True

图4-3 最优策略图像(黄色表示继续要牌,紫色表示不要牌)
分析:左图:庄家的某张明牌就是你停止要牌的最小点数。例如,庄家的明牌是7,停止要牌的点数是17.这是你硬点数牌型时要达到的目标。你在拿到硬17点或更高时就停止要牌。在你拿到硬16点或更少时,继续要牌。如果庄家的明牌是6,停止要牌的点数降到13!你在13点或以上就停止要牌,11点或更少时才要牌。
右图:玩家拿到硬11点或以下时应该无条件要牌。相似地,如果玩家的牌是软16点或以下也不会有什么损失。再拿一张牌无论如何不会爆掉,因为总和超过21点以后,A会被自动计为1点。如果又要到一张A,它会被计为1点,任何其他的牌可能会是一个数字10或更少。因为玩家持有软17点或更小不会爆掉,他不会让这个组合变得更差。因为最终,总共17点或低于17点是等同的。如果你停止要牌而庄家爆掉,你一样会赢。如果你是17点或更低,而庄家没有爆掉,那庄家按照规则来说一定是17到21点中间的某个点数,玩家一样是输。所以,在软17点或更低时,继续要牌是没有坏处的。
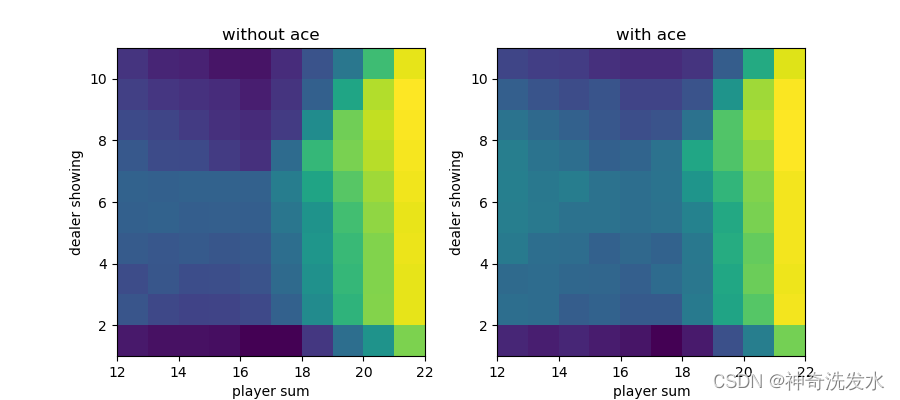
图4-4 最优策略状态价值函数图像
最优值函数
v
∗
(
s
)
v _∗ ( s )
v∗(s))是在从所有策略产生的状态值函数中,选取使状态s价值最大的函数,即:
v
∗
(
s
)
=
max
π
v
π
(
s
)
v _∗ ( s ) ={\max\limits_{\pi}} v_\pi(s)
v∗(s)=πmaxvπ(s)
最优状态行为值函数$ q^*(s,a)$ 在所有策略中最大的状态-行为值函数,即
q
∗
(
s
,
a
)
=
max
π
q
π
(
s
,
a
)
q^*(s,a)=\max\limits_\pi q_\pi(s,a)
q∗(s,a)=πmaxqπ(s,a)
代码4-6 基于柔性策略的同策回合更新
上面实现的是确定性的策略,执行动作的概率不是0就是1,接下来介绍一种不确定性的策略一$ε-soft $policy,即在一个状态s下每个动作的概率都是 ε / n ε/n ε/n给最优的动作的概率加上 1 − 1- 1−ε,将策略初始化为 π ( a ∣ s ) = 0.5 \pi(a|s)=0.5 π(a∣s)=0.5,这样可以确保初始化的策略也是ε柔性策略,ie可以选择所有可能的动作,所以从一个状态出发可以达到这个状态能达到的所有状态和所有状态动作对,
#--------------基于柔性策略的同策回合更新--------------
# 柔性策略重要性采样最优策略求解
def monte_carlo_with_soft(env, episode_num=500000, epsilon=0.1):
policy = np.ones((22, 11, 2, 2)) * 0.5 # 柔性策略
q = np.zeros_like(policy)
c = np.zeros_like(policy)
for _ in range(episode_num):
# 玩一回合
state_actions = []
observation = env.reset()
while True:
state = ob2state(observation)
action = np.random.choice(env.action_space.n, p=policy[state])
state_actions.append((state, action))
observation, reward, done, _ = env.step(action)
if done:
break # 回合结束
g = reward # 回报
for state, action in state_actions:
c[state][action] += 1.
q[state][action] += (g - q[state][action]) / c[state][action]
# 更新策略为柔性策略
a = q[state].argmax()
policy[state] = epsilon / 2.
policy[state][a] += (1. - epsilon)
return policy, q
policy, q = monte_carlo_with_soft(env)
v = q.max(axis=-1)
plot(policy.argmax(-1))
plot(v)
运行结果

图4-3 最优策略图

图4-4 最优策略状态价值函数图像
代码4-7 异策策略评估
接下来考虑off-policy算法。以下代码给出了基于重要性采样的策略评估求解动作价值函数。函数evaluate_monte_carlo_importance_resample不仅有表示目标策略的参数policy,还有表示行为策略的参数behavior_policy。在回合更新的过程中,为了有效地更新重要性采样比率,所以需要采用逆序更新。
#----------------------------重要性采样策略评估-------------------
def evaluate_monte_carlo_importance_resample(env, policy, behavior_policy, episode_num=500000):
q = np.zeros_like(policy)
c = np.zeros_like(policy)
for _ in range(episode_num):
# 用行为策略玩一回合
state_actions = []
observation = env.reset()
while True:
state = ob2state(observation)
action = np.random.choice(env. action_space.n, p=behavior_policy[state])
state_actions.append((state, action))
observation, reward, done, _ = env.step(action)
if done:
break # 玩好了
g = reward # 回报
rho = 1. # 重要性采样比率
for state, action in reversed(state_actions):
c[state][action] += rho
q[state][action] += (rho / c[state][action]*(g - q[state][action]))#p64 2.4.2
rho *= (policy[state][action]/ behavior_policy[state][action]) #p65 2.4.3
if rho == 0:
break # 提前终止
return q
policy = np.zeros((22, 11, 2, 2))
policy[20:, :, :, 0] = 1 # >= 20时收手
policy[:20, :, :, 1] = 1 # <20时继续
behavior_policy = np.ones_like(policy) * 0.5 #初始化的策略是柔性策略
q = evaluate_monte_carlo_importance_resample(env, policy, behavior_policy)
v = (q * policy).sum(axis=-1)
plot(v);
运行结果
函数的用法如下列代码所示。其中的行为策略是$ π(a∣s)=0.5( s∈\mathcal{S},a∈\mathcal{A})$该代码可以生成与on-policy回合更新一致的结果。
观测=(11, 7, False)
玩家 = [8, 3],庄家 = [7, 10]
动作 = 1
观测 = (17, 7, False),奖励 = 0.0,结束指示 = False
玩家 = [8, 3, 6],庄家 = [7, 10]
动作 = 1
观测 = (26, 7, False),奖励 = -1.0,结束指示 = True

代码4-8 柔性策略重要性采样最有策略求解
最后来看off-policy回合更新的最优策略求解。代码清单4-8给出了基于重要性采样的最优策略求解。在函数的初始化阶段确定了行为策略为$\π ( a ∣ s ) = 0.5 ( s ∈ S , a ∈ A $这是一个柔性策略。在后续的回合更新中,无论目标策略如何更新,都使用这个策略作为行为策略。在更新阶段,同样使用逆序来有效更新重要性采样比率
# 柔性策略重要性采样最优策略求解
def monte_carlo_importance_resample(env, episode_num=500000):
policy = np.zeros((22, 11, 2, 2))
policy[:, :, :, 0] = 1.
behavior_policy = np.ones_like(policy) * 0.5 # 柔性策略
q = np.zeros_like(policy)
c = np.zeros_like(policy)
for _ in range(episode_num):
# 用行为策略玩一回合
state_actions = []
observation = env.reset()
while True:
state = ob2state(observation)
action = np.random.choice(env.action_space.n, p=behavior_policy[state])
state_actions.append((state, action))
observation, reward, done, _= env.step(action)
if done:
break # 玩好了
g = reward # 回报
rho = 1. # 重要性采样比率
for state, action in reversed(state_actions):
c[state][action] += rho
q[state][action] += (rho / c[state][action]*(g - q[state][action])) #p65 2.4.2
# 策略改进
a = q[state].argmax()
policy[state] = 0.
policy[state][a] = 1.
if a != action: # 提前终止
break
rho /= behavior_policy[state][action]
return policy, q
policy, q = monte_carlo_importance_resample(env)
v = q.max(axis=-1)
plot(policy.argmax(-1))
plot(v)
运行结果
与同策回合更新结果一致

最优策略图像
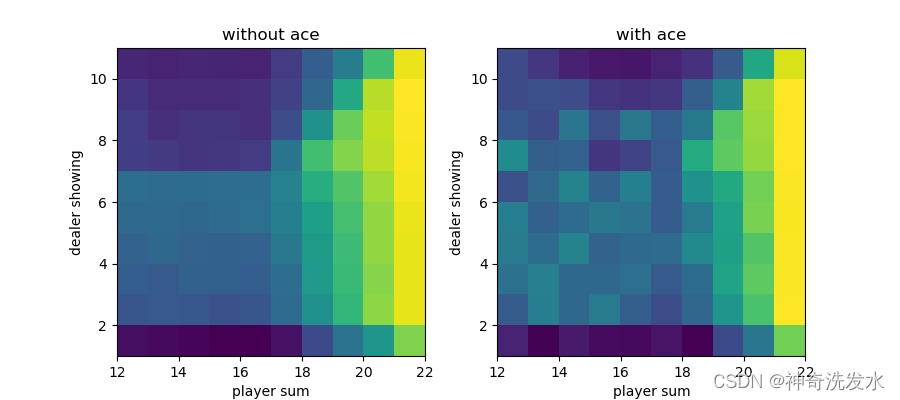
最优策略状态价值函数图像
























 4452
4452

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








