逻辑回归（LR）原理讲解

本质：本质为线性回归，在特征到结果的映射当中加了逻辑函数g(z)
其中：

则：

其中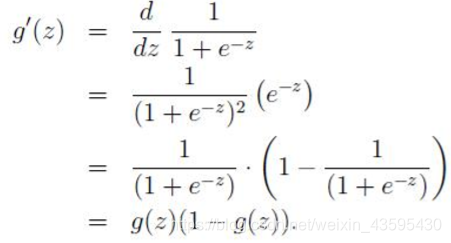
即先对特征线性求和（线性回归:h(x)=h1x1+h2x2+…+hnxn=h转置x)，再通过g(z)作为假设函数进行预测，g(z)可以将连续值映射到0-1之间,逻辑回归用于处理0/1问题，也就是预测结果属于0或者属于1的二值分类问题，根据属于0或者属于1的0-1的概率的大小判断属于哪一类。

也可以写成：

当y=1或y=-1时，分别等于上面的公式。
对于训练数据集，训练数据x={x1,x2,x3,…,xm}和对应的分类标签y={y1,y2,…ym},假设m个样本之间相互独立，那么极大似然函数为：

为了简化计算，取log似然函数为：

如何求其最大值，就要使用到梯度上升的方法，求最小使用梯度下降法，梯度下降法的讲解在这里

则更新迭代的规则就是：

我们希望极大似然函数越大越好，取负号就是越小越好，对其求平均，平均越小越好，则逻辑回归的损失函数为对数似然函数取平均，再取负号，使用梯度下降法不断逼近最优解。

逻辑回归怎么处理多分类问题:

1:修改逻辑回归的损失函数，将sigmoid函数转换成softmax函数构造模型解决多分类问题，softmax函数会有相同于类别数的输出，输出的只就是对应于样本属于哪个类别的概率，最终预测就是概率最大的值对应的类别。

2:对每一个类别都建立一个二分类器，本类别的样本的标签对应0，其他的分类样本标签对应1，则有多少的类别就建立多少的逻辑回归分类器。