作为机器学习算法中比较基础的LR算法,其在多个领域发挥着重要的作用,下面我们就来对其算法原理以及特点做一下总结。
Logistic Regression 基本原理
LR算法是典型的判别模型,即给定数据x,要求概率P(y|x)。假设我们有m个样本点集合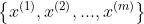 ,对应的标记为
,对应的标记为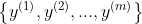 。
。
1. LR的二分类算法
我们假定给定数据x和模型参数 ,标记y服从伯努利分布,即
,标记y服从伯努利分布,即 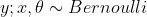 。因为我们做的是二分类,所以这个假设是非常直观的,但伯努利参数是多少?也就是当y=1的时候,p(y=1|x)是多少?下面的一个假设解决这个问题,它是基于GLM(广义线性模型,这里不做讨论)的,即:
。因为我们做的是二分类,所以这个假设是非常直观的,但伯努利参数是多少?也就是当y=1的时候,p(y=1|x)是多少?下面的一个假设解决这个问题,它是基于GLM(广义线性模型,这里不做讨论)的,即:

这里g是sigmoid函数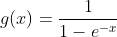 ,上面的式子也可以表达为
,上面的式子也可以表达为
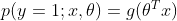
现在我们为每个样本的概率建立了模型,利用MLE(最大似然法),就可以求取相关参数 。对于似然函数log likelihood
。对于似然函数log likelihood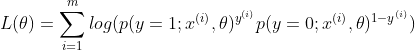 ,求
,求 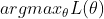 。我们首先可以求其解析解,另外,也可以通过梯度下降(当然这里是要求最大值,所以是梯度上升)的方法求取参数(本问题中L是关于
。我们首先可以求其解析解,另外,也可以通过梯度下降(当然这里是要求最大值,所以是梯度上升)的方法求取参数(本问题中L是关于 的凸函数,所以可以找到全局最优解)。本文讨论第二种方法,梯度下降法关键是要求出
的凸函数,所以可以找到全局最优解)。本文讨论第二种方法,梯度下降法关键是要求出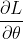 :
:

为表达方便上式中用 代替
代替 。
。
大家注意到,如果训练样本很大,即m是个非常大的数字,那么梯度下降法的每一步都会消耗很大的计算资源,有没有一种计算方便的改进算法呢?这就是随机梯度下降,同样这里也不做详述。
2. LR的多分类算法
和二分类情况类似的, 我们仍然可以假设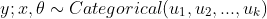 。不同的是这里y不再是0或者1,而是一个向量,例如样本隶属于第二分类,则
。不同的是这里y不再是0或者1,而是一个向量,例如样本隶属于第二分类,则![y = [0,1,0,...,0]](https://i-blog.csdnimg.cn/blog_migrate/588dfec614e48455e71914675cf3de5b.gif) 。我们仍然对模型做基于GML上的假设,
。我们仍然对模型做基于GML上的假设,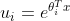 ,即每个类别i都有自己的参数
,即每个类别i都有自己的参数:
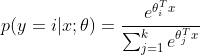
仔细观察,你会发现这是一个softmax函数!该模型的对数似然函数为

这样,我们依然可以用梯度下降或者随机梯度下降解决该问题。
总结
我们来看下逻辑回归算法的特点:
1. 算法简单容易理解,训练速度快,虽然其基于最大似然法容易过拟合,但通过正则化可以解决该问题。
2. 逻辑回归参数比较少,调节起来很方便。
3. 逻辑回归属于线性分类器,对于结构比较复杂且数据量比较大的的数据,我们一般不使用。
























 967
967

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








